字符串
用数值模拟非数值，比如ASCII码表
string：由零个或多个字符组成的有限序列
字符串的存储结构和线性表一样，也分顺序存储和链式存储，习惯上还是用顺序表。
子串匹配：
Brute Force 算法
朴素的模式匹配方法，按字符依次匹配，一个文本串s和一个模式串p，查找p在s中的位置，最坏时间复杂度是O(M*N)
假设当前匹配到 s[i] 和 p[j]，则：
1. 若 s[i] == p[j]，当前字符匹配成功，i++, j++
2. 若 s[i] != p[j]，当前字符匹配失败，i = i-(j-1) 回溯，j = 0 重置
但文本串存在不必要的回溯，问题实际是由模式串决定的。
KMP算法
保持 i 不回溯，通过修改 j 的位置，让模式串尽量地移动到有效的位置。给模式串p添加一个next数组，指导模式串p下一步回溯到第几个元素去进行下一轮的匹配。
假设当前匹配到 s[i] 和 p[j]，则：
若 j = -1 或者当前字符匹配成功（s[i] == p[j]），都令 i++，j++，继续匹配下一个字符；
若 j != -1 且当前字符匹配失败（s[i] != p[j]），则令 i 不变，j = next[j]。即，失配时，模式串p相对于文本串s向右移动了 j - next [j] 位。也即，失配时，p向右移动的位数 = 失配字符所在位 - 失配字符所在位对应的next值。
def KMPSearch(s, p):
i = 0 # 文本串的cursor
j = 0 # 模式串的cursor
while i < len(s) and j < len(p):
if j ==-1 or s[i] == s[j]:
i += 1
j += 1
else:
j = next[j] # 模式串回退j-next[j]位
if j == len(p):
return i-j
else:
return -1
next 数组的取值方式：
(1) 当 j = 0 时，next[j] = -1
(2) 当 0<k<j 且'p0...pk-1' == 'pj-k...pj-1' ，next[j] = max{k} (最大相同前缀后缀长度)
(3) 其他情况，next[j] = 0
例如给定模式串'abaabcac'，对应的next的数组为 next = [-1, 0, 0, 1, 1, 2, 0, 1]
如何求next数组？
假设已知 next [j] = k，那么有 'p0...pk-1' == 'pj-k...pj-1'。
1. 若 pj == pk ，next[j+1] = k+1 ；
2. 若 pj != pk , 失配，要去寻找更短的相同前缀后缀。换句话说，现在是p[k]和p[j]失配，那么k要回溯到next[k]（根据next数组的定义），这也就是一个自我匹配的过程：'p0...pk'去匹配'p0...pj' 且失配的情况。
j 表示后缀结束的位置，k表示前缀结束的位置，
next = [-1] * len(p)
def getNext(p):
j = 0
k = -1
next[0] = -1
while j < len(p) - 1:
if k == -1 or p[j] == p[k]:
k += 1
j += 1
next[j] = k # 如果p[j]等于p[k]，说明p[j+1]之前的最大相同前缀后缀长度为k，即next[j+1]=k+1
else:
k = next[k] # 如果不等于，说明要去找更短的前缀，也就是k要回溯。换句话说，p[k]和p[j]失配，k要回溯到next[k]
next数组的优化：
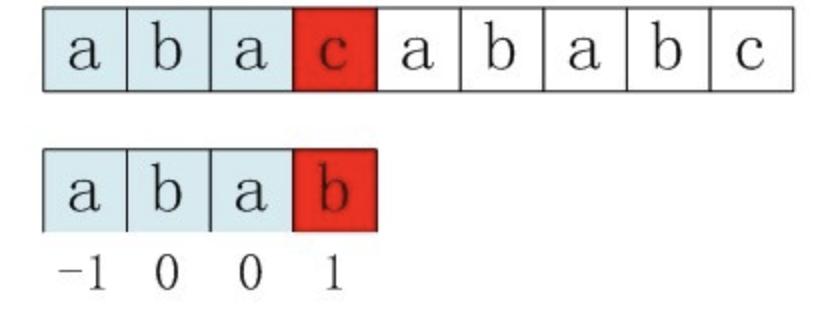
s[3] 和p[3]失配，j要回退j-next[j]=3-1=2位，即j = next[3] = 1
j回退两位之后p[1]和s[3]又失配，问题出在哪？ —— 不该出现 p[j] == p[next[j]]，因为如果这样话，一定是又失配的情况。所以如果出现了这种情况，就继续回溯。
next = [-1] * len(p)
def getNext(p):
next[0] = -1
k = -1
j = 0
while j < len(p) - 1:
if k==-1 or p[j] == p[k]:
k += 1
j += 1
if p[j] !=p[k]:
next[j] = k
else:
next[j] = next[k] # 当出现p[j] == p[next[j]] 时继续向后回溯
else:
k = next[k]
