递归 & 回溯 & 分治 & 贪心

递归 Recursion

通过函数体来进行的循环，一种编程技巧。倒着思考，看到问题的尽头。思路简单但效率低（建立函数的副本，消耗大量时间和内存）。递归是分治和动态规划的基础，而贪心是动态规划中的一种特殊情况（局部最优也是全局最优）。

终止条件（最简子问题的答案） + 自身调用（解决子问题），不要试图去搞清楚函数内部如何实现的，就先认为它可以实现这个功能。

比如，遍历一颗树

def traverse(root):
    if root is None:
        return
    for child in root.children:
        traverse(child)

　　

 

计算n阶乘，递归实现。

def Factorial(n):
    if n <= 1:   # 终止条件
        return 1
    return n*Factorial(n-1)

 

层层深入再回溯：

 

 

递归的代码模板：

def recursion(level, param1, param2, ...):
    # recursion terminator
    if level > MAX_LEVEL:
        print_result
        return 
    
    # process logic in current level
    process_data(level, data, ...)
    
    # drill down
    recursion(level + 1, p1, ...)

    # reverse the current level status if needed
    reverse_state(level)

　　

有些情况下递归处理问题是高效的，比如归并排序。但有些情况下，非常低效。比如斐波那契数列，显然递推是简单快速的，但如果非要递归但话也可以，低效。

 

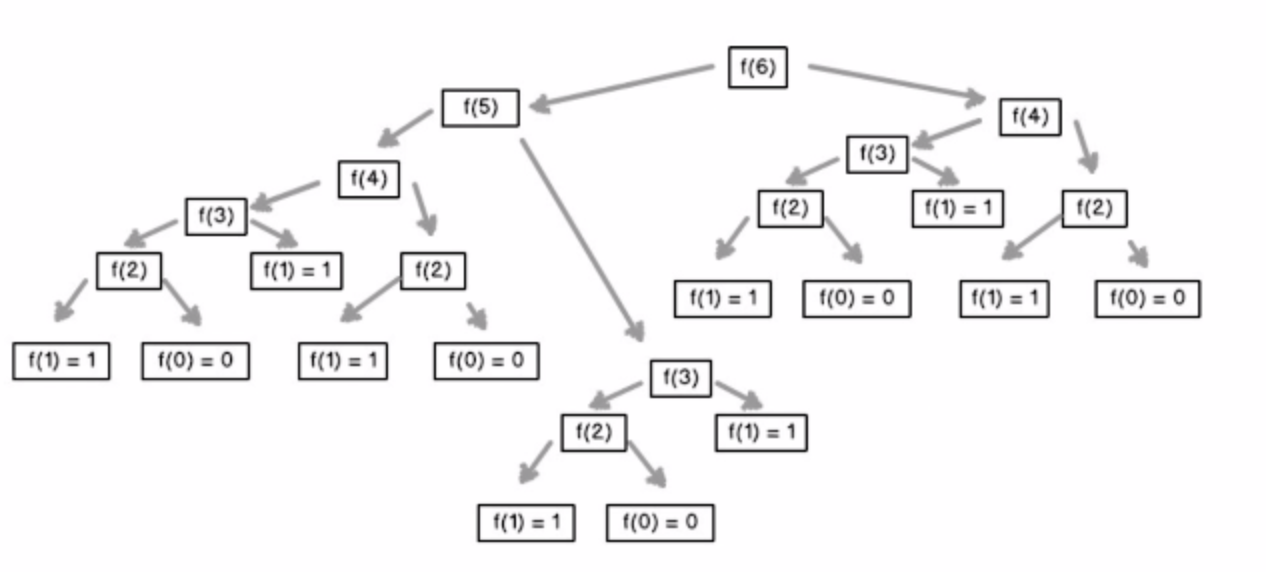
Fibonacci数列，函数调用自身，注意递归的停止条件。分为调用和回溯两个阶段。

但是过程中存在大量重复计算，递归效率并不高。（因为存在重复的子问题，可以用判重或记录结果）

# 递归
class Solution:
    def fib(self, N: int) -> int:
        if N <= 1:
            return N
        return self.fib(N-1) + self.fib(N-2)

# 迭代
class Solution:
    def fib(self, N: int) -> int:
        if N <= 1:
            return N
        tmp1 = 0
        tmp2 = 1
        for i in range(2, N+1):
            res = tmp1 + tmp2
            tmp1 = tmp2
            tmp2 = res
        return res

 

 

任意长度的字符串反向，递归实现

# 需要额外存储空间
def reverseStr(string):
    if string == None or len(string) == 0:
        return None
    if len(string) == 1:
        return string
    return reverseStr(string[1:])+string[0]

#leetcode，O(1)额外空间，原地修改。双指针
class Solution:
    def reverseString(self, s: List[str]) -> None:
        """
        Do not return anything, modify s in-place instead.
        """
        if s == None or len(s) <= 1:
            return None
        i, j = 0, len(s)-1
        while i<j:
            s[i], s[j] = s[j], s[i]
            i += 1
            j -= 1
        return

# 超时的递归解法
class Solution:
    def reverseString(self, s: List[str]) -> None:
        """
        Do not return anything, modify s in-place instead.
        """
        if s == None or len(s) <= 1:
            return None
        cur = s.pop(0)
        self.reverseString(s)
        s.append(cur)

 

汉诺塔问题：

def move(n, a, b, c):
    """n个盘子从a借助b移动到c上"""
    if n==1:
        print(a+'->'+c)
    else:
        move(n-1, a, c, b)
        move(1, a, b, c)
        move(n-1, b, a, c)

 

回溯 backtrack

回溯算法可以抽象理解为一个N叉树的遍历，比如斐波那契数列可以理解成一个二叉树，而零钱兑换的例子就是一个N叉树。

# 二叉树遍历
def traverse(root):
    if root is None:
        return
    # 前序代码在这
    traverse(root.left)
    # 中序代码在这
    traverse(root.right)
    # 后序代码在这

# N叉树遍历
def traverse(root):
    if root is None:
        return
    for child in root.childen:
        # 前序代码在这
        traverse(child)
        # 后序代码在这

　　

回溯的代码模板：

def backtrack(choiceList, track, answer):
    """choiceList, 当前可以进行的选择列表
        track, 决策路径，即已经作出的一系列选择
        answer, 储存符合条件的决策路径
    """
    if track is OK:
        answer.add(track)
    else:
        for choice in choiceList:
            # choose: 选择一个choice 加入track
            backtrack(choices, track, answer)
            # unchoose: 从track中撤销上面的选择

　　

全排列问题：给定一个没有重复数字的序列，返回其所有可能的全排列。

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        if not nums:
            return[[]]
        
        ans = []
        
        def backtrack(nums, track):
            nonlocal ans
            if not nums:
                ans.append(track)
            else:
                for i in range(len(nums)):
                    # track加入当前选的nums[i], 下一层nums[i]也不能选了
                    backtrack(nums[:i]+nums[i+1:], track+[nums[i]])
                    # track自然的回退了，因为没有真的append上去
        
        backtrack(nums, [])
        return ans

　　

子集：给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。解集不能包含重复的子集。

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        ans = []
        def backtrack(nums, track):
            nonlocal ans
            ans.append(track)  # 每次都记录track
            for i in range(len(nums)):
                backtrack(nums[i+1:], track+[nums[i]])
        backtrack(nums, [])
        return ans

　　

八皇后问题：

如何能够在 8×8 的国际象棋棋盘上放置八个皇后，使得任何一个皇后都无法直接吃掉其他的皇后？为了达到此目的，任两个皇后都不能处于同一条横行、纵行或斜线上。八皇后问题可以推广为更一般的n皇后摆放问题：这时棋盘的大小变为n×n，而皇后个数也变成n。当且仅当 n = 1 或 n ≥ 4 时问题有解。  

 

当在棋盘上放置了几个皇后且不会相互攻击。但是选择的方案不是最优的，因为无法放置下一个皇后。此时该怎么做？回溯：回退一步，来改变最后放置皇后的位置并且接着往下放置。如果还是不行，再回溯。

一行只可能有一个皇后且一列也只可能有一个皇后。这意味着没有必要再棋盘上考虑所有的方格。按行往下找皇后，对于每个皇后的位置只需要按列循环即可。对于所有的主对角线有：行号 - 列号 = 常数，对于所有的次对角线有 行号 + 列号 = 常数。

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        def could_place(row, col):
            # row这一行是没有放置过的行，要检查col这一列、(row,col)所占两条对角线有没有被放置过，如果都没有，(row,col)可以放皇后
            return not (cols[col]+hill_diagonals[row-col]+\
                        dale_diagonals[row+col]) 
        
        def place_queen(row, col):
            queens.add((row, col))  # 放皇后，记录位置，标记列和两对角线
            cols[col] = 1
            hill_diagonals[row-col] = 1
            dale_diagonals[row+col] = 1
        
        def remove_queen(row, col):
            queens.remove((row, col))  # 移除皇后，清空列和两对角线的标记
            cols[col] = 0
            hill_diagonals[row-col] = 0
            dale_diagonals[row+col] = 0
        
        def add_solution():
            # 如果找到一个解，按要求记录下来
            solution = []
            for _, col in sorted(queens):
                solution.append('.'*col + 'Q' + '.'*(n-col-1))
            output.append(solution)
        
        def backtrack(row):
            # 从第一行row=0开始放置皇后，放到n-1行
            for col in range(n):  # 对于确定的row，遍历所有列col
                if could_place(row, col):
                    place_queen(row, col)  # 如果(row, col)可以放皇后，就放
                    if row == n-1:  # 如果已经放了最后一个，说明找到一个解
                        add_solution()
                    else:  # 没有放到最后一个的话
                        backtrack(row+1)  # 去找row行之后所有可能的放置解法
                    remove_queen(row, col)  # 不管是哪种情况都要回溯，移除当前皇后，进入(row, col+1)的情况
            
        cols = [0] * n
        hill_diagonals = [0] * (2 * n -1)
        dale_diagonals = [0] * (2 * n -1)
        queens = set()
        output = []
        backtrack(0)
        return output

  

 

分治 Divde & Conquer

将问题分成几个小模块，逐一解决。典型的递归结构。分治可以高效率解决的，是没有中间结果（没有所谓的重复计算）的问题。　（适合的解决方法：动态规划、子问题记忆）

 

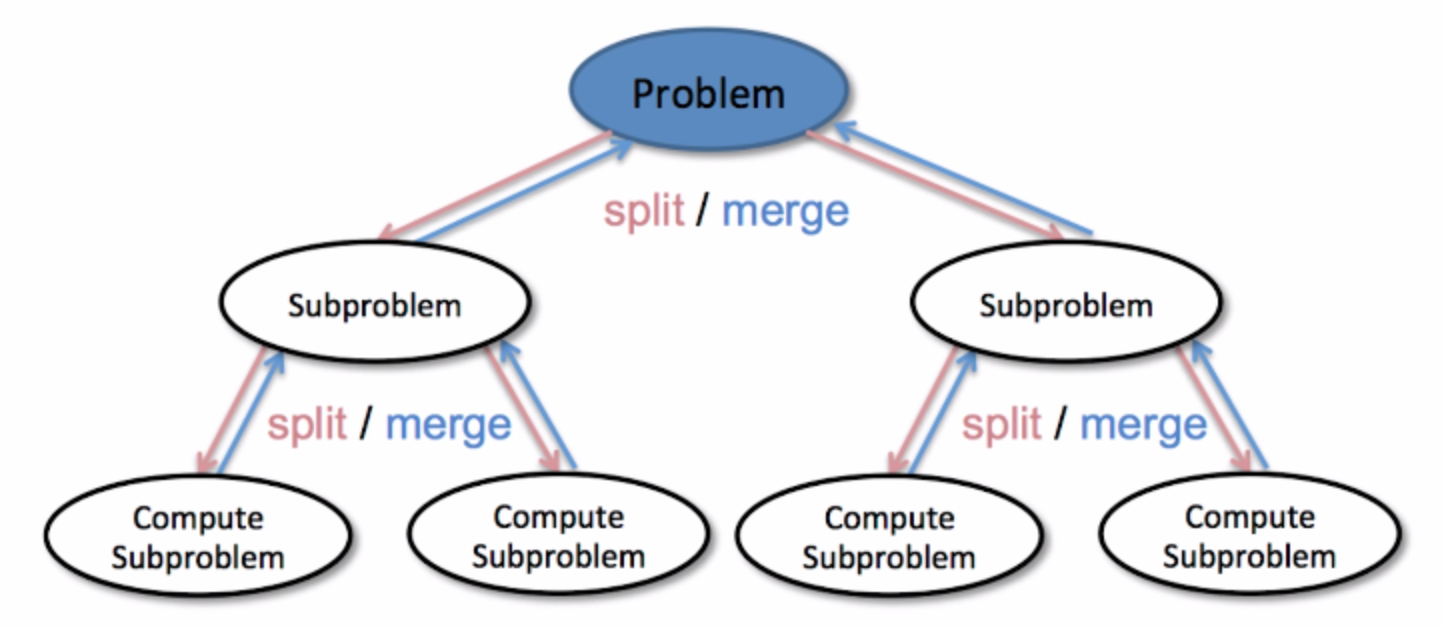
给定一个字符串，将小写字母变为大写。循环或者递归都可以。分治的做法：

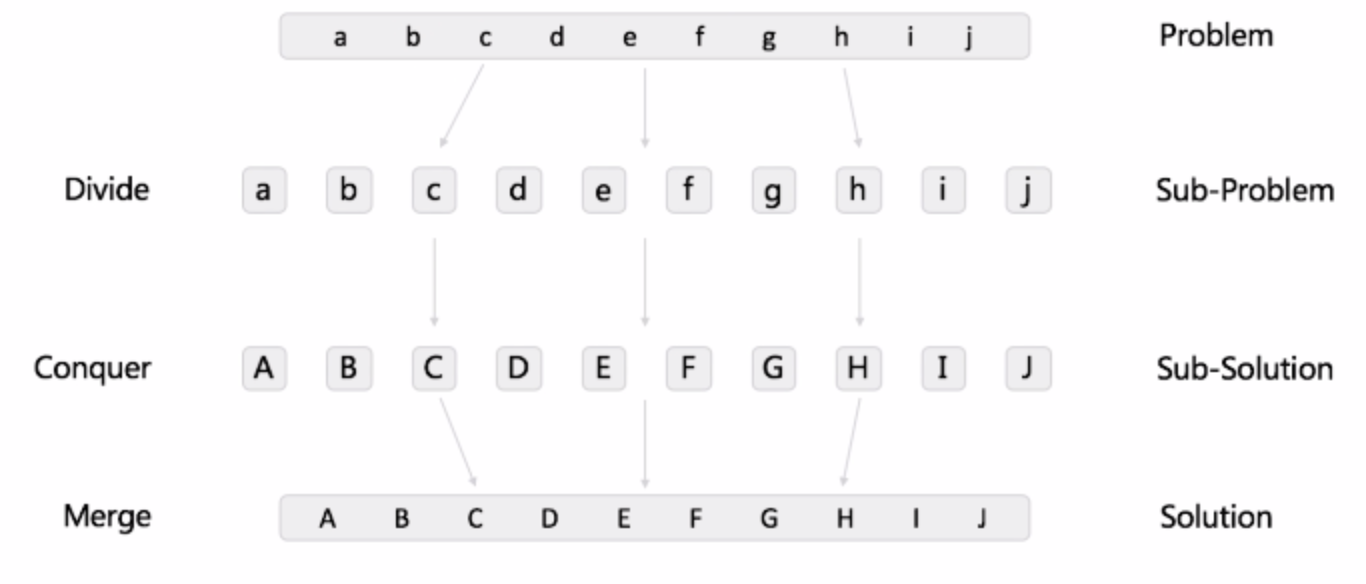
子问题互不相关，可以并行计算。

 

典型的分治思想，归并排序。将数组分解最小之后，把n个记录看成是n个有序的子序列，每个子序列长度为1。然后两两归并，得到ceil(n/2)个长度为2或者1的有序子序列，再两两归并...，如此重复直到得到长度为n的有序序列为止。

用递归实现的话就很简洁，直接左右两边递归的归并排序，再merge左右两边就行了。

def merge_sort(alist):
    if len(alist) <= 1:
        return alist
    # 二分分解
    num = len(alist)//2
    left = merge_sort(alist[:num])
    right = merge_sort(alist[num:])
    # 合并
    return merge(left,right)

　　

剩下的细节无非就是写一下如何合并两个有序数组，双指针同时向后扫，小的就放进结果指针后移，大的就指针不动。

def merge(left, right):
    '''合并操作，将两个有序数组left[]和right[]合并成一个大的有序数组'''
    #left与right的下标指针
    l, r = 0, 0
    result = []
    while l<len(left) and r<len(right):
        if left[l] < right[r]:
            result.append(left[l])
            l += 1
        else:
            result.append(right[r])
            r += 1
 
    if l < len(left):
        result += left[l:]
    elif r < len(right):
        result += right[r:]
    return result

　　

完事了。用迭代写的话要利用mod的技巧来操作索引，还是比较繁琐的。代码放到排序https://www.cnblogs.com/chaojunwang-ml/p/11296423.html 中了。

 

分治的代码模板：

def divide_conquer(problem, param1, param2, ...):
    # recursion terminator
    if problem is None:
        print_result
        return
    
    # prepare data
    data = prepare_data(problem)
    subproblems = split_problem(problem, data)
    
    # conquer subproblems
    subresult1 = divide_conquer(subproblems[0], p1, ...)
    subresult2 = divide_conquer(subproblems[1], p1, ...)
    ...
    
    # process and generate the final result
    result = process_result(subresult1, subresult2, ...)
    

　　

 

二分搜索，思路很简单，但细节很蛋疼。

# 最普通的情况，规定有序数组不重复
class Solution:
    def search(self, nums: List[int], target: int) -> int:
        if nums == None or len(nums) == 0:
            return -1
        low = 0
        high = len(nums) - 1
        while low <= high:   # 双端闭区间[low, high]查找 
            mid = (low + high) // 2
            if nums[mid] == target:
                return mid
            elif nums[mid] > target:
                high = mid - 1
            elif nums[mid] < target:
                low = mid + 1  
        return -1

# 寻找左侧边界的二分搜索。初始化 right = nums.length，决定了「搜索区间」是 [left, right)，所以决定了 while (left < right)，同时也决定了 left = mid + 1 和 right = mid
# 因为需找到 target 的最左侧索引，所以当 nums[mid] == target 时不要立即返回，而要收紧右侧边界以锁定左侧边界。

def search(nums, target):
        if nums == None or len(nums) == 0:
            return -1
        low = 0
        high = len(nums)
        while low < high:   # [low, high) 上搜索
            mid = (low + high) // 2
            if nums[mid] == target:
                high = mid   # 找到target之后不要立即返回，缩小搜索区间上界，在[low, mid)中继续搜索，锁定左侧边界low
            elif nums[mid] > target:
                high = mid
            elif nums[mid] < target:
                low = mid + 1 
        if low == len(nums): # target 比所有数都大
            return -1
        return low if nums[low] == target else -1  # 如果找到，low应该指向左侧边界

# 寻找右侧边界的二分搜索
def search(nums, target):
        if nums == None or len(nums) == 0:
            return -1
        low = 0
        high = len(nums)
        while low < high:   # [low, high) 上搜索
            mid = (low + high) // 2
            if nums[mid] == target:
                low = mid + 1   # 找到target之后不要立即返回，缩小搜索区间下界，在[mid+1, high)中继续搜索，锁定右侧边界high-1
            elif nums[mid] > target:
                high = mid
            elif nums[mid] < target:
                low = mid + 1 
        if low == len(nums): # target 比所有数都大
            return -1
        return low-1 if nums[low-1] == target else -1  # 若找到，最后low == high，右侧边界在 high-1

# 递归实现二分搜索，和迭代是一样的，因为没有重叠子问题
class Solution:
    def search(self, nums: List[int], target: int) -> int:
        if nums == None or len(nums) == 0:
            return -1
        return self.recursiveSearch(nums, 0, len(nums)-1, target)
    
    def recursiveSearch(self, nums, low, high, target):
        if low > high:  # 双端闭区间搜索
            return -1
        mid = (low+high)//2
        if nums[mid] == target:
            return mid
        elif nums[mid] > target:
            return self.recursiveSearch(nums, low, mid-1, target)
        elif nums[mid] < target:
            return self.recursiveSearch(nums, mid+1, high, target)
        return -1

 

 

贪心 Greedy

对问题求解的时候，总是做出在当前看来最优的选择。但处处做贪心，总体未必是最优的。

适用贪心的场景：问题能够分解成子问题来解决，子问题的最优解能够递推到最终问题的最优解。这种子问题最优解称为最优子结构。

贪心和动态规划的区别在于，它对每个子问题的解决方案都做出选择，不能回退。而动态规划会保存以前的运算结果，并根据以前的结果对当前进行选择，有回退功能。贪心可以看作是动态规划的一个特例。

 

手里有面额20、10、5、1元的四种纸币，问要凑够36元最少需要多少张。

每次先选最大面额的，不能选了再选次大的；...

 

经典贪心，Interval Scheduling（区间调度问题），算出给定的一组[start, end]区间中最多有几个互不相交的区间。例如 intvs = [[1, 3], [2, 4], [3, 6]]，最多有两个区间互不相交。边界相同不算相交。

1. 从区间集合中选出 end 最小的区间x；2.把所有和这个区间相交的区间从 intvs 中删除；3. 重复1.2. 直到intvs 为空。

可以先排个序，这样如果一个区间不和 x 相交的话，start必须要大于等于x_end

class Solution:
    def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
        if not intervals:
            return 0
        n = len(intervals)
        intervals.sort(key=lambda x: x[1])  # 先按 end 排序
        
        count = 1  # 至少一个区间不相交
        x_end = intervals[0][1]
        for i in range(1, n):
            if intervals[i][0] >= x_end:  # 如果一个区间的start大于等于x_end，那么区间必然不相交x，计数并且更新x即可
                count += 1
                x_end = intervals[i][1]
        return n-count

　　

用最少的箭头射爆气球

在二维空间中有许多球形的气球。对于每个气球，提供的输入是水平方向上，气球直径的开始和结束坐标。由于它是水平的，所以y坐标并不重要，因此只要知道开始和结束的x坐标就足够了。开始坐标总是小于结束坐标。平面内最多存在104个气球。

一支弓箭可以沿着x轴从不同点完全垂直地射出。在坐标x处射出一支箭，若有一个气球的直径的开始和结束坐标为 xstart，xend， 且满足  xstart ≤ x ≤ xend，则该气球会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后，可以无限地前进。我们想找到使得所有气球全部被引爆，所需的弓箭的最小数量。

这题和区间调度问题一摸一样，如果最多有n个不重叠区间，就至少需要n个箭头射爆气球。