栈和队列
栈
一种重要的线性结构;后进先出。特殊的线性表,只能在表尾进行插入(push)和删除(pop)操作。 表尾称为栈顶(top),表头称为栈底(bottom)。一般用顺序表实现。
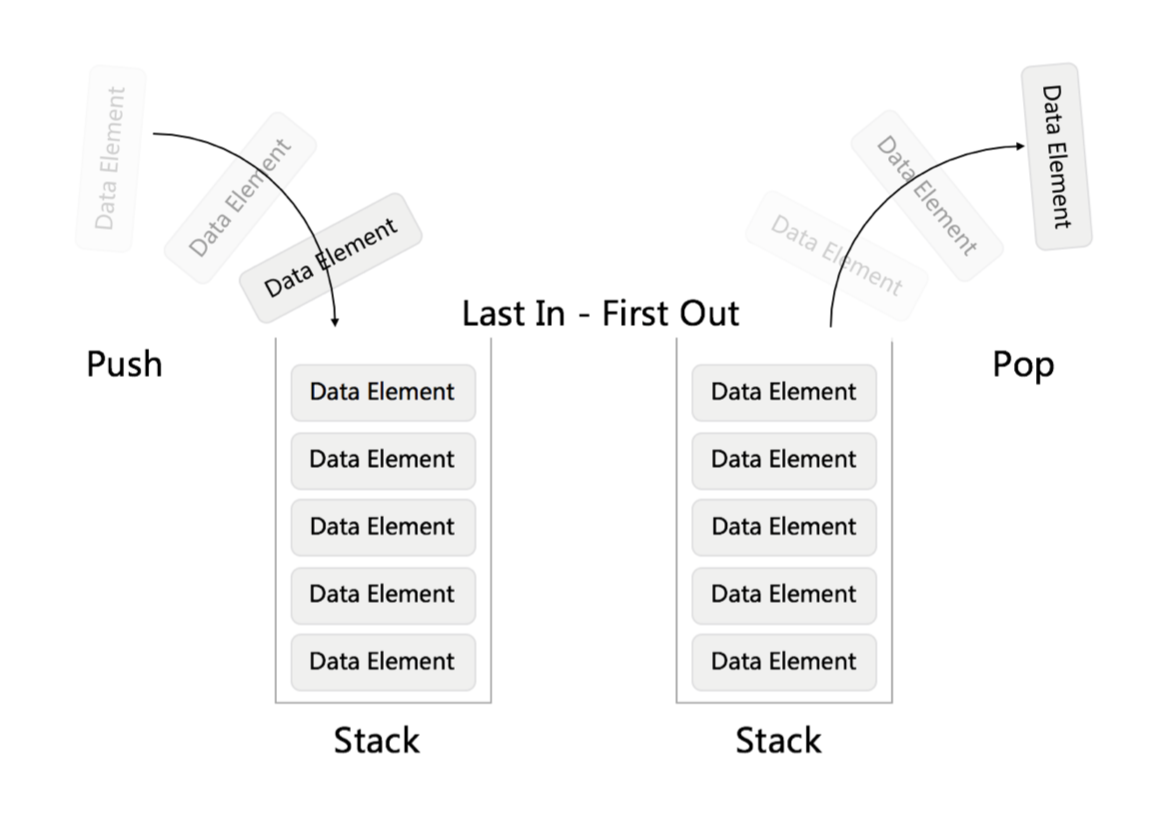
清空一个栈:s->base = s->top
销毁一个栈:释放其所占的物理内存空间。
for(i=0, i<s->stackSize) {free(s->base); s->base++}
s->base = s->top = NULL; s->stackSize = 0
用栈实现二进制转十进制
def Bin2Dec(BinStrs):
strStack = []
for elem in BinStrs:
strStack.append(elem)
DecRes = 0
n = 0
while strStack:
DecRes += eval(strStack.pop())*(2**n)
n += 1
return DecRes
BinInputs = input('Binary input:')
print('Decade output:', Bin2Dec(BinInputs))
栈的链式存储结构,将栈顶放在单链表的头部,即栈顶指针和单链表的头指针合二为一。
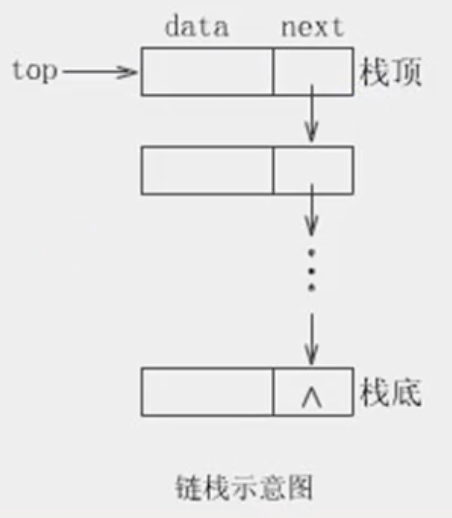
逆波兰表达式RPN:利用栈来进行运算的数学表达式。(中缀表达式转换为后缀表达式)
class Solution:
def evalRPN(self, tokens: List[str]) -> int:
Stack = []
operations = {'+','-','*','/'}
# 遇到操作符就pop出两个元素进行操作,结果再push进栈
for token in tokens:
if token in operations:
right = Stack.pop()
left = Stack.pop()
tmp = 0
if token == '+':
tmp = left + right
elif token == '-':
tmp = left - right
elif token == '*':
tmp = left*right
else: # 整除要判断正负性
if right*left > 0:
tmp = left//right
elif right*left < 0:
tmp = -(-left//right)
Stack.append(tmp)
else:
Stack.append(int(token))
return Stack.pop()
中缀表达式转换为后缀表达式:
1.遇到操作数,直接输出;
2.栈为空时,遇到运算符,入栈;
3.遇到左括号,将其入栈;
4.遇到右括号,执行出栈操作,并将出栈的元素输出,直到弹出栈的是左括号,左括号不输出;
5.遇到其他运算符’+”-”*”/’时,弹出所有优先级大于或等于该运算符的栈顶元素,然后将该运算符入栈;
6.最终将栈中的元素依次出栈,输出。
def middle2behind(expresssion):
result = [] # 结果列表
stack = [] # 栈
operations = {'+','-','*','/','(',')'}
for item in expression:
if item not in operations: # 数字直接输出
result.append(item)
else: # 如果是操作符
if len(stack) == 0: # 若栈空,直接入栈
stack.append(item)
elif item in '*/(': # 如果当前字符为*/(,直接入栈
stack.append(item)
elif item == ')': # 如果右括号则全部弹出(碰到左括号停止,左括号不输出)
t = stack.pop()
while t != '(':
result.append(t)
t = stack.pop()
# 如果当前字符为加减且栈顶为乘除,则开始弹出
elif item in '+-' and stack[-1] in '*/':
if stack.count('(') == 0: # 如果没有有左括号,全部弹出
while stack:
result.append(stack.pop())
else: # 如果有左括号,弹出到左括号为止
t = stack.pop()
while t != '(':
result.append(t)
t = stack.pop()
stack.append('(') # 左括号pop出来了,再补回去
stack.append(item) # 弹出操作完成后将‘+-’入栈
else:
stack.append(item)# 其余情况直接入栈(如当前字符为+,栈顶为+-)
# 栈中还有操作符不满足弹出条件,把栈中的东西全部弹出
while stack:
result.append(stack.pop())
# 返回字符串
return "".join(result)
单调栈:保持先进后出的栈特性,每次新元素入栈后,栈内的元素都保持有序。
处理Next Greater Element问题。给定一个数组a,返回一个等长数组b,b中存储a中相同索引的元素的下一个更大元素,如果没有就存-1。例如a=[2,1,2,4,3],返回b=[4,2,4-1,-1]。
暴力解,两层遍历O(n2),不写了。
单调栈,每个元素入栈一次,最多pop一次,O(n)。
def nextGreaterElement(nums):
if not nums:
return []
n = len(nums)
ans = [-1] * n
stack = [] # stack
for i in range(n-1, -1, -1): # nums中的元素倒着入栈,就正着出栈
while stack and stack[-1] <= nums[i]: # 只要栈顶元素不大于当前元素,就pop出去
stack.pop() # 所以stack始终被维护成一个从底到顶单调递减的栈
ans[i] = stack[-1] if stack else -1 # 栈顶元素是第一个比当前元素大的元素。按ans索引从后往前赋值
stack.append(nums[i]) # 当前元素入栈,等着和nums中i之前位置的元素比较
return ans
问题改为,返回一个数组,存的是每个元素距其Next Greater Element的距离。例如a=[2,1,2,4,3],返回b=[3,1,1,0,0]。
def distance_nextGreaterElement(nums):
if not nums:
return []
n = len(nums)
ans = [-1] * n
stack = [] # stack
for i in range(n-1, -1, -1): # nums中的元素倒着入栈,就正着出栈
while stack and nums[stack[-1]] <= nums[i]: # 只要栈顶索引对应的元素不大于当前元素,就把索引pop出去
stack.pop() # 所以stack始终被维护成一个索引对应值单调递减的栈
ans[i] = stack[-1] - i if stack else 0 # 栈顶元素是第一个比当前元素大的,按索引从后往前赋距离
stack.append(i) # 当前元素索引入栈
return ans
还是Next Greater Element问题,假设给定的数组是环形的。那么某个元素的Next Greater Element就有可能在它本身之前了。例如a=[2,1,2,4,3],返回b=[4,1,1,-1,4]。
可以直接在原数组后面再挂一个原数组,还用上面的思路求解。例如 [2,1,2,4,3, 2,1,2,4,3],结果为[4,2,4,-1,4, 4,2,4,-1,-1]取前一半即可。
或者直接用索引mod n的技巧模拟这种double数组的情况。
ef nextGreaterElement(nums):
if not nums:
return []
n = len(nums)
ans = [-1] * n
stack = [] # stack
# 假设数组长度翻倍了,还是从后往前
# 遍历后半部分求解的时候没有按循环数组取下一个大值,但在遍历到前半部分的时候就把正确结果覆盖了
# 相当于ans更新了两遍
for i in range(2*n-1, -1, -1):
while stack and stack[-1] <= nums[i % n]:
stack.pop()
ans[i % n] = stack[-1] if stack else -1
stack.append(nums[i % n]) # 索引 mod n 取到在nums中真实位置的值
return ans
队列
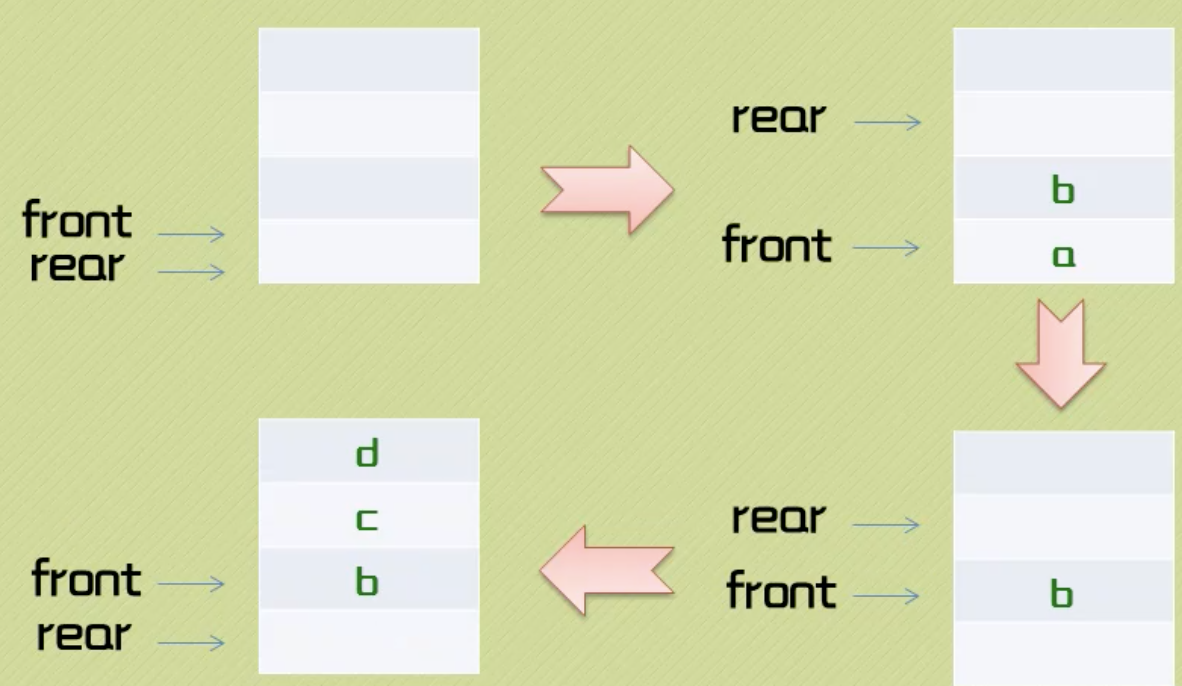
先进先出,可以用线性表或链表实现。一般用链表实现。队列头指针front指向头节点,队列尾指针rear指向尾节点。链表尾插头出。
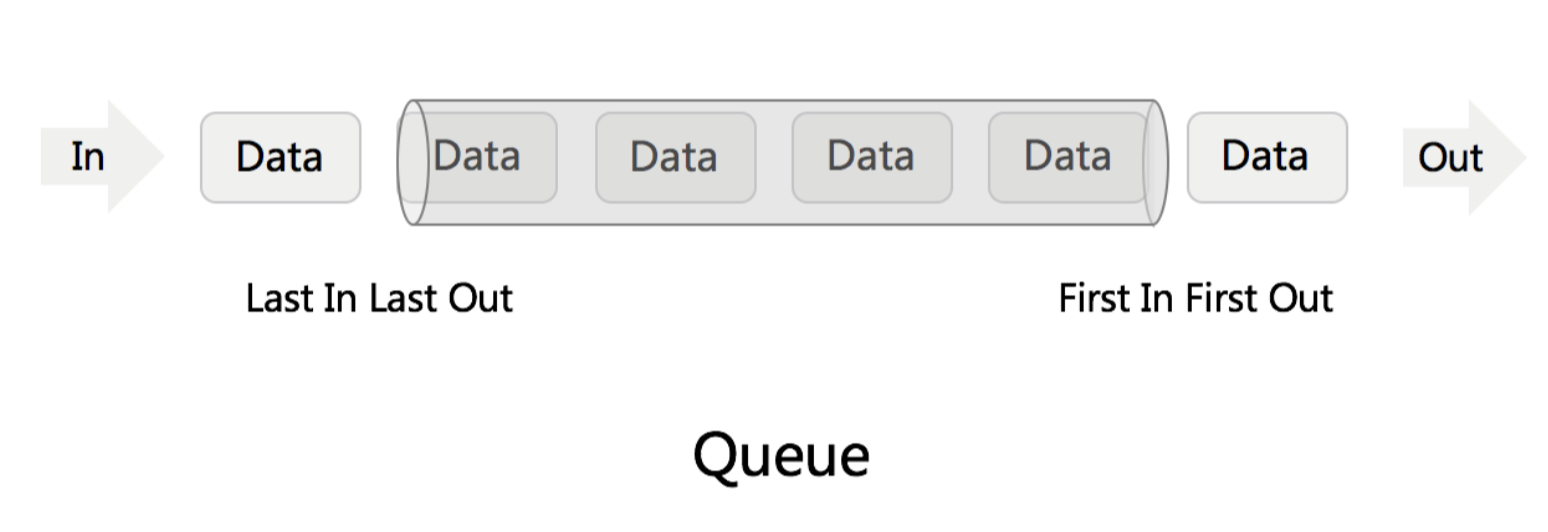
队列的顺序存储结构:循环队列解决假溢出。
还是用数组,其实只需要让 front 和 rear 不断加 1(插入改rear、弹出改front),如果超出了地址范围就从头开始(避免假溢出),直到 front 和 rear 相遇就满了。可以采取 mod 运算实现。
- (rear+1) % queueSize
- (front+1) % queueSize
双端队列:这种混合的线性数据结构拥有栈和队列各自拥有的所有功能。插入和删除操作的规律性需要由用户自己维持。

应用:判断回文字符
单调队列: 队列中元素单调递增或者递减。单调队列的 push 方法依然在队尾添加元素,但是要把前面比新元素小的元素都删掉。如果每个元素被加入时都这样操作,最终单调队列中的元素大小就会保持一个单调递减的顺序。
回顾一下leetcode 239 滑动窗口最大值。窗口滑动的过程中新增一个数又减少一个数,这时候最值的更新就不是那么快可以直接算,要重新遍历窗口中的所有数据。
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
if not nums:
return []
n = len(nums)
res = []
window = [] # 双端队列实现单调队列
for i in range(n):
if i >= k and window[0] <= i-k:
window.pop(0) # 从第二个窗口开始需要pop最左边滑出窗口的值
while window and nums[window[-1]] <= nums[i]: # 维护递减的单调队列
window.pop() # popright
window.append(i) # 新的值进来,此时window最左端就是当前窗口的最大值
if i >= k-1: # 从第一个窗口开始记录结果
res.append(nums[window[0]])
return res
优先队列:正常入队,按优先级出队。当插入或者删除元素的时候,元素会自动排序。实现机制为堆或者二叉搜索树。
大/小顶堆的性质就是每个父节点都大于等于/小于等于其子节点。维护堆的操作就是下沉和上浮。
特别的一点是,元素存储在数组里,数组的索引作为指针,注意第一个索引0空着不用。给定一个节点root,其孩子节点为2*root和2*root+1;同理给定一个root,其父节点为root//2。
大顶堆的常用操作为 insert 和 delMax;小顶堆的常用操作为 insert 和 delMin。
以大顶堆为例,如果一个节点的val比父节点的val大,需要上浮;如果小于其孩子节点,需要下沉。
伪代码
def swim(k):
while k > 1 and less(parent(k), k): # 如果浮到顶了就不用动了,如果k比其父节点大,把k换上去
exchange(parent(k), k)
k = parent(k)
def sink(k):
while left(k) <= N: # 沉到堆底就不用沉了
larger = left(k) # 假设左边节点较大
if right(k) <= N and less(larger, right(k)):
larger = right(k) # 如果右边节点存在且更大,就更新larger
if less(larger, k): # 和k比较,如果k比其孩子节点都大,不用下沉了
break
exchange(k, larger) # 否则的话往larger方向下沉k节点
k = larger
插入和删除
def insert(e):
N ++ # 先把元素放最后
pq[N] = e
swim(N) # 上浮到正确位置
def delMax()
Max = pq[1] # 堆顶最大
exchange(1, N) # 换到最后,删除
pq[N] = null
N --
sink(1) # 让pq[1]沉到正确位置
return Max
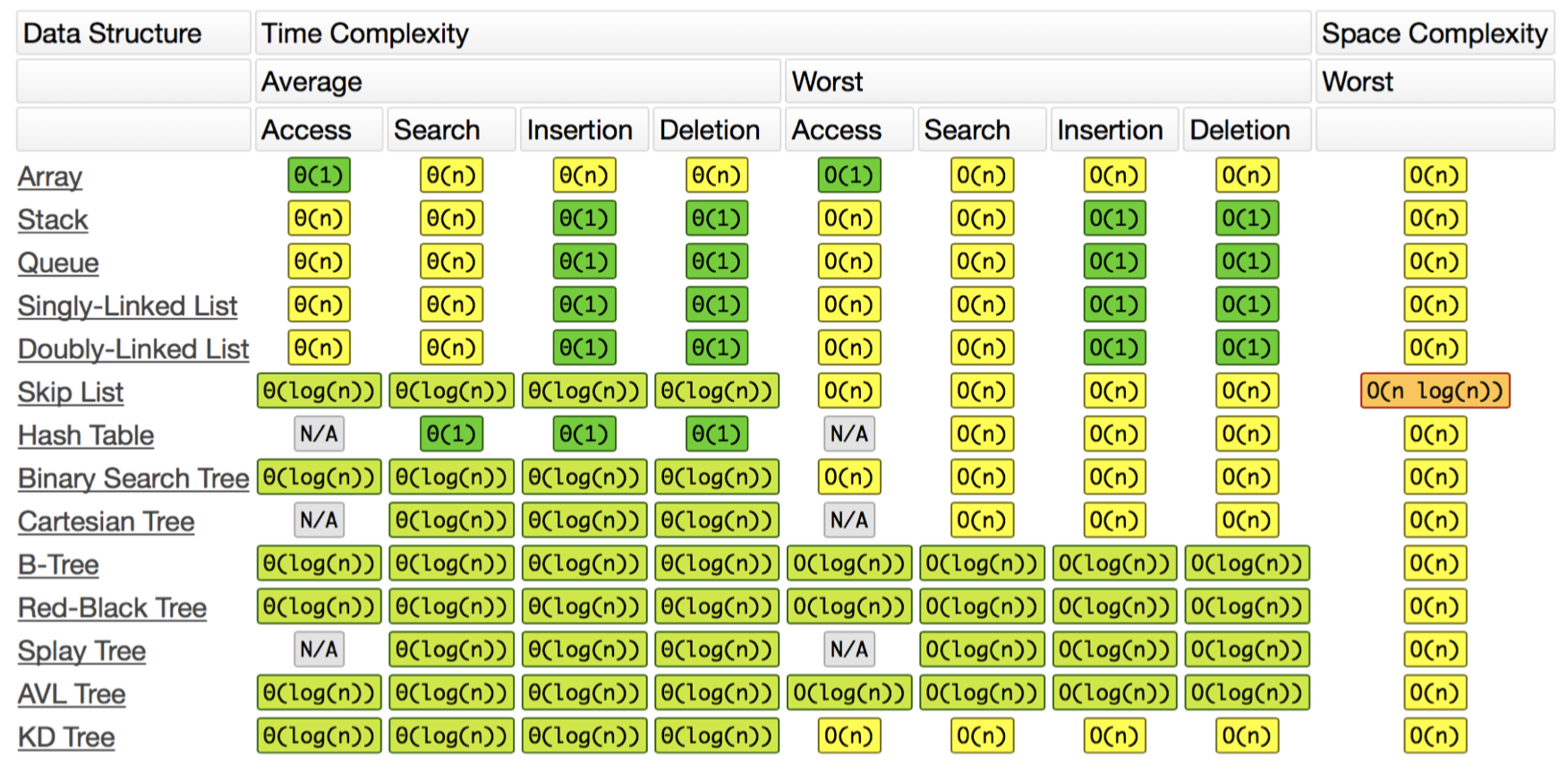
堆的各种实现形式及对应的操作效率

常用数据结构及其各种操作的时间复杂度