线性回归 Linear Regression

一、主要思想

在 L2-norm 的误差意义下寻找对所有观测目标值 Y 拟合得最好的函数 f(X) = W^TX 。

其中 y_i 是 scalar，x_i 和 W 都是 P 维向量（比实际的 x_i 多一维，添加一维 xi⁽⁰⁾ = 1，用于将偏置 b 写入 W 中）

1. 定义模型：f(X) = W^TX

2. 目标函数：L2-norm 损失（均方误差损失）

3. 寻优：梯度下降（迭代）或 最小二乘（解析解）

 

引入高维可以使得线性回归模型更加复杂，可以在 training data 上拟合的更好，但要考虑 overfitting ，真正关心的应该是模型在 testing data 上的效果

 

 

 

 

 

二、正则化

约束参数空间，改善过拟合

 

通过梯度下降来分析两种正则的区别（Hung-yi Lee） 

1. L1 正则的线性回归：Lasso

　　L1-norm regularization 让参数变小的机制，是每次都减去（if w >= 0）或者加上（if w < 0）一个值（即 λ*learning_rate），不管哪种情况，最后都是让参数往反方向变化。

 

等价于对参数 w 引入拉普拉斯分布先验。f(x | μ, b) = exp(-|x-μ| / b) / 2b

  

2. L2 正则的线性回归：Ridge

　　L2-norm regularization 的机制是每次在更新参数之前，都先直接乘上一个小于1的数。这样也是不管参数正负都会更接近0，但是L1 norm 中每次减掉的值是固定的，而 L2 norm 参数变小的速度跟其本身的大小相关。

小结：

　　1. 用 L1 正则得到的参数比较 sparse，有大的也有很接近 0 的；而 L2 正则就会使得所有的参数都接近 0 。

　　2. 使用正则化让参数变小会使得模型表示的函数更加平滑（对噪声不那么敏感，改善过拟合），但正则化程度也会使得损失函数太过于考虑W而原本的损失项影响很小，导致模型变差（最极端情况：就是一条水平线，啥都拟合不了）。所以正则化系数由小变大，存在一个令模型测试集表现由好至差的转折点。

　　3. 正则化项是不需要作用在偏置项上的，因为偏置只会上下平移函数不会影响平滑程度。

 

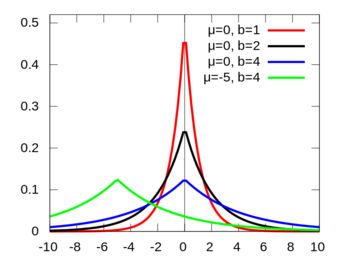
加上L2正则化的最小二乘估计  等价于  噪声 ε 为高斯（0，σ²）、参数 w 先验也为高斯（0, σ₀²）的最大后验估计

最小二乘法的解析解中 X^TX 不可逆怎么处理？

—— X^TX + λI （也正是L2正则的效果）

 

 

 

 

加入 L2 norm 正则化项会使得参数倾向于变小，进而使得模型表示的函数更加平滑。

为什么使得模型函数平滑一些会比较好？—— 使得模型输出对输入中的噪声不那么敏感。

 

过于平滑会怎样？—— 极端情况下最平滑就是一条水平线，那就啥都拟合不了，所以平滑程度太大会导致模型在测试集上表现差。

 

 

正则化项系数太大也不行，会导致 loss 太过于考虑 w 的项而过于弱化原本的损失函数项的影响。正则化项系数从小到大对模型的测试集表现的影响，会有一个从好至坏的转折点；而对训练集来说，误差随之总是越来越大的。

 

 

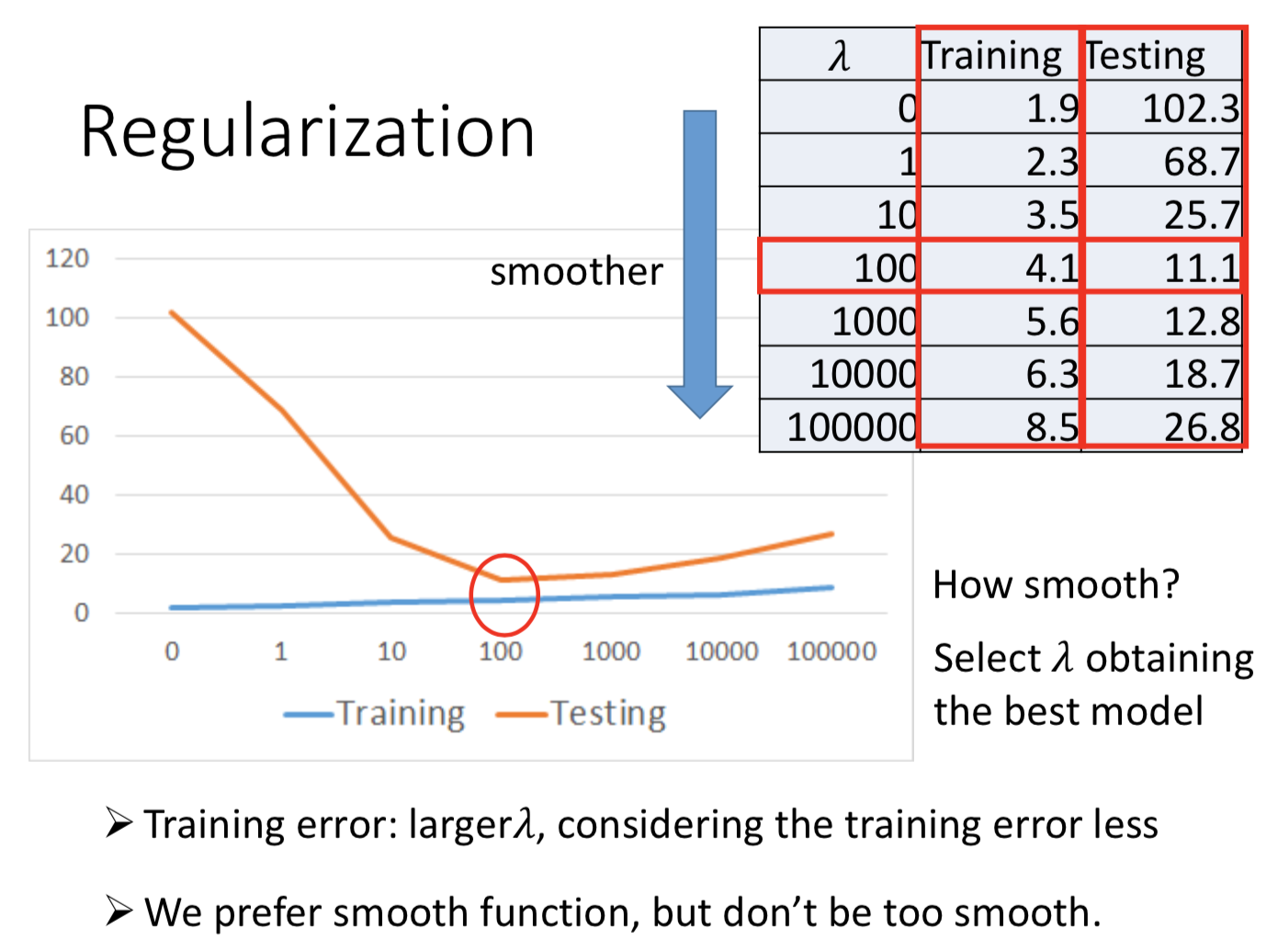
正则化不需要作用在 bias 上，因为偏置项和模型（映射函数）的平滑程度无关，只会上下平移函数。

 

 

三、从把误差分散到 P 维的角度考虑线性回归模型

把 f(X) 理解为 P 维向量 X 的线性组合 X·ß

任务：要在 X 所在的 P 维空间里找到一个离Y最近的 X·ß

显然是 Y 在这个 P 维空间的投影，所以 Y-X·ß 垂直于 X，直接求得解析解

 

 

四、从概率视角理解线性回归模型

随机变量 X 和 Y 分别表示样本和观测，令 Y = W^TX + ε，噪声 ε 服从高斯分布 N(0, σ²)

则 Y | W, X, ε 服从均值偏移 W^TX、方差不变的高斯分布 N(W^TX, σ²)

 

MLE：用极大似然估计来寻找参数 W 的值（令似然函数 P(Y | W, X, ε) 最大的 W）

　　　可以发现要 argmin 的函数和最小二乘估计中的平方误差损失函数一致

最小二乘估计 等价于 噪声为高斯的最大似然估计