深度学习基础课:最大池化层的后向传播推导
大家好~本课程为“深度学习基础班”的线上课程,带领同学从0开始学习全连接和卷积神经网络,进行数学推导,并且实现可以运行的Demo程序
线上课程资料:
加QQ群,获得ppt等资料,与群主交流讨论:106047770
本系列文章为线上课程的复盘,每上完一节课就会同步发布对应的文章
本课程系列文章可进入索引查看:
回顾相关课程内容
- 最大池化层的前向传播算法是什么?
为什么要学习本课
- 如何推导最大池化层的后向传播?
主问题:如何推导最大池化层的后向传播?
- 最大池化层的后向传播算法有哪些步骤?
答:只有一步:已知下一层计算的误差项,反向依次计算这一层的误差项
(因为这一层没有权重值,所以不需要计算这一层中的梯度)
主问题:如何反向计算误差项?

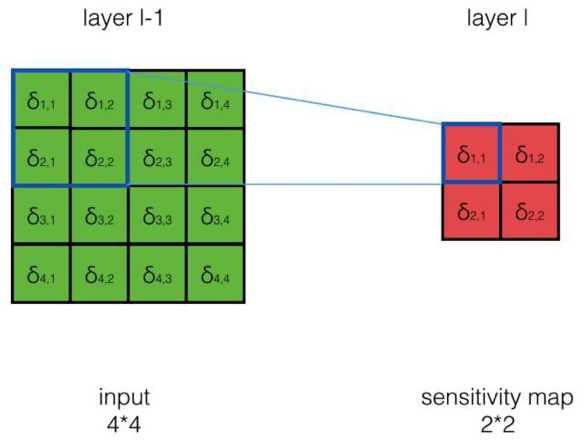
- 如何求\(\delta_{i,j}^{l-1} = \frac{dE}{dnet_{i,j}^{l-1}}\) = ?
答:我们先来考察一个具体的例子,然后再总结一般性的规律- 如何求\(\delta_{1,1}^{l-1} = \frac{dE}{dnet_{1,1}^{l-1}}\) = ?其中\(net_{1,1}^{l-1}对哪些net_{i,j}^l有影响?\)
答:

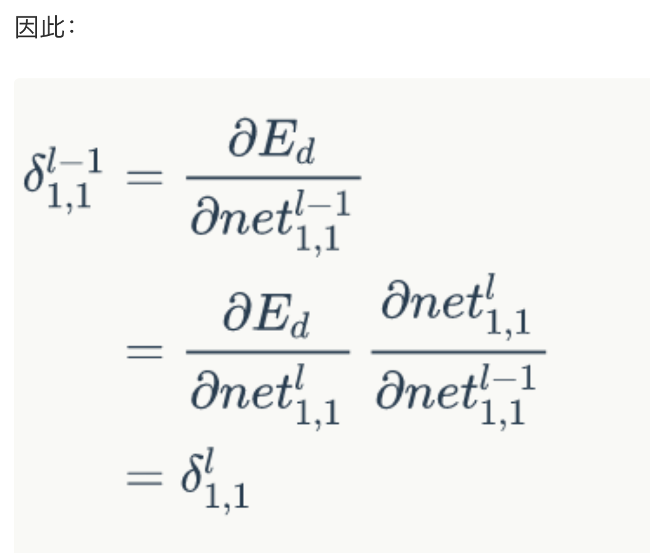
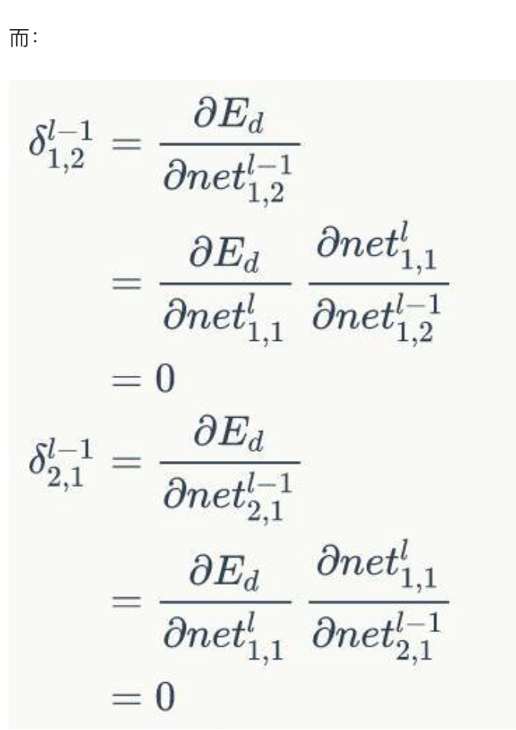
- 如何求\(\delta_{1,1}^{l-1} = \frac{dE}{dnet_{1,1}^{l-1}}\) = ?其中\(net_{1,1}^{l-1}对哪些net_{i,j}^l有影响?\)
\[\begin{aligned}
\delta_{2,2}^{l-1} &= \frac{dE}{dnet_{2,2}^{l-1}} \\
&= \frac{dE}{dnet_{1,1}^{l}} \frac{dnet_{1,1}^{l}}{dnet_{2,2}^{l-1}} \\
&= 0
\end{aligned}
\]
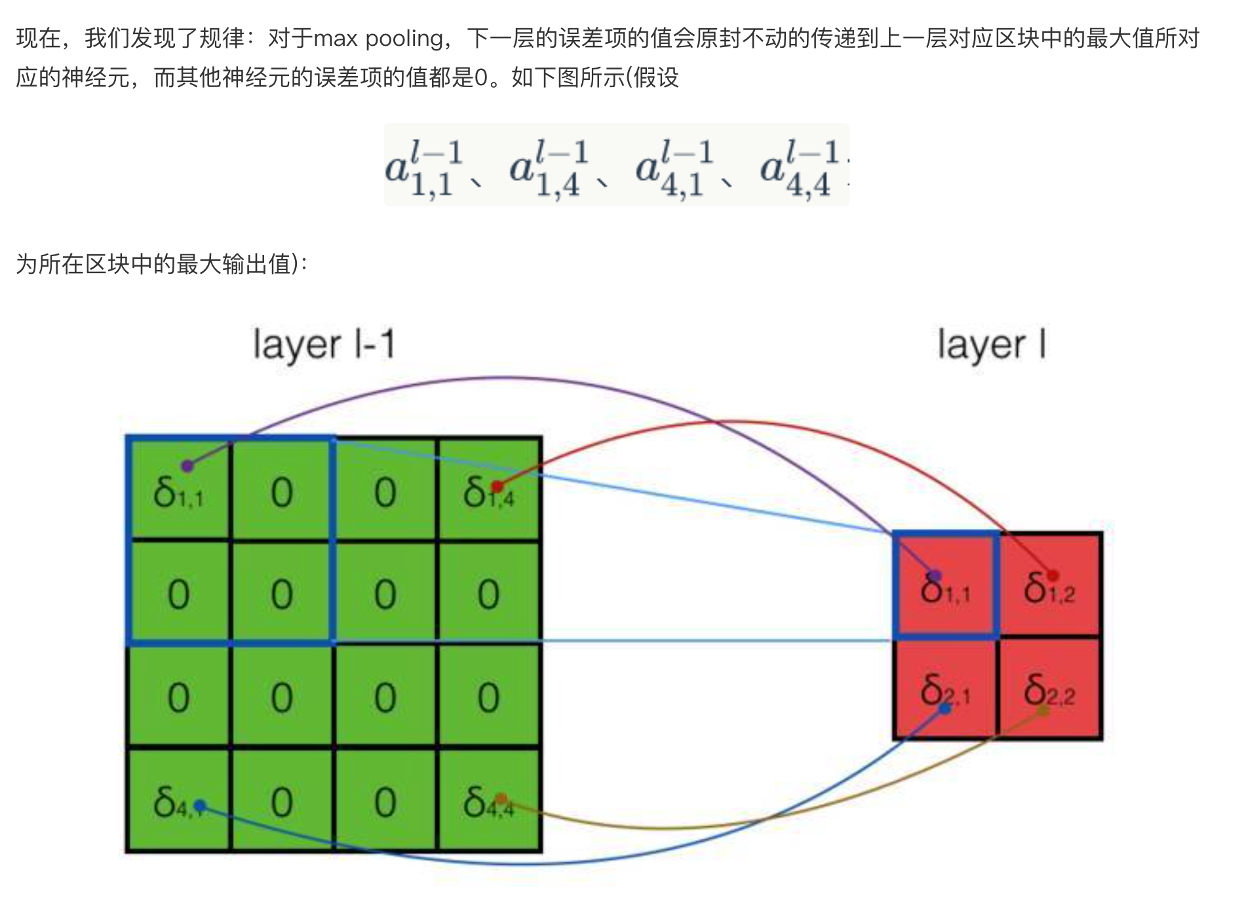
任务:实现反向计算误差项
- 请实现反向计算误差项?
答:待实现的代码为:MaxPoolingLayer,实现后的代码为:MaxPoolingLayer.res_answer
总结
- 请总结本节课的内容?
- 请回答开始的问题?
参考资料
扩展阅读
无



 浙公网安备 33010602011771号
浙公网安备 33010602011771号