深度学习基础课：卷积层的后向传播推导
大家好~本课程为“深度学习基础班”的线上课程，带领同学从0开始学习全连接和卷积神经网络，进行数学推导，并且实现可以运行的Demo程序
线上课程资料：
加QQ群，获得ppt等资料，与群主交流讨论：106047770
本系列文章为线上课程的复盘，每上完一节课就会同步发布对应的文章
本课程系列文章可进入索引查看：
目录
回顾相关课程内容
- 卷积神经网络的局部连接和权重共享是指什么？
- 卷积层的前向传播是如何计算的？
- 全连接层的后向传播算法是什么？
答：先计算输出层的误差项，然后反向依次计算每层的误差项直到与输入层相连的层，最后根据每层的误差项和输入得到每层的梯度 - 误差项的计算公式是什么？
答：\(\delta_k=\frac{dE}{dnet_k}\) - 全连接层的后向传播是如何推导？
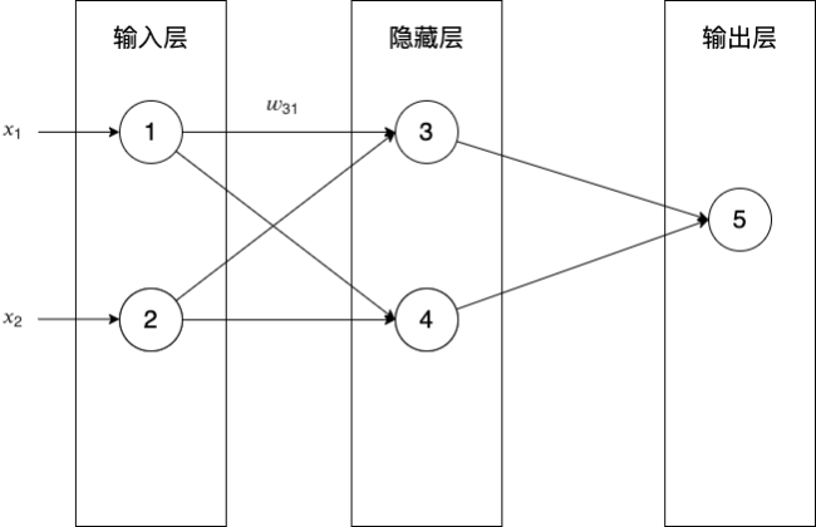
为什么要学习本课
- 如何推导卷积层的后向传播？
主问题：如何推导卷积层的后向传播？
- 卷积层的后向传播算法有哪些步骤？
答：
1.已知下一层计算的误差项，反向依次计算这一层的误差项
2.计算这一层中每个权重值的梯度 - 与全连接层中隐藏层的后向传播算法的步骤一样吗？有什么区别？
答：步骤跟隐藏层是一样的，但是每个步骤的计算方法都不一样，这是因为：
“局部连接”使得第一步误差项的计算方法不一样；
“权值共享”则使得第二步变为计算Filter中的每个权重值的梯度； - 下面分别讨论这两个步骤的实现
主问题：如何反向计算误差项？
- 我们先来考虑步长为1、输入的深度为1、filter个数为1的最简单的情况。
- 假设输入的大小为33，filter大小为22，按步长为1卷积，我们将得到2*2的feature map。如下图所示：
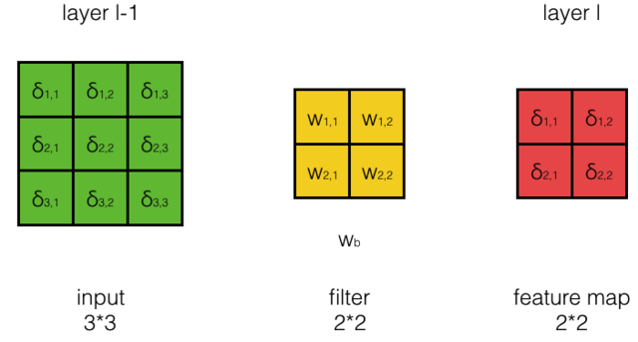
- 其中layer l-1为当前层（卷积层），layer l为下一层
- 在这里，我们假设第l层中的每个误差项都已经算好，我们要做的是计算第l-1层每个神经元的误差项
- 它的计算公式是什么：
\[\delta_{i,j}^{l-1}=? \\
\delta_{i,j}^{l-1}表示第l-1层第i行第j列的误差项
\]
答：
\[\begin{aligned}
\delta_{i,j}^{l-1} &= \frac{dE}{dnet_{i,j}^{l-1}} \\
&= \frac{dE}{da_{i,j}^{l-1}}\frac{da_{i,j}^{l-1}}{dnet_{i,j}^{l-1}}\\
\end{aligned}
\]
\[a_{i,j}^{l-1}表示第l-1层第i行第j列神经元的输出 \\
net_{i,j}^{l-1}表示第l-1层第i行第j列神经元的加权输入 \\
\]
-
如何求\(\frac{dE}{da_{i,j}^{l-1}}\)？
- 我们先来看几个特例，然后从中总结出一般性的规律：
- 计算\(\frac{dE}{da_{1,1}^{l-1}}\)？
答：
\( 因为a_{1,1}^{l-1}只与net_{1,1}^l有关，且net_{1,1}^l = w_{1,1}a_{1,1}^{l-1} + w_{1,2}a_{1,2}^{l-1} + w_{2,1}a_{2,1}^{l-1} + w_{2,2}a_{2,2}^{l-1} + w_b \\ 所以\frac{dE}{da_{1,1}^{l-1}}=\frac{dE}{dnet_{1,1}^{l}}\frac{dnet_{1,1}^l}{da_{1,1}^{l-1}} = \delta_{1,1}^l w_{1,1} \) - 计算\(\frac{dE}{da_{1,2}^{l-1}}\)？
答：\( 因为a_{1,2}^{l-1}与net_{1,1}^l, net_{1,2}^l有关，且\\ net_{1,1}^l = w_{1,1}a_{1,1}^{l-1} + w_{1,2}a_{1,2}^{l-1} + w_{2,1}a_{2,1}^{l-1} + w_{2,2}a_{2,2}^{l-1} + w_b \\ net_{1,2}^l = w_{1,1}a_{1,2}^{l-1} + w_{1,2}a_{1,3}^{l-1} + w_{2,1}a_{2,2}^{l-1} + w_{2,2}a_{2,3}^{l-1} + w_b \\ 所以\frac{dE}{da_{1,2}^{l-1}}=\frac{dE}{dnet_{1,1}^{l}}\frac{dnet_{1,1}^l}{da_{1,2}^{l-1}} + \frac{dE}{dnet_{1,2}^{l}}\frac{dnet_{1,2}^l}{da_{1,2}^{l-1}} \\ = \delta_{1,1}^l w_{1,2} + \delta_{1,2}^l w_{1,1} \) - 请总结出规律？
答：\( 不难发现，计算\frac{dE}{da_{i,j}^{l-1}}，相当于把第l层误差项的周围补一圈0， 再与180度翻转后的filter进行互相关操作，就能得到想要结果，如下图所示： \)
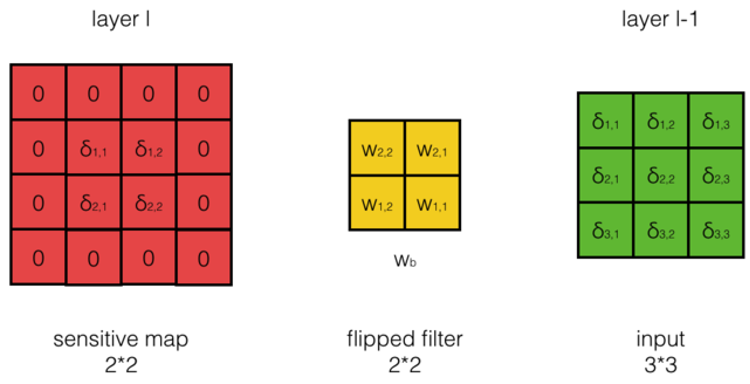
计算公式是什么？
答：
\( \frac{dE}{da^{l-1}} = cross(padding(\delta^l), rotate180(W)) \\ \)
- 计算\(\frac{dE}{da_{1,1}^{l-1}}\)？
- 我们先来看几个特例，然后从中总结出一般性的规律：
-
如何求\(\frac{da_{i,j}^{l-1}}{dnet_{i,j}^{l-1}}=?\)
答：
\[\because
a_{i,j}^{l-1} = f(net_{i,j}^{l-1}) \\
\therefore\frac{da_{i,j}^{l-1}}{dnet_{i,j}^{l-1}}= f'(net_{i,j}^{l-1})
\]
- 因此，我们得到了最终的公式：
\[\begin{aligned}
\delta^{l-1} &= \frac{dE}{dnet^{l-1}} \\
&= \frac{dE}{da^{l-1}}\frac{da^{l-1}}{dnet^{l-1}} \\
&= cross(padding(\delta^l), rotate180(W)) \circ f'(net^{l-1}) \\
\end{aligned}
\]
\[其中：\\
\delta^{l-1}, \delta^l, W, net^{l-1}都是矩阵\\
符号\circ为element \, wise \, product，即将矩阵中每个对应元素相乘
\]
- 下面我们来推导步长为S的情况
- 我们来看看步长为2与步长为1的差别：
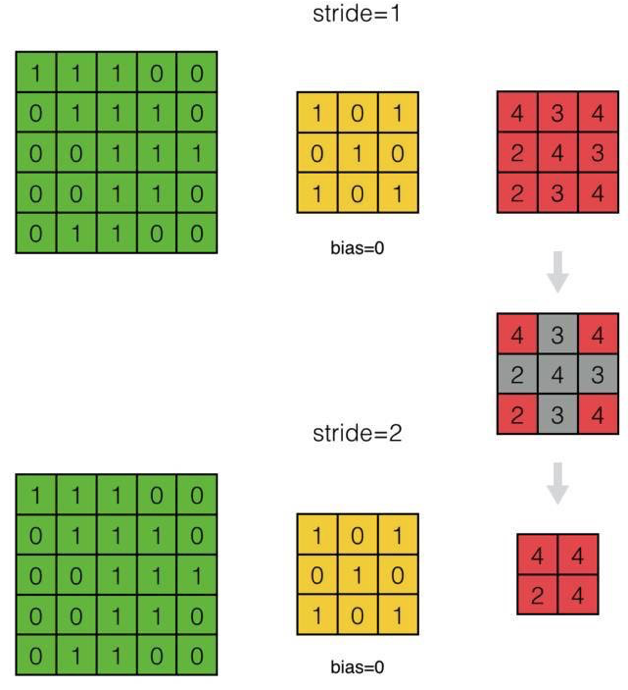
- 如何处理步长为2的情况？
- 如何将其统一为步长为1的情况？
答：我们可以看出，因为步长为2，得到的feature map跳过了步长为1时相应的部分。因此，当我们反向计算误差项时，我们可以对步长为S的\(\delta^l\)相应的位置进行补0，将其『还原』成步长为1时的\(\delta^l\)
- 如何将其统一为步长为1的情况？
- 下面我们来推导深度为D和Filter个数为N的情况
- 如果把每个深度看成一个结点，把互相关操作变成乘上权重，则深度为3、Filter个数为2的情况如下图所示：
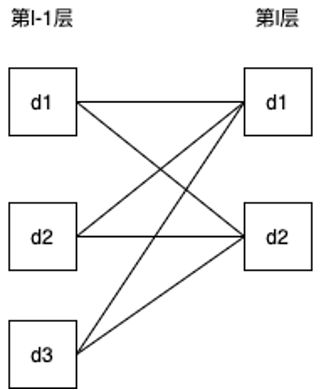
- 第l-1层的d1影响了第l层的哪几个结点？
答：影响了第l层的所有结点，包括第l层的d1,d2 - 所以第l-1层的d1的误差项应该等于什么？
答：\(= 第l层的d1的误差项与第一个Filter反向计算出的第l-1层的误差项 + 第l层的d2的误差项与第二个Filter反向计算出的第l-1层的误差项\) - 因此，可以将误差项计算公式改为什么？
答：
\[\begin{aligned}
\delta_d^{l-1}
&= \sum_{n=0}^{N-1} cross(padding(\delta_n^l), rotate180(W_{d, n})) \circ f'(net^{l-1}) \\
\end{aligned}
\]
\[其中：\\
d为深度序号，即第d层\\
n为Filter的序号，即第n个Filter\\
\]
结学
- 如何反向计算误差项？
任务：实现反向计算误差项
- 请实现反向计算误差项？
答：待实现的函数为ConvLayer->bpDeltaMap函数，实现后的函数为：ConvLayer->bpDeltaMap函数
主问题：如何计算Filter每个权重值的梯度？
- 我们要在得到本层的误差项的情况下，计算本层的Filter的权重的梯度
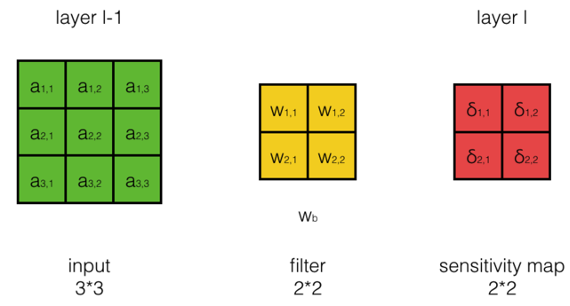
\[如上图所示，a_{i,j}^{l-1} 是第l-1层的输出，W_{i,j}是第l层filter的权重，\delta_{i,j}^{l} 是第l层的误差项。我们的任务是计算W_{i,j}的梯度，即\frac{dE}{dw_{i,j}}\\
为了计算偏导数，我们需要考察权重W_{i,j}对E的影响：\\
权重项W_{i,j}通过影响net_{i,j}^l的值，进而影响E \\
我们仍然通过几个具体的例子来看权重项W_{i,j}对net_{i,j}^l的影响，然后再从中总结出规律。
\]
- 计算\(\frac{dE}{dw_{1,1}}\)？
- \(w_{1,1}对哪几个net_{i,j}^l有影响？\)
答：
\[net_{1,1}^l = w_{1,1}a_{1,1}^{l-1} + w_{1,2}a_{1,2}^{l-1} + w_{2,1}a_{2,1}^{l-1} + w_{2,2}a_{2,2}^{l-1} + w_b \\
net_{1,2}^l = w_{1,1}a_{1,2}^{l-1} + w_{1,2}a_{1,3}^{l-1} + w_{2,1}a_{2,2}^{l-1} + w_{2,2}a_{2,3}^{l-1} + w_b \\
net_{2,1}^l = w_{1,1}a_{2,1}^{l-1} + w_{1,2}a_{2,2}^{l-1} + w_{2,1}a_{3,1}^{l-1} + w_{2,2}a_{3,2}^{l-1} + w_b \\
net_{2,2}^l = w_{1,1}a_{2,2}^{l-1} + w_{1,2}a_{2,3}^{l-1} + w_{2,1}a_{3,2}^{l-1} + w_{2,2}a_{3,3}^{l-1} + w_b \\
\]
\[从上面的公式看出，由于权值共享，权值W1,1对所有的net_{i,j}^l有影响\\
因为E是所有所有的net_{i,j}^l的函数，而所有的net_{i,j}^l又都是w_{1,1}的函数\\
所以根据全导数公式，计算\frac{dE}{dw_{1,1}}是要把每个偏导数都加起来：\\
\]
\[\begin{aligned}
\frac{dE}{dw_{1,1}} &= \frac{dE}{dnet_{1,1}^l}\frac{{dnet_{1,1}^l}}{dw_{1,1}} + \frac{dE}{dnet_{1,2}^l}\frac{{dnet_{1,2}^l}}{dw_{1,1}} + \frac{dE}{dnet_{2,1}^l}\frac{{dnet_{2,1}^l}}{dw_{1,1}} + \frac{dE}{dnet_{2,2}^l}\frac{{dnet_{2,2}^l}}{dw_{1,1}} \\
&= \delta_{1,1}^l a_{1,1}^{l-1} + \delta_{1,2}^l a_{1,2}^{l-1} + \delta_{2,1}^l a_{2,1}^{l-1} + \delta_{2,2}^l a_{2,2}^{l-1}
\end{aligned}
\]
- 计算\(\frac{dE}{dw_{1,2}}\)
答：
\[\begin{aligned}
\frac{dE}{dw_{1,2}} &= \delta_{1,1}^l a_{1,2}^{l-1} + \delta_{1,2}^l a_{1,3}^{l-1} + \delta_{2,1}^l a_{2,3}^{l-1} + \delta_{2,2}^l a_{2,3}^{l-1}
\end{aligned}
\]
- 实际上，每个权重项导数的计算都是类似的，我们不一一举例了
- 现在，是我们再次发挥想象力的时候，我们发现计算\(\frac{dE}{dw_{i,j}}\)的规律是什么？
答：
\[\frac{dE}{dw_{i,j}} = \sum_m \sum_n \delta_{m,n}^l a_{i+m, j+n}^{l-1}
\]
也就是用误差项作为卷积核，在input上进行互相关操作，如下图所示：
- 如何求偏置项的梯度\(\frac{dE}{dw_b}\)？
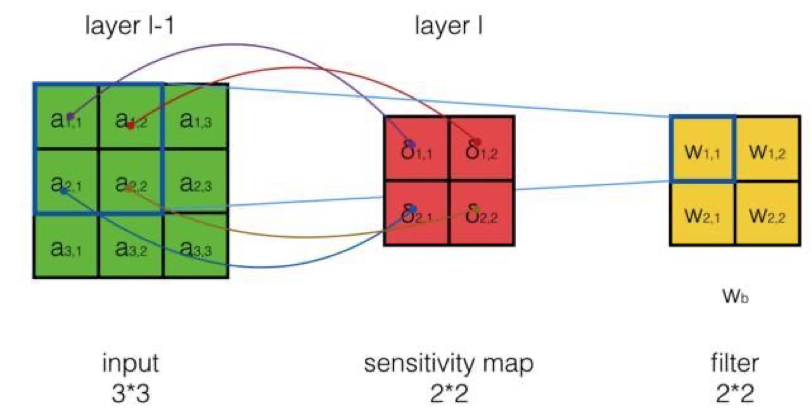
答：
\[\begin{aligned}
\frac{dE}{dw_b} &= \frac{dE}{dnet_{1,1}^l}\frac{dnet_{1,1}^l}{w_b} + \frac{dE}{dnet_{1,2}^l}\frac{dnet_{1,2}^l}{w_b} + \frac{dE}{dnet_{2,1}^l}\frac{dnet_{2,1}^l}{w_b} + \frac{dE}{dnet_{2,2}^l}\frac{dnet_{2,2}^l}{w_b} \\
&= \delta_{1,1}^l + \delta_{1,2}^l + \delta_{2,1}^l + \delta_{2,2}^l \\
&= \sum_i \sum_j \delta_{i,j}^l
\end{aligned}
\]
\[
也就是偏置项的梯度就是所有误差项之和
\]
- 如何处理步长为2的情况？
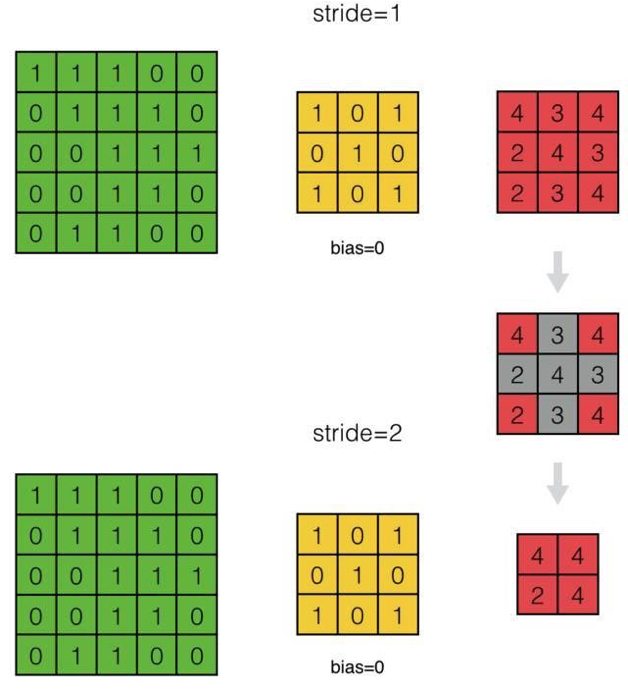
答：对于步长为S的卷积层，处理方法与传递误差项时一样： 通过对\(\delta^l\)补0，将其『还原』成步长为1的情况
- 对于Filter个数为N和每个Filter的深度为D的情况，因为每个都对应输出图像的对应深度的Feature map和输入图像的对应深度的Feature map，每一个二维Filter只涉及到一次二维卷积运算
- 所以只需分别计算N×D次每个二维Filter的导数，再将其组合成4维张量，即可求得整个Filter的导数
结学
- 如何计算Filter每个权重值的梯度？
任务：实现计算Filter每个权重值的梯度
- 请实现计算Filter每个权重值的梯度？
答：待实现的代码为：ConvLayer_compute_gradient，实现后的代码为：ConvLayer_compute_gradient_answer, Filter_answer
总结
- 请总结本节课的内容？
- 请回答开始的问题？
参考资料
扩展阅读
- 卷积神经网络(CNN)反向传播算法推导
有详细的数学推导(比如本课程中通过找规律得到的公式，在该文中有数学推导)
感谢您的阅读~
扫码加入我的QQ群：
扫码加入免费知识星球-YYC的Web3D旅程：
