真实感渲染:变换(二维与三维)
大家好~本课程为“真实感渲染”的线上课程,从0开始,介绍相关的图形学算法和数学基础,给出详细的数学推导、伪代码和实现代码,最终带领大家开发出基于物理的渲染器
线上课程资料:
加QQ群,获得ppt等资料,与群主交流讨论:106047770
本系列文章为线上课程的复盘,每上完一节课就会同步发布对应的文章
本课程系列文章可进入索引查看:
真实感渲染系列文章索引
回顾相关课程
- 什么是矩阵?
为什么要学习本课
-
3D中物体有哪些变换?
答:平移、旋转、缩放 -
演示相关的变换
-
3D到2D的投影需要进行变换
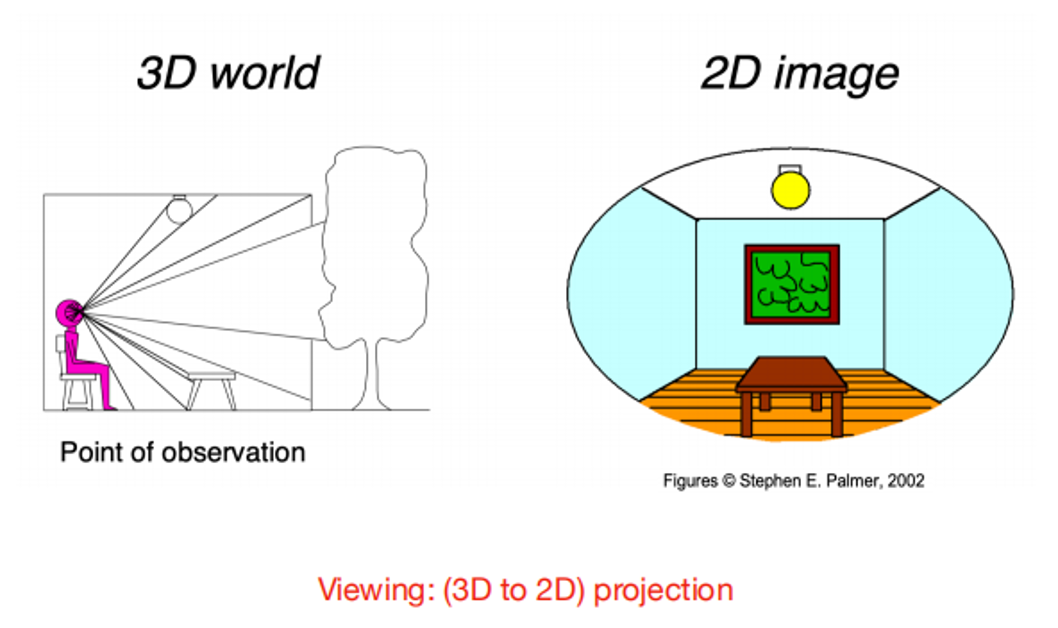
主问题:什么是2D变换
-
如何进行缩放?
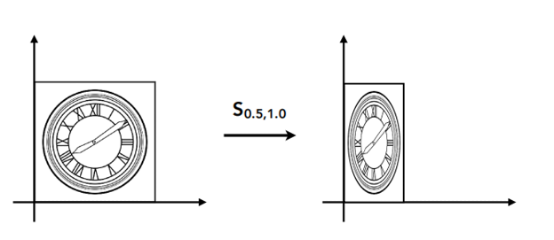
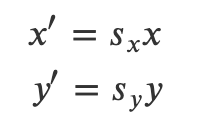
-
缩放矩阵是多少?
答: \( \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} s_x & 0 \\ 0 & s_y \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \) -
如何进行反射?
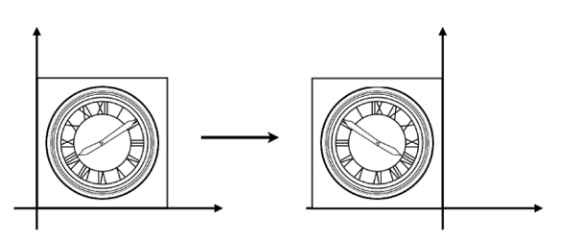
- 反射矩阵是多少?
答: \( \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \)
- 反射矩阵是多少?
-
-
如何进行旋转?
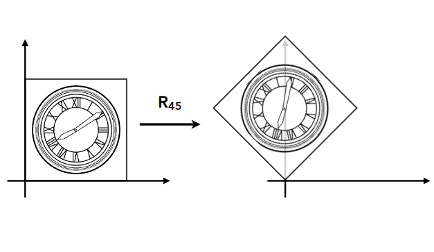
默认为绕着原点(0, 0)逆时针旋转- 旋转矩阵是多少?
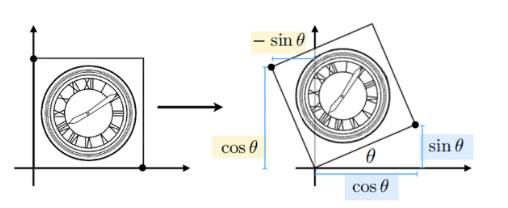
\( R_\theta = \begin{bmatrix} ? & ? \\ ? & ? \end{bmatrix} \)
答:\( R_\theta = \begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix} \)
- 旋转矩阵是多少?
推导过程如下图所示:
通过变换(1,0)点,可以得到矩阵的A、C值:
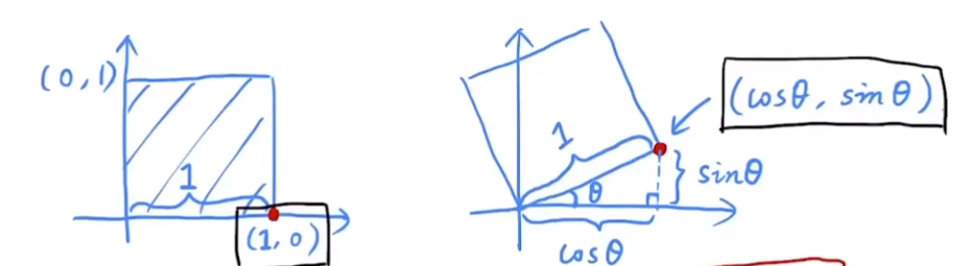
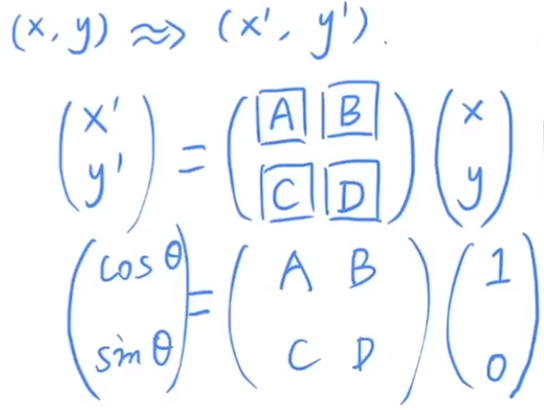
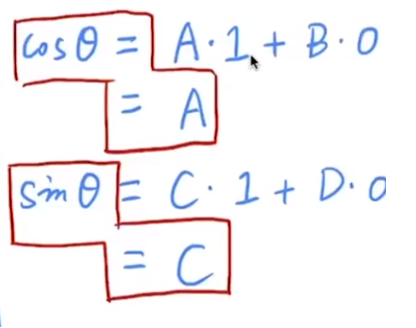
同理,通过变换(0,1)点,可以得到矩阵的B、D值
-
什么是线性变换?
答: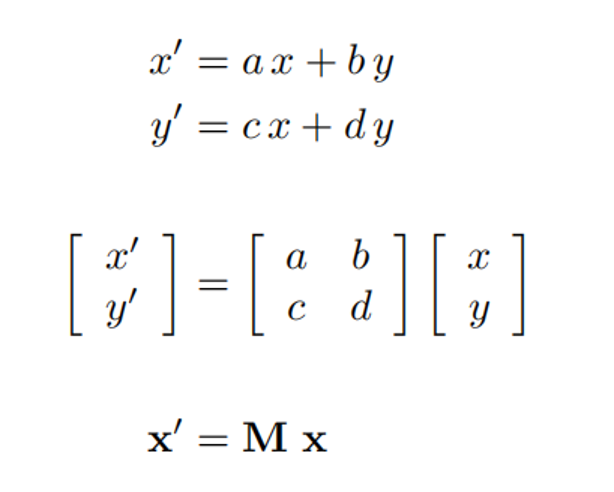
-
缩放和旋转是否属于线性变换?
答:是 -
如何进行平移?
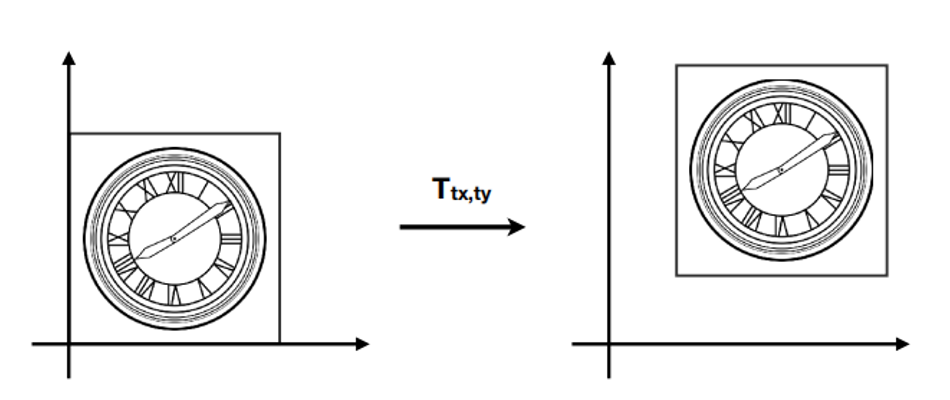
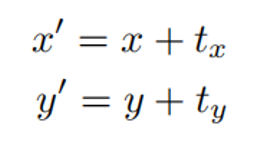
- 它的表达式是什么?
答:
- 它的表达式是什么?
- 如何进行平移?
- 能够得到2D的平移矩阵吗?
答:不能 - 平移属于线性变换吗?
答:不属于
- 能够得到2D的平移矩阵吗?
主问题:什么是齐次坐标
为什么要引入“齐次坐标”
-
如何才能统一缩放、旋转、平移为都使用一个矩阵来变换?
答:引入齐次坐标 -
什么是齐次坐标?
答: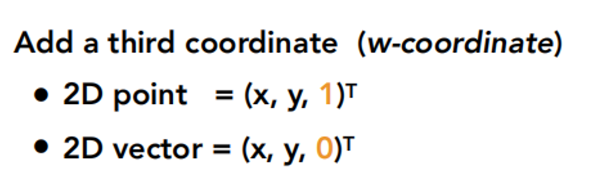
-
向量+向量=?
答:向量 -
点-点=?
答:向量 -
点+向量=?
答:点 -
\( \begin{bmatrix} x \\ y \\ w \end{bmatrix} = ? \\ 其中:w \neq 0 \)
答:
\( \begin{bmatrix} x \\ y \\ w \end{bmatrix} = 2D 点: \begin{bmatrix} \frac{x}{w} \\ \frac{y}{w} \\ 1 \end{bmatrix} \) -
点+点=?
答:因为相加的结果经过上面的变换后,可变换为点,所以相加的结果为点 -
用加了齐次坐标的矩阵来表达平移的表达式是什么?
答:
主问题:更多的2D变换有哪些
-
什么是仿射变换?
答:
-
用齐次坐标后如何修改?
答: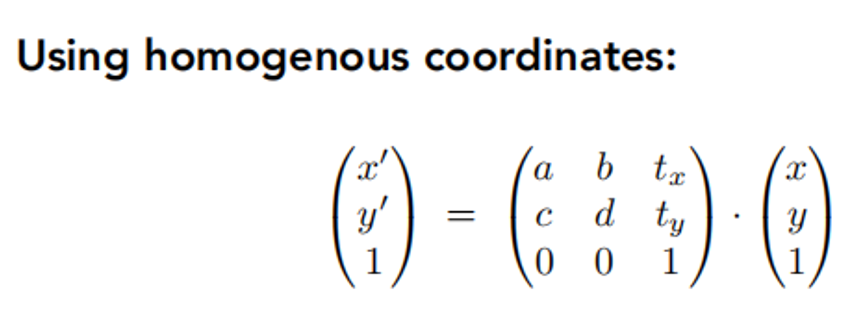
-
用齐次坐标后,缩放、旋转、平移的矩阵是什么?
答: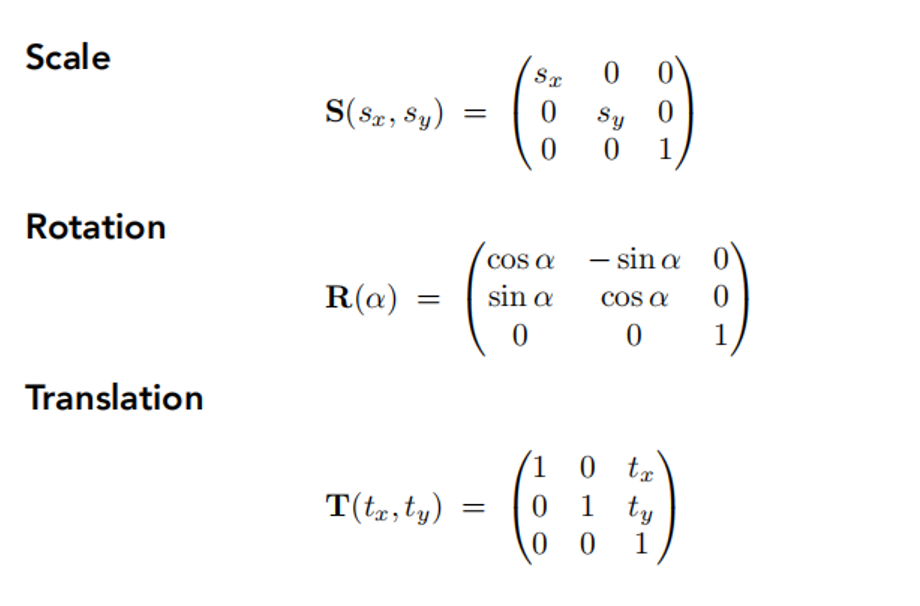
-
什么是逆变换?
答: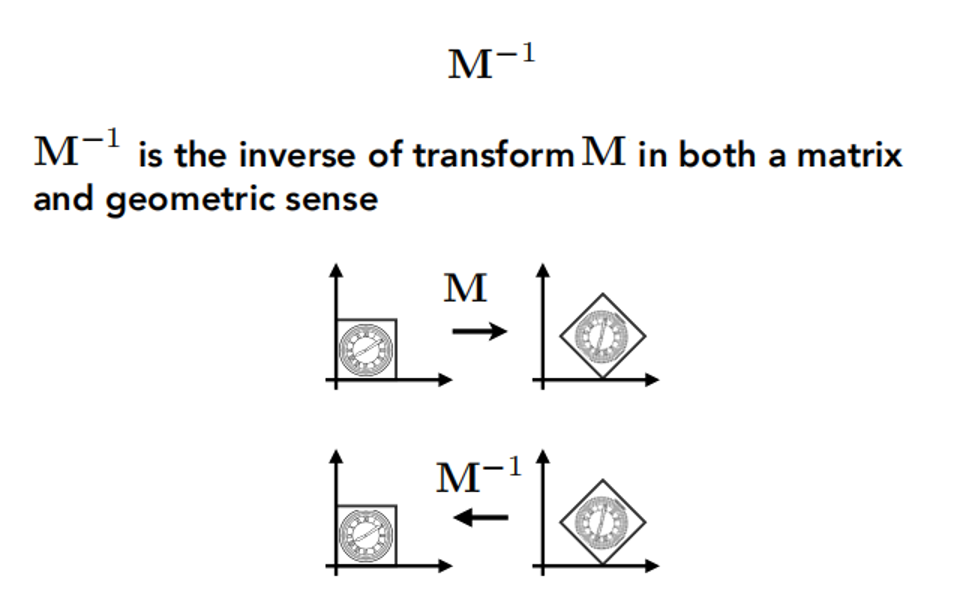
-
如何进行组合变换?
- 如何进行下图的变换?
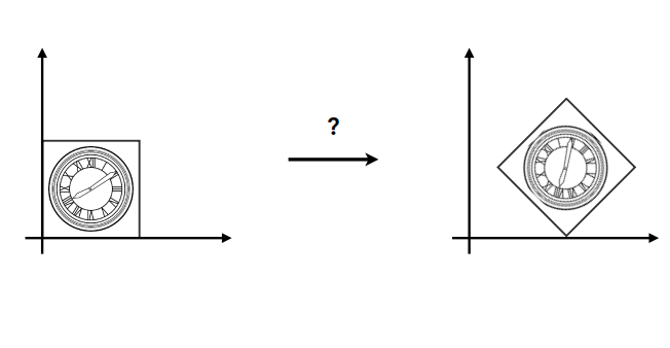
答:有两种方式:先位移再旋转和先旋转再位移
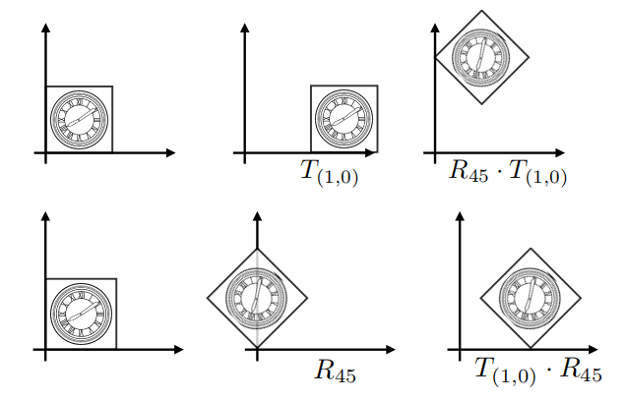
- 如何进行下图的变换?
变换的顺序对结果有影响!

这里应该使用先旋转再位移,表达式为:
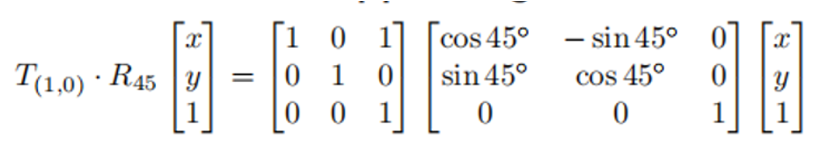
- 如何进行组合变换?
-
如何提高性能?
答:
-
如何绕一个点旋转?
答: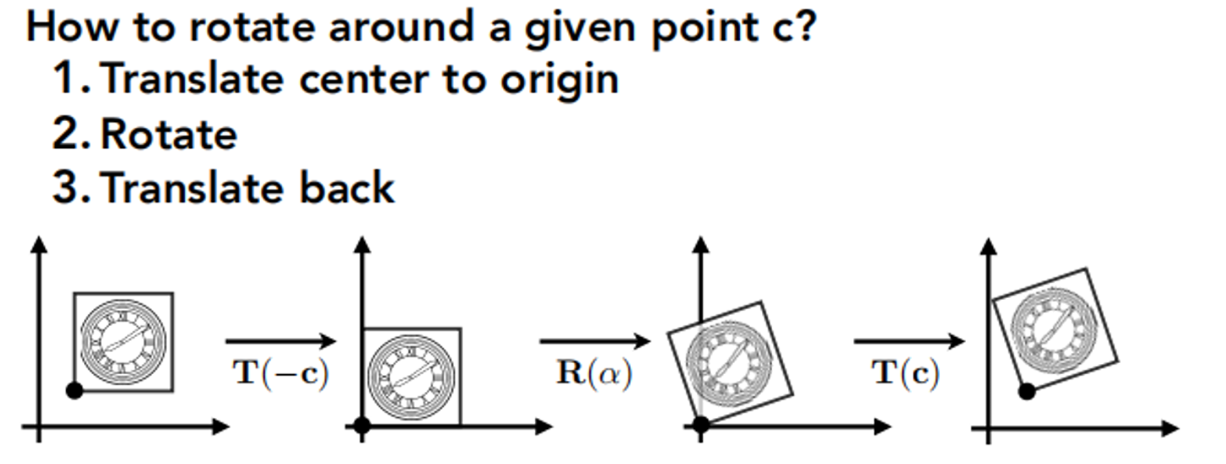
-
表达式是什么?
答: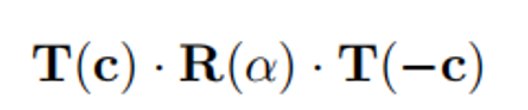
-
主问题:什么是3D变换
-
什么是3D的齐次坐标?
答: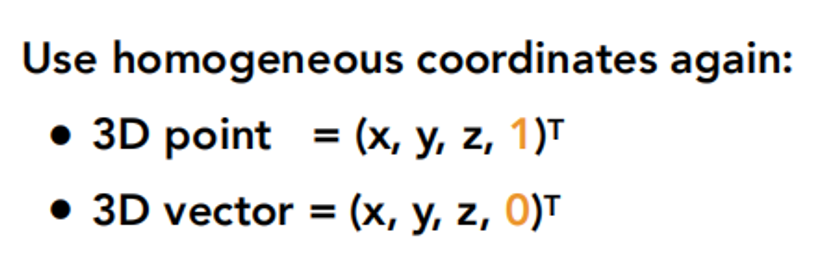
-
\( \begin{bmatrix} x \\ y \\ z\\ w \end{bmatrix} = ? \\ 其中:w \neq 0 \)
答:
\( \begin{bmatrix} x \\ y \\ z\\ w \end{bmatrix} = 3D 点: \begin{bmatrix} \frac{x}{w} \\ \frac{y}{w} \\ \frac{z}{w} \\ 1 \end{bmatrix} \) -
什么是3D的仿射变换?
答:
- 用齐次坐标后如何修改?
答:
总结
- 请总结本节课的内容?
- 请回答开始的问题?




 浙公网安备 33010602011771号
浙公网安备 33010602011771号