深度学习基础课：卷积神经网络与卷积层的前向传播推导

大家好~本课程为“深度学习基础班”的线上课程，带领同学从0开始学习全连接和卷积神经网络，进行数学推导，并且实现可以运行的Demo程序

线上课程资料：

本节课录像回放1

本节课录像回放2

加QQ群，获得ppt等资料，与群主交流讨论：106047770

本系列文章为线上课程的复盘，每上完一节课就会同步发布对应的文章

本课程系列文章可进入索引查看：
深度学习基础课系列文章索引

目录

• 回顾相关课程内容
• 为什么要学习本课
• 主问题：卷积神经网络是什么？
  • 为什么引入卷积神经网络？
  • 主问题：卷积神经网络是什么？
• 主问题：Relu激活函数是什么？
• 任务：实现Relu激活函数
• 主问题：如何推导卷积层的前向传播？
  • 结学
• 任务：实现卷积层的前向传播
• 总结
• 参考资料

回顾相关课程内容

• 如何使用全连接神经网络识别手写数字？
  

  • 网络结构是什么？

为什么要学习本课

• 全连接神经网络用于图像识别任务有什么问题？
  

• 卷积神经网络是怎样解决这些问题的？

• Relu激活函数是什么？

• 如何推导卷积层的前向传播？

主问题：卷积神经网络是什么？

为什么引入卷积神经网络？

• 全连接神经网络用于图像识别任务有什么问题？

答：

1、参数数量太多

考虑一个输入1000*1000像素的图片，输入层有1000*1000=100万节点。假设第一个隐藏层有100个节点，那么仅这一层就有(1000*1000+1)*100=1亿参数！
而且图像只扩大一点，参数数量就会多很多，因此它的扩展性很差。

2、没有利用像素之间的位置信息

对于图像识别任务来说，每个像素和其周围像素的联系是比较紧密的，和离得很远的像素的联系可能就很小了。如果一个神经元和上一层所有神经元相连，那么就相当于对于一个像素来说，把图像的所有像素都等同看待，这不符合前面的假设。当我们完成每个连接权重的学习之后，最终可能会发现，有大量的权重，它们的值都是很小的(也就是这些连接其实无关紧要)。努力学习大量并不重要的权重，这样的学习必将是非常低效的。

3、网络层数限制

我们知道网络层数越多其表达能力越强，但是通过梯度下降方法训练深度全连接神经网络很困难，因为全连接神经网络的梯度很难传递超过3层。因此，我们不可能得到一个很深的全连接神经网络，也就限制了它的能力。

• 卷积神经网络是怎样解决这些问题的？

答：

1、局部连接

这个是最容易想到的，每个神经元不再和上一层的所有神经元相连，而只和一小部分神经元相连。这样就减少了很多参数。

2、权值共享

一组连接可以共享同一个权重，而不是每个连接有一个不同的权重，这样又减少了很多参数。

3、下采样

可以使用池化（Pooling）来减少每层的样本数，进一步减少参数数量，同时还可以提升模型的鲁棒性。

主问题：卷积神经网络是什么？

图1

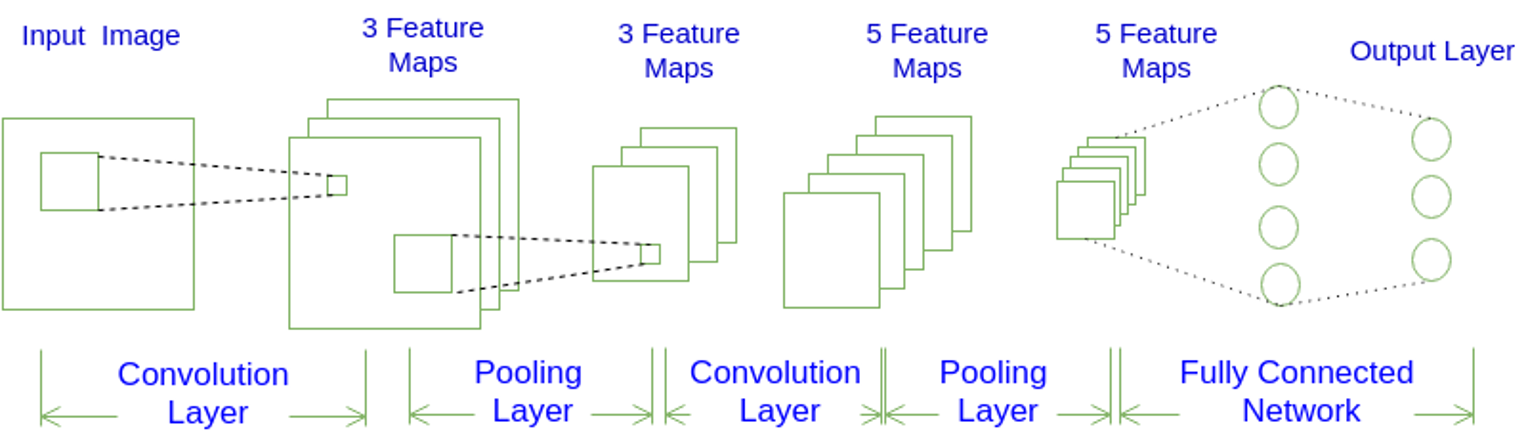
• 如图1所示，一个卷积神经网络由若干卷积层、池化层、全连接层组成

• 常用架构模式为：INPUT -> [[CONV]N -> POOL?]M -> [FC]*K

• 也就是N个卷积层叠加，然后(可选)叠加一个池化层，重复这个结构M次，最后叠加K个全连接层

• 图1的N、M、K为多少？
  答：N=1, M=2, K=2

• 与全连接神经网络相比，卷积神经网络有什么不同？
  全连接神经网络：
  

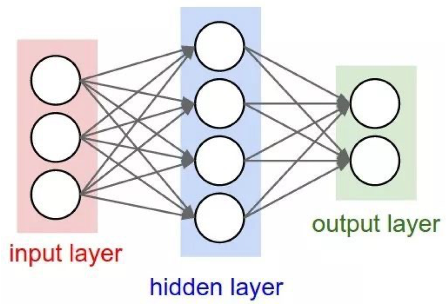
• 什么是Filter？Filter与卷积层是什么关系？
  答：Filter是卷积核，是一组参数，用来提取特征到Feature Map中。Filter的宽度和高度一般是相等的。
  卷积层包含多个Filter

• Filter的数量与Feature Map的数量有什么关系？
  答：卷积层包含的Filter的数量和卷积层输出的Feature Map的数量是相等的，一一对应的

• 如何理解Feature Map？
  答：Feature Map保存了Filter提取的特征。如一个Filter为提取图像边缘的卷积核，那么对应的Feature Map就保存了图像边缘的特征

• 池化层在做什么？
  答：下采样，即将Feature Map缩小

• 全连接层跟Feature Maps如何连接？
  答：全连接层的神经元跟所有的Feature Map的像素一一对应，如Feature Maps有5个，每个有30个像素数据，那么与其连接的全连接层就有150个神经元

• 请整体描述图1卷积神经网络的前向传播过程？

主问题：Relu激活函数是什么？

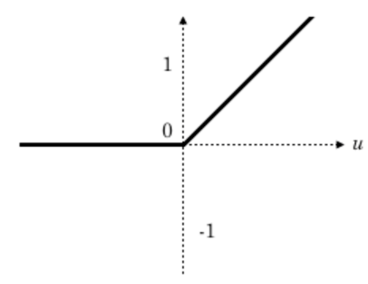
• Relu的定义是什么？
  答：$f(x)=max(0,x)$
  

• 与Sigmoid相比，Relu有什么优势？
  答：

1、速度快

2、减轻梯度消失问题

全连接隐藏层的误差项公式如下，它会乘以激活函数的导数：

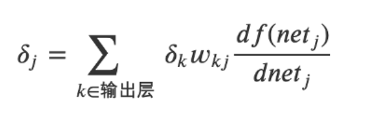
而Sigmoid激活函数的导数的图形如下所示：

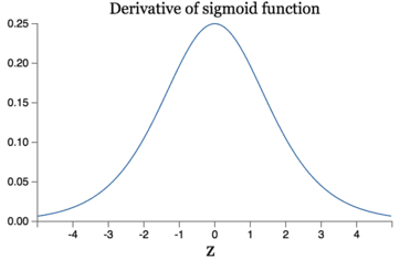
可知它的导数的最大值为$\frac{1}{4}$，所以第一个全连接隐藏层的误差项会至少衰减为原来的$\frac{1}{4}$，上一个全连接隐藏层的误差项则至少衰减为原来的$\frac{1}{16}$，以此类推，导致层数越多越容易出现梯度消失的问题

而Relu的导数为1，所以不会导致误差项的衰减

3、稀疏性

通过对大脑的研究发现，大脑在工作的时候只有大约5%的神经元是激活的。有论文声称人工神经网络在15%-30%的激活率时是比较理想的。因为relu函数在输入小于0时是完全不激活的，因此可以获得一个更低的激活率。

任务：实现Relu激活函数

• 请实现Relu激活函数
  答：待实现的代码为：ReluActivator，实现后的代码为：ReluActivator_answer

主问题：如何推导卷积层的前向传播？

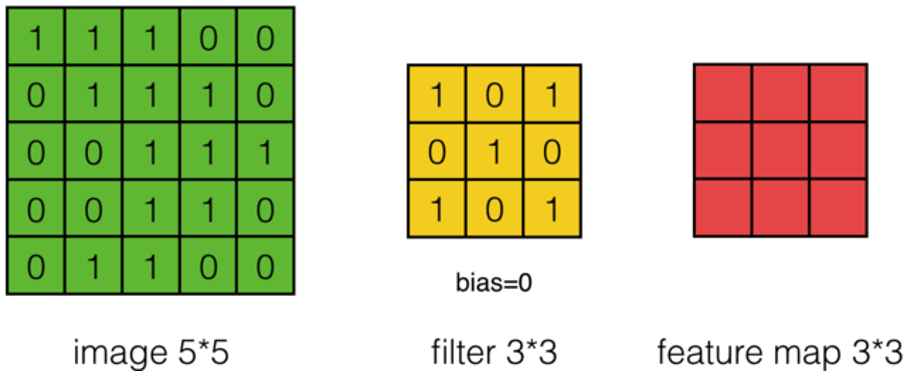
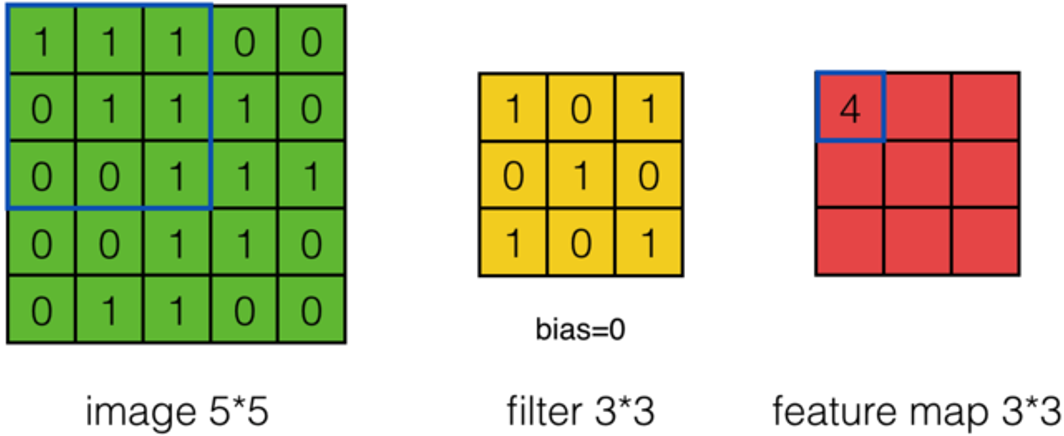
• 假设有一个55的图像，使用一个33的filter进行卷积，想得到一个3*3的Feature Map，如下图所示：
  

• 使用下列公式计算卷积：

$$a_{i,j} = f(\sum_{m=0}^2 \sum_{n=0}^2 w_{m,n}x_{i+m,j+n} + w_b)$$

$$对图像的每个像素进行编号，用x_{i,j}表示图像的第i行第j列元素；\\ 对filter的每个权重进行编号，用w_{m,n}来表示第m行第n列权重，用w_b表示filter的偏置项； \\ 对Feature Map的每个元素进行编号，用a_{i,j}表示Feature Map的第i行第j列元素； \\ 用f表示激活函数$$

• $a_{0,0}=?$
  答：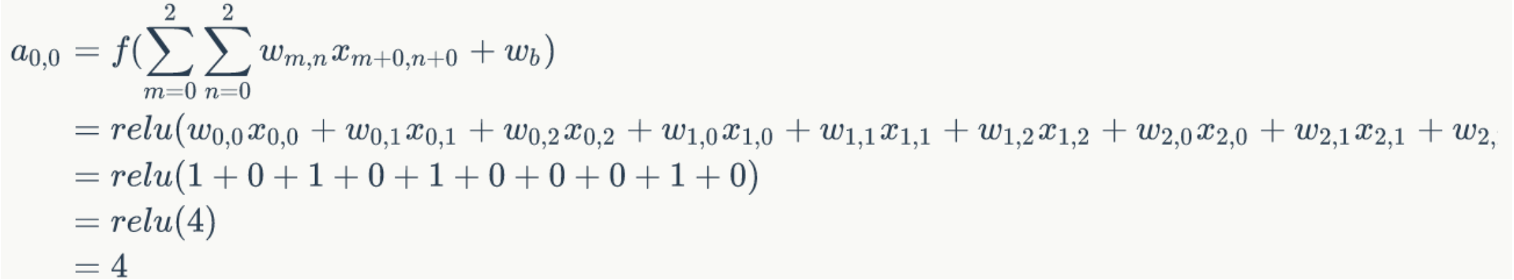
  

• $a_{0,1}=?$
  答：
  

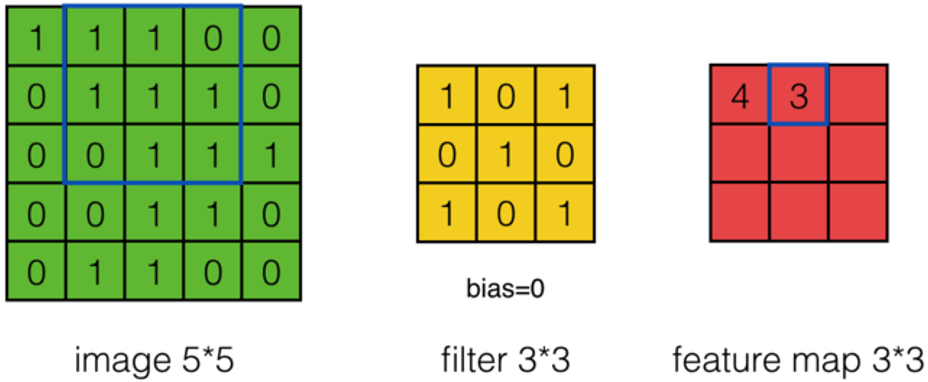
• 可以依次计算出Feature Map中所有元素的值。下面的动画显示了整个Feature Map的计算过程：
  

• 上面的计算过程中，步幅(stride)为1。步幅可以设为大于1的数。例如，当步幅为2时，Feature Map计算如下：
  
  
  
  

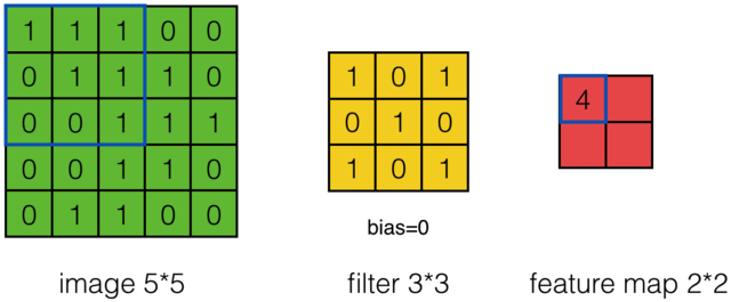
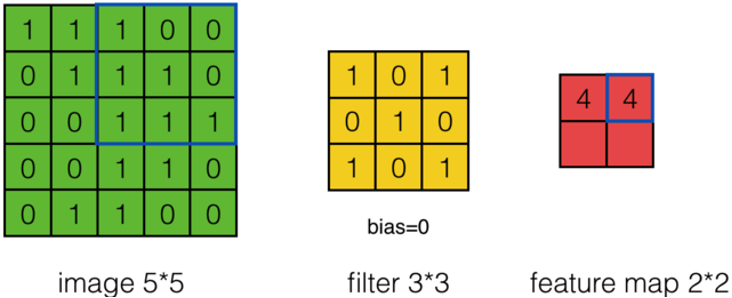
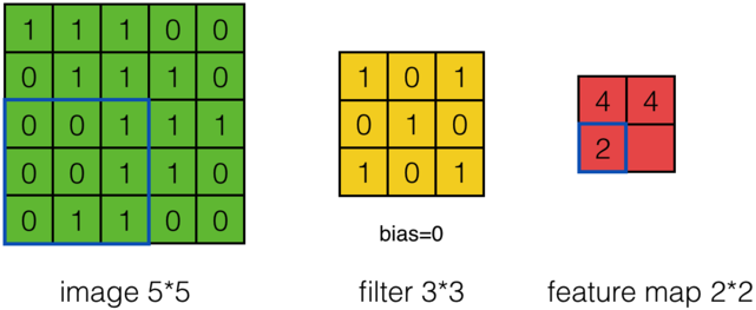
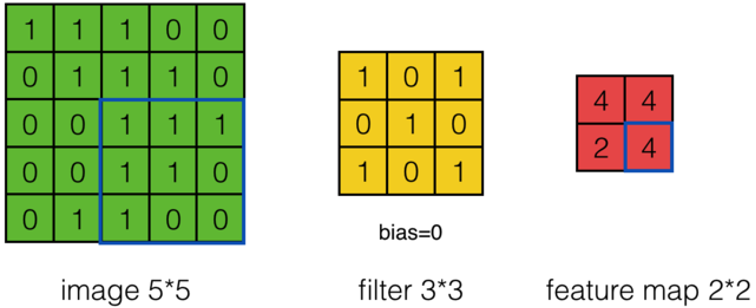
• 我们注意到，当步幅设置为2的时候，Feature Map就由$3*3$变成$2*2$了。这说明图像大小、Filter的大小、步幅、卷积后的Feature Map大小是有关系的

• 它们满足什么关系？

$$W_2 = ? \\ H_2 = ? \\ 其中，W_2是卷积后Feature Map的宽度，H_2是卷积后Feature Map的高度； \\ W_1是卷积前图像的宽度，H_1是卷积前图像的高度；\\ F是Filter的宽度（等于高度），S是步幅$$

答：

$$W_2 = \frac{W_1 - F}{S} + 1\\ H_2 = \frac{H_1 - F}{S} + 1 \\ 其中，W_2是卷积后Feature Map的宽度，H_2是卷积后Feature Map的高度； \\ W_1是卷积前图像的宽度，H_1是卷积前图像的高度；\\ F是Filter的宽度（等于高度），S是步幅$$

• 什么是Zero Padding？
  答：Zero Padding是指在原始图像周围补几圈0
• 为什么引入Zero Padding？
  答：Zero padding对于图像边缘部分的特征提取是很有帮助的
• 引入Zero Padding后，卷积后的Feature Map大小的公式应该修改为什么？
  答：

$$W_2 = \frac{W_1 - F + 2P}{S} + 1\\ H_2 = \frac{H_1 - F+ 2P}{S} + 1 \\ 其中，W_2是卷积后Feature Map的宽度，H_2是卷积后Feature Map的高度； \\ W_1是卷积前图像的宽度，H_1是卷积前图像的高度；\\ F是Filter的宽度（等于高度），S是步幅；\\ P是Zero Padding数量，如果P的值是1，那么就补1圈0$$

• 前面我们已经讲了深度为1的卷积层的计算方法，如果深度大于1怎么计算呢（步幅为1）？
  答：

$$a_{i,j} = f(\sum_{d=0}^{D-1} \sum_{m=0}^{F-1} \sum_{n=0}^{F-1} w_{d,m,n}x_{d,i+m,j+n} + w_b)$$

$$用x_{d,i,j}表示图像的第d层第i行第j列元素；\\ 用w_{d,m,n}来表示filter的第d层第m行第n列权重； \\ 其它的符号含义和之前是相同的 \\ $$

• 每个卷积层可以有多个filter。每个filter和原始图像进行卷积后，都可以得到一个Feature Map。因此，卷积后Feature Map的深度(个数)和卷积层的filter个数是相同的
• 它的计算公式是什么（步幅为1）？
  答：

$$a_{q,i,j} = f(\sum_{d=0}^{D-1} \sum_{m=0}^{F-1} \sum_{n=0}^{F-1} w_{q,d,m,n}x_{d,i+m,j+n} + w_b)$$

$$用a_{q,i,j}表示第q个Feature Map的第i行第j列元素；\\ 用w_{q,d,m,n}来表示第q个filter的第d层第m行第n列权重； \\ 其它的符号含义和之前是相同的 \\ $$

• 下面的动画显示了包含两个filter的卷积层的计算
  $7*7*3$输入->经过两个$3*3*3$filter (步幅为2)->得到了$3*3*2$的输出
  另外我们也会看到下图的Zero padding是1，也就是在输入元素的周围补了一圈0
  
  • 如何计算$a_{0,0,0}$？
  • 如何计算$a_{1,0,1}$？
• 我们把卷积神经网络中的『卷积』操作叫做互相关(cross-correlation)操作

结学

• 如何推导卷积层的前向传播？

任务：实现卷积层的前向传播

• 请实现卷积层的前向传播？
  答：待实现的代码为：ConvLayer, Filter，实现后的代码为：ConvLayer_answer, Filter_answer
  这里我们可以使用类型驱动开发的方式写代码，实现顺序为自顶向下、广度优先遍历。具体就是先实现forward函数的第一层抽象，并给出对应函数的空实现和类型定义，通过编译；然后安装广度优先遍历的顺序实现每个对应函数的第一层、第二层。。。。。。
• 请运行卷积层的代码，检查前向传播的输出是否正确？
  答：在Test.init函数中，构造了输入数据和Conv Layer；在Test.test函数中，进行了前向传播并打印了结果。结果为两个Feature Map，它的数据如下所示：

["f:",[
    [3,3,[6,7,5,3,-1,-1,2,-1,4]],
    [3,3,[2,-5,-8,1,-4,-4,0,-5,-5]]
    ]]

我们可以手动计算下$a_{0,0,0}$（注意：因为zeroPadding=1，所以要对inputs补一圈0），结果等于6，与输出的结果相同，证明forward的实现是正确的

总结

• 请总结本节课的内容？
• 请回答开始的问题？

参考资料

• 零基础入门深度学习 | 第四章：卷积神经网络