深度学习基础课：使用交叉熵损失函数和Softmax激活函数（上）

大家好~本课程为“深度学习基础班”的线上课程，带领同学从0开始学习全连接和卷积神经网络，进行数学推导，并且实现可以运行的Demo程序

线上课程资料：
本节课录像回放

加QQ群，获得ppt等资料，与群主交流讨论：106047770

本系列文章为线上课程的复盘，每上完一节课就会同步发布对应的文章

本课程系列文章可进入索引查看：
深度学习基础课系列文章索引

回顾相关课程内容
为什么要学习本课
主问题：如何加快二分类的训练速度？
- 结学
任务：判断性别Demo使用交叉熵损失函数

回顾相关课程内容

什么是训练？
训练中的收敛是指什么？

为什么要学习本课

全连接层在“判断性别Demo“的训练时，收敛得比较慢，如何加快？
全连接层在“识别手写数字“的训练时，收敛得比较慢，如何加快？

主问题：如何加快二分类的训练速度？

“判断性别Demo“属于二分类还是多分类？
答：二分类
收敛的速度决定于什么？
答：梯度越大，收敛越快
我们现在只考虑输出层
使用的是什么损失函数？
答：MSE
使用的是什么激活函数？
答：sigmoid，它的曲线如下图所示：
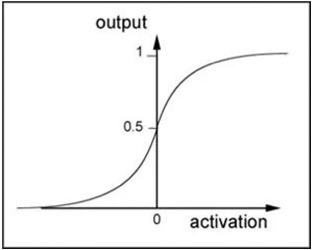
输出层的单个神经元的梯度计算公式是什么？
答：

\begin{aligned} \frac{d E}{d w_{k j}} & = δ_{k} a_{j} \\ = \frac{d E}{d y_{k}} \frac{d f (n e t_{k})}{d n e t_{k}} a_{j} \\ = - \frac{2}{n} (y_{真 实} - y_{k}) \frac{d f (n e t_{k})}{d n e t_{k}} a_{j} \end{aligned}

$\begin{aligned} \frac{dE}{dw_{kj}} &=\delta_k a_j \\ &= \frac{dE}{dy_k}\frac{df(net_k)}{dnet_k} a_j \\ &=-\frac {2}{n}(y_{真实}-y_k) \frac{df(net_k)}{dnet_k} a_j \end{aligned}$

公式中的第三项（激活函数的导数）的值跟loss的大小有什么关系？
答：loss很大或者很小时，值都很小。
这是因为 $y_{真实值}$ 只能等于0或者1，所以如果 $y_{真实值}$ 为0，那么loss很大或者很小的情况就是 $y_{输出值}$ 接近1或者0，而此时的导数是非常小的； $y_{真实值}$ 为1的情况也是一样
所以loss的大小和梯度的大小的关系是什么？
答：loss很大或者很小时，梯度都很小
所以loss的大小和收敛速度的关系是什么？
答：loss很大或者很小时，收敛速度都很慢
希望loss和梯度的关系是什么，才能尽快收敛？
答：成正比关系，即：
loss很大时，梯度很大；
loss很小时，梯度很小
误差项的大小和梯度的大小的关系是什么？
答：正比
请思考误差项的公式应该是什么样的，才能满足loss与误差项成正比，从而与梯度成正比？
答：因为 $loss=y_k - y_{真实}$ ，所以如果误差项等于loss，那么它们肯定就成正比关系。所以误差项公式为： $\delta_k=y_k - y_{真实}$
我们使用新的损失函数：交叉熵损失函数，它应该是什么，才能满足下面的公式？

\begin{aligned} E = ? 从 而 \frac{d E}{d y_{k}} \frac{d f (n e t_{k})}{d n e t_{k}} = δ_{k} = y_{k} - y_{真 实} \end{aligned}

$\begin{aligned} E = ?从而 \frac{dE}{dy_k}\frac{df(net_k)}{dnet_k} = \delta_k = y_k - y_{真实} \\ \end{aligned}$

答：

e = - \frac{1}{n} \sum_{i = 1}^{n} (y_{真 实} \ln y_{输 出} + (1 - y_{真 实}) \ln (1 - y_{输 出}))

$e = - \frac {1}{n} \sum_{i=1}^n (y_{真实}\ln{y_{输出}} + (1-y_{真实})\ln{(1-y_{输出})})$

结学

我们如何设计新的损失函数？
答：我们倒着推导：
首先找到loss跟误差项的关系；
然后根据该关系以及loss的公式，设计希望的误差项公式；
最后根据梯度与误差项的公式，推导出损失函数的公式。
如何加快二分类的训练速度？
答：使用新的损失函数，使loss跟收敛速度成正比

任务：判断性别Demo使用交叉熵损失函数

请实现“使用交叉熵损失函数”的代码
- 实现_computeLoss函数
- 修改输出层误差项的计算

答：待实现的代码为：CrossEntropyLoss_gender，实现后的代码为：CrossEntropyLoss_gender_answer

请每个同学运行代码，并与之前的代码NeuralNetwork_train_fix_zeroMean_answer_fix比较，看下：
- loss的训练速度是否加快？
- 是否在loss很大时训练速度也很快？

答：我们取20轮的训练结果

之前的代码的运行结果：

[ 'loss: ', 0.4507304592177789 ]
[ 'loss: ', 0.42877150239298367 ]
[ 'loss: ', 0.4003410570050336 ]
[ 'loss: ', 0.36471054740582803 ]
[ 'loss: ', 0.32348350190262276 ]
[ 'loss: ', 0.28148842822336106 ]
[ 'loss: ', 0.24435904667566208 ]
[ 'loss: ', 0.21478940821264678 ]
[ 'loss: ', 0.19217920769398236 ]
[ 'loss: ', 0.1746959045869208 ]
[ 'loss: ', 0.16069147885466947 ]
[ 'loss: ', 0.14903993518214445 ]
[ 'loss: ', 0.13904224985035976 ]
[ 'loss: ', 0.13027401434711444 ]
[ 'loss: ', 0.12247365805566274 ]
[ 'loss: ', 0.11547411658524662 ]
[ 'loss: ', 0.10916376857366585 ]
[ 'loss: ', 0.1034647748090702 ]
[ 'loss: ', 0.09832137076163855 ]
[ 'loss: ', 0.09369385876122124 ]

现在的代码的运行结果：

[ 'loss: ', 0.9942633398183269 ]
[ 'loss: ', 0.6659776522867806 ]
[ 'loss: ', 0.49140689993232145 ]
[ 'loss: ', 0.37709033494651706 ]
[ 'loss: ', 0.2994042613488786 ]
[ 'loss: ', 0.22748275377361313 ]
[ 'loss: ', 0.178710734329234 ]
[ 'loss: ', 0.14814081504087312 ]
[ 'loss: ', 0.1262728567509965 ]
[ 'loss: ', 0.10981773645519985 ]
[ 'loss: ', 0.09701072087557354 ]
[ 'loss: ', 0.08678048289782145 ]
[ 'loss: ', 0.07843471667890223 ]
[ 'loss: ', 0.07150614449993825 ]
[ 'loss: ', 0.06566841165919438 ]
[ 'loss: ', 0.06068705773306658 ]
[ 'loss: ', 0.05638955210782751 ]
[ 'loss: ', 0.05264627797401171 ]
[ 'loss: ', 0.049358078224151274 ]
[ 'loss: ', 0.04644787505022075 ]