深度学习基础课:全连接层的梯度检查
大家好~我开设了“深度学习基础班”的线上课程,带领同学从0开始学习全连接和卷积神经网络,进行数学推导,并且实现可以运行的Demo程序
线上课程资料:
本节课录像回放1
本节课录像回放2
本节课录像回放3
加QQ群,获得ppt等资料,与群主交流讨论:106047770
本系列文章为线上课程的复盘,每上完一节课就会同步发布对应的文章
本文为第四节课:“全连接层的梯度检查”的复盘文章
本课程系列文章可进入索引查看:
深度学习基础课系列文章索引
回顾相关课程内容
-
第二节课“判断性别”Demo需求分析和初步设计(下1)
- 求损失函数的极小值点的梯度下降公式是什么?
-
第三节课:全连接层的前向和后向传播推导(下)
- 反向传播算法计算的结果是什么?
- 计算梯度有什么用?
-
第二节课“判断性别”Demo需求分析和初步设计(下1)
- 损失函数的表达式是什么?
- 随机梯度下降算法是什么?
- 随机梯度下降公式是什么?
- 求损失函数的极小值点的梯度下降公式是什么?
为什么要学习本课
- 如何验证反向传播计算的梯度是否正确?
- 我们是如何验证的?
答:验证过程为:因为NeuralNetwork_train_answer->train函数打印的loss的结果与判断性别Demo的NeuralNetwork_train_before->train函数打印的loss一样,所以说明代码正确,通过了运行测试 - 还有其它办法吗?
- 我们是如何验证的?
主问题:如何以最小的误差计算导数?
任务:实现导数的计算
- 导数的定义是什么?
\( f'(x) = \lim_{h \to 0} ? \)
答:
- 请实现导数的计算
答:待实现的代码:Diff1
实现后的代码:Diff1_answer
任务:计算函数的导数
- 请用刚刚写的代码计算下面的函数在x=2的导数,查看是否有误差?
\( f(x)=x^2 + 3x \)
答:实现后的代码:Diff1_compute_answer- h如果太小(如1e-15),误差是否会增加?
答:会 - 为什么?
答:因为计算机的浮点数误差的原因,h太小的话(比如1e-15)会造成计算结果上的误差,所以我们一般用[1e-4,1e-7]之间的数值。 我们这里使用1e-4
- h如果太小(如1e-15),误差是否会增加?
任务:实现改进的导数的计算
-
如何修改导数的定义公式\(f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}\),从而减小误差?
- 如该图所示,红色实线的斜率是真实的导数

- 蓝色虚线的斜率是目前求得的导数
- 为什么?
- 绿色虚线的斜率是否更接近真实导数?
- 如何修改导数的定义公式为绿色的虚线?
答:修改后的公式为:
- 如该图所示,红色实线的斜率是真实的导数
- 请实现改进的导数的计算
答:待实现的代码:Diff2
实现后的代码:Diff2_answer
任务:计算函数的导数
- 请用刚刚写的代码计算同样的函数在x=2的导数,查看误差是否变小了?
答:实现后的代码:Diff2_compute_answer
运行代码后,发现误差确实更小了
主问题:梯度检查的思路是什么?
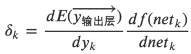
- 梯度\(\frac{dE}{dw_{ji}}\)是否为导数?
答:是 - 通过导数定义的公式\(f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x - h)}{2h}\)计算梯度的公式是什么?
答:
- 如何用该公式检查梯度?
答:我们使用该公式来计算梯度值;
然后将其与后向传播计算的梯度值进行比较。
如果两者的误差小于1e-4,那么就说明后向传播的代码是正确的。
主问题:如何对输出层进行梯度检查?
- 对输出层进行梯度检查的步骤是什么?
答:
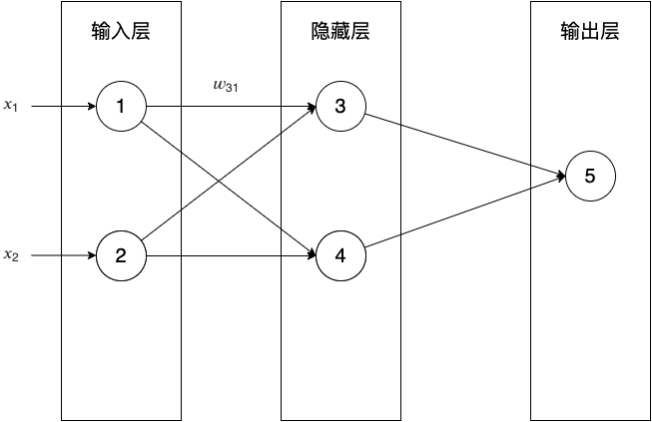
1、使用一个样本d进行前向传播和后向传播,这样就能得到输出层的一个神经元k的梯度
2、将神经元k的一个权重值𝑤_𝑗𝑖加上一个很小的值𝜀(1e-4 ),重新计算神经网络在这个样本d的E:E(𝑤_𝑗𝑖+𝜀)
3、将神经元k的一个权重值𝑤_𝑗𝑖 减去一个很小的值𝜀(1e-4 ),重新计算神经网络在这个样本d的E:E(𝑤_𝑗𝑖−𝜀)
4、根据导数定义公式计算出期望的梯度值,和第一步获得的梯度值进行比较,误差应该小于1e-4
5、重复上面的过程,对输出层的每个神经元的每个权重进行检查
- 在通过后向传播计算梯度的误差项时,n是多少?

答:因为只用了一个样本,所以n是1
任务:实现输出层的梯度检查
- 请实现输出层的梯度检查
- 实现前面4个步骤
答:待实现的代码:OutputLayerGradientCheck
实现后的代码:OutputLayerGradientCheck_1_4_answer - 实现所有步骤
答:实现后的代码:OutputLayerGradientCheck_5_answer
- 实现前面4个步骤
- 请每个同学都运行代码,看下是否通过了检查
答:通过了检查。运行结果如下:

主问题:如何对隐藏层进行梯度检查?
-
对隐藏层进行梯度检查的步骤是什么?
答:步骤与对输出层进行梯度检查相同 -
在通过后向传播计算隐藏层的梯度的误差项时,需要输出层的误差项,它是多少?
即:\( \begin{aligned} \overrightarrow{\delta_{隐藏层}} &=\begin{bmatrix} \delta_{3} \\ \delta_{4} \\ \end{bmatrix}\\ &= \begin{bmatrix} \overrightarrow{\delta_{输出层}} \cdot W_{输出层_{1列}} \;\; \frac{df(net_3)}{dnet_3} \\ \overrightarrow{\delta_{输出层}} \cdot W_{输出层_{2列}} \;\; \frac{df(net_4)}{dnet_4} \\ \end{bmatrix} \end{aligned} \)中的\(\overrightarrow{\delta_{输出层}} = ?\)- 损失函数E应该设计成什么,以及输出层应该选择什么激活函数(sigmoid or linear),才能使输出层的误差向量的值全为1?
答:
- 损失函数E应该设计成什么,以及输出层应该选择什么激活函数(sigmoid or linear),才能使输出层的误差向量的值全为1?
输出层的误差项公式为:
- 现在输出层的激活函数使用linear,那么隐藏层的激活函数也必须是linear吗?
答:不需要
任务:实现隐藏层的梯度检查

- 请实现隐藏层的梯度检查
答:待实现的代码:HiddenLayerGradientCheck
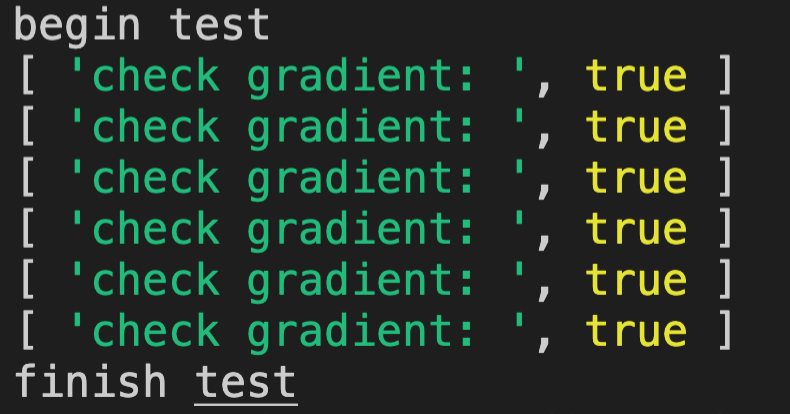
实现后的代码:HiddenLayerGradientCheck_answer - 请每个同学都运行代码,看下是否通过了检查
答:通过了检查。运行结果如下:
任务:整合全连接层的梯度检查
-
请整合输出层和隐藏层的梯度检查
答:待实现的代码:LinearLayerGradientCheck
实现后的代码:LinearLayerGradientCheck_answer -
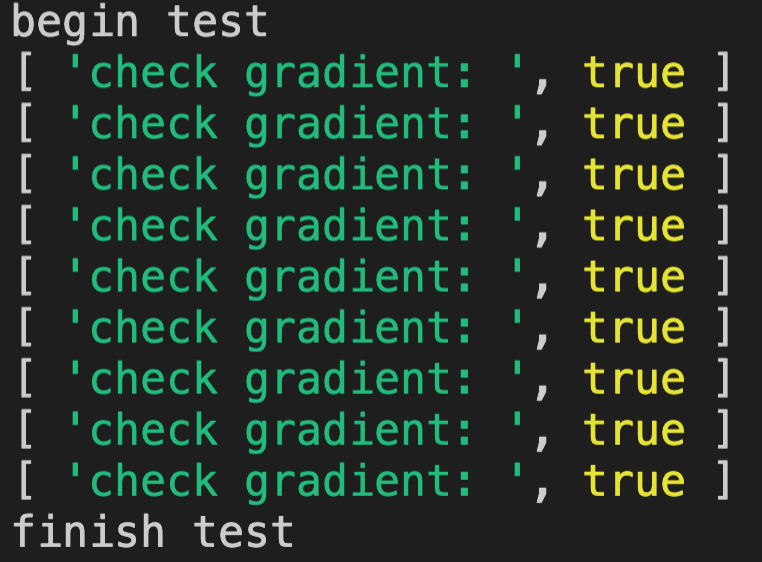
请每个同学都运行代码,看下是否通过了检查
答:通过了检查。运行结果如下:
总结
- 请总结本节课的内容?
- 请回答所有主问题?




 浙公网安备 33010602011771号
浙公网安备 33010602011771号