深度学习基础课：全连接层的前向和后向传播推导（下）

大家好~我开设了“深度学习基础班”的线上课程，带领同学从0开始学习全连接和卷积神经网络，进行数学推导，并且实现可以运行的Demo程序

线上课程资料：
本节课录像回放1
本节课录像回放2
本节课录像回放3

加QQ群，获得ppt等资料，与群主交流讨论：106047770

本系列文章为线上课程的复盘，每上完一节课就会同步发布对应的文章

本文为第三节课：“全连接层的前向和后向传播推导（下）”的复盘文章

本课程系列文章可进入索引查看：
深度学习基础课系列文章索引

回顾相关课程内容
主问题：如何推导全连接层的后向传播？
- 为什么要推导全连接层的后向传播？
- 主问题：如何推导全连接层的后向传播？
任务：实现全连接层的后向传播
任务：使用全连接层实现“判断性别Demo”
总结
参考资料

回顾相关课程内容

第二节课“判断性别”Demo需求分析和初步设计（下1）
- 损失函数的表达式是什么？
- 随机梯度下降算法是什么？
- 随机梯度下降公式是什么？
- 求损失函数的极小值点的梯度下降公式是什么？
第二节课“判断性别”Demo需求分析和初步设计（下2）
- 对于“判断性别”的Demo，𝐸可以是什么函数？
- 什么是训练?
- 如何求梯度？
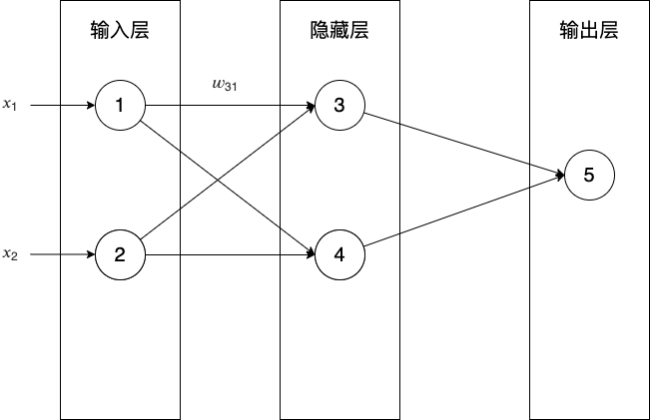
  - 如何求\(\frac{dE}{dw_{53}}\)？
  - 如何求\(\frac{dE}{dw_{31}}\)？

主问题：如何推导全连接层的后向传播？

为什么要推导全连接层的后向传播？

通过训练，我们希望得到什么？
为了得到更新后的权重和偏移，需要知道什么？
“判断性别Demo”是如何实现训练的？
梯度的数量太多，导致计算很臃肿，如何优化？
如果增加隐藏层中的神经元数量，是否会修改梯度计算的代码？
如何才能不修改代码，只调整参数即可？

答：将梯度向量化

回顾计算梯度的代码，有哪些是重复的计算？
能否在梯度向量化公式中，将重复计算提出来？

答：参考一文搞懂反向传:

其实对于已经计算完毕的节点我们完全可以直接拿来用，因此我们可以重新看待这个问题，从后往前更新。先更新后边的权重，之后再在此基础上利用更新后边的权重产生的中间值来更新较靠前的参数。
这个中间变量就是本课要引入的误差项

因此，我们需要先计算出输出层的误差项；
再根据它来计算出隐藏层的误差项；
最后根据它们分别计算出输出层和隐藏层的梯度

主问题：如何推导全连接层的后向传播？

输出层神经元的误差项是什么？
答：
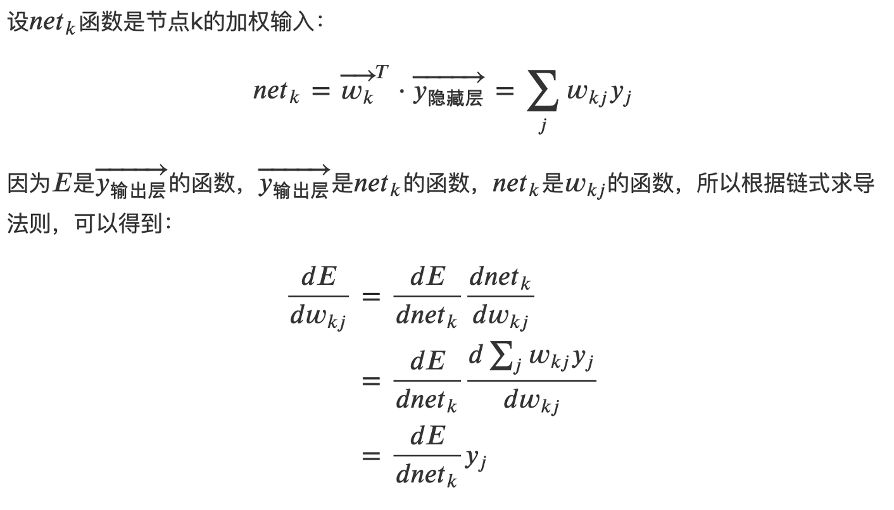
隐藏层神经元的误差项是什么？
答：
所以每层神经元的误差项计算公式都是什么？
答：

\[\delta_j=\frac{dE}{dnet_j} \]

每个神经元权重\(𝑤_{ji}\)的梯度（ \(𝑤_{ji}\)表示从神经元i接到神经元j的权重）是什么？
答：

\[\frac{dE}{dw_{ji}}=\delta_j a_i\\ 其中a_i为神经元i的输出 \]

所以求梯度的问题转换为求什么？
答：求误差项
如何计算输出层神经元的误差项： \(\delta_k=\frac{dE}{dnet_k}\) ？
答：
对于下图的神经网络，输出层的误差向量是什么？

答：

\[\overrightarrow{\delta_{输出层}} = \begin{bmatrix} \delta_{5} \\ \end{bmatrix} \]

如何计算隐藏层神经元的误差项： \(\delta_j=\frac{dE}{dnet_j}\) ？
答：
对于下图的神经网络，隐藏层的误差向量是什么？

答：

\[\begin{aligned} W_{输出层} &=\begin{bmatrix} w_{53}, w_{54}, w_{b_5} \\ \end{bmatrix} \\ \overrightarrow{\delta_{隐藏层}} &=\begin{bmatrix} \delta_{3} \\ \delta_{4} \\ \end{bmatrix}\\ &= \begin{bmatrix} \overrightarrow{\delta_{输出层}} \cdot W_{输出层_{1列}} \;\; \frac{df(net_3)}{dnet_3} \\ \overrightarrow{\delta_{输出层}} \cdot W_{输出层_{2列}} \;\; \frac{df(net_4)}{dnet_4} \\ \end{bmatrix} \end{aligned} \]

该向量公式同样适用于输出层有多个神经元的情况

更新后的输出层和隐藏层的梯度下降算法是什么？
答：更新前的算法公式如下：

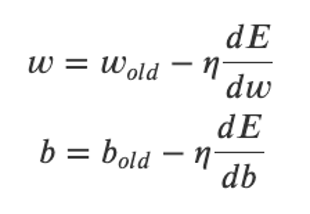
更新后的输出层和隐藏层的算法公式如下：
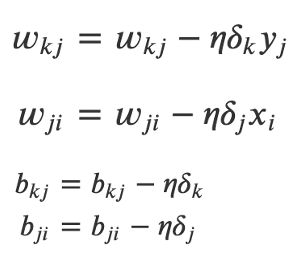
对于下图的神经网络，如何向量化输出层和隐藏层的梯度下降算法？

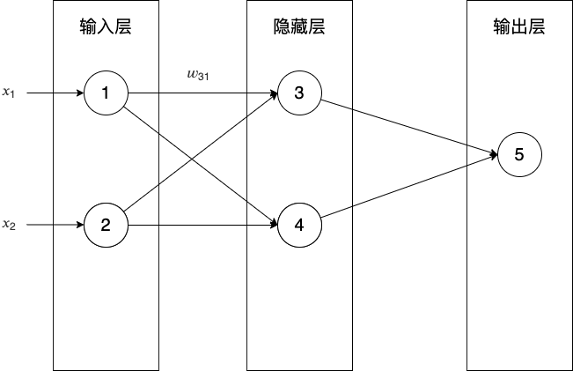
答：输出层梯度下降算法向量化公式如下：

隐藏层梯度下降算法向量化公式如下：
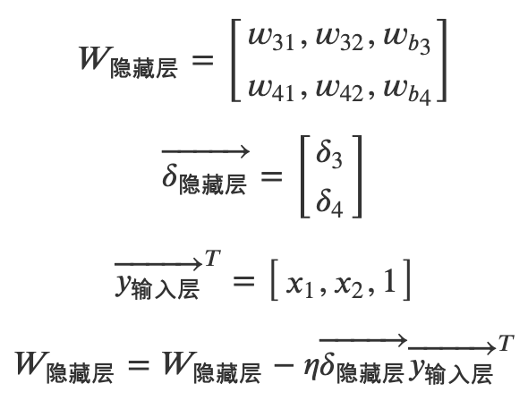
什么是后向传播算法？
答：先计算输出层的误差项，然后反向依次计算每层的误差项直到与输入层相连的层，最后根据每层的误差项和输入得到每层的梯度

任务：实现全连接层的后向传播

请实现全连接层的后向传播的代码（损失函数和激活函数与判断性别Demo一样）
答：待实现的代码：NeuralNetwork_train
实现后的代码：NeuralNetwork_train_answer
使用判断性别Demo的神经网络结构，运行代码，通过运行测试

答：因为NeuralNetwork_train_answer->train函数打印的loss的结果与判断性别Demo的NeuralNetwork_train_before->train函数打印的loss一样，所以说明代码正确，通过了运行测试

任务：使用全连接层实现“判断性别Demo”

请参考判断性别Demo的代码NeuralNetwork_train_fix_zeroMean_answer_fix，整合全连接层的前向、后向传播的代码
答：待实现的代码：LinearLayer
实现后的代码：LinearLayer_answer
使用判断性别Demo的神经网络结构，运行代码，通过“判断性别Demo”的运行测试

答：运行代码LinearLayer_answer，运行结果是loss收敛，并且正确地推理出两个样本的性别，从而通过了运行测试