深度学习基础课: “判断性别”Demo需求分析和初步设计(下1)
大家好~我开设了“深度学习基础班”的线上课程,带领同学从0开始学习全连接和卷积神经网络,进行数学推导,并且实现可以运行的Demo程序
线上课程资料:
本节课录像回放
加QQ群,获得ppt等资料,与群主交流讨论:106047770
本系列文章为线上课程的复盘,每上完一节课就会同步发布对应的文章
本文为第二节课:“判断性别”Demo需求分析和初步设计(下1)的复盘文章
本课程系列文章可进入索引查看:
深度学习基础课系列文章索引
回顾相关课程内容
- 第二节课:“判断性别”Demo需求分析和初步设计(中)
- 什么是神经网络 ?
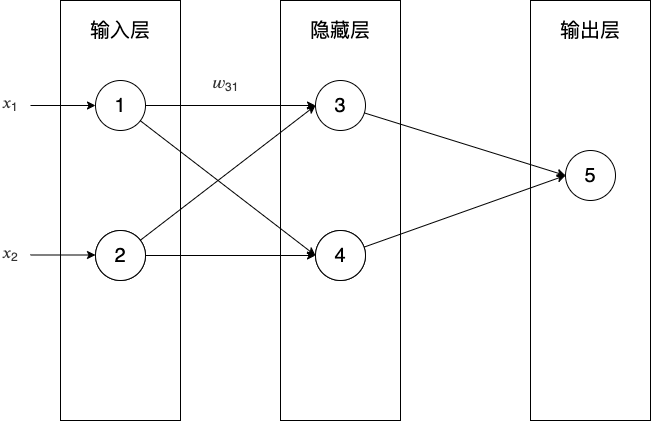
- 为什么引入神经网络?
- 前向传播算法包括哪些步骤?
- 什么是神经网络 ?
主问题:什么是损失函数
为什么引入损失函数?
- 虽然神经网络的未知量的数量比起神经元来说更多,但如果推理的样本数量比神经网络的未知量的数量更多时,该怎么办?
- 继续增加神经网络中的权重、偏移数量(如增加层、增加每层的神经元)?
答:不能,因为:
这会增加计算成本;
样本数量可以任意多,但无法无限地增加神经网络中的权重、偏移数量
所以应该保持神经网络中的权重、偏移数量不变
- 继续增加神经网络中的权重、偏移数量(如增加层、增加每层的神经元)?
- 在训练后仍然会得到一组权重、偏移,但在推理阶段对于每个样本推理的输出值仍然等于真实值吗?
答:不等于 - 我们希望的结果是什么?
答:每个样本推理的输出值尽量接近真实值 - 因此,在训练时需要得到一组合适的权重、偏移,使得每个样本推理的输出值尽量接近真实值
- 那么,如何具体判断得到的一组权重、偏移是合适的呢?
答:需要引入损失函数𝐸,用来在训练阶段度量在推理阶段的输出值和真实值的误差大小
什么是损失函数
- 损失函数的表达式是什么?
- 值是什么?
答:误差 - 自变量、常量分别是什么?
答:输出是自变量,真实值是常量 - 表达式是什么?
答:𝑒=𝐸(𝑦输出)
- 值是什么?
- 有了损失函数,如何具体判断得到的一组权重、偏移是合适的呢?
- 希望得到损失函数的最大值还是最小值?
答:最小值 - 此时的自变量(输出)就是合适的的值
- 输出跟权重、偏移是什么关系?
答: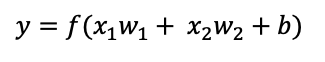
根据上面的公式可知是函数映射关系,其中前者是函数的值,后者是函数的自变量- 输入x是自变量还是常量?为什么?
答:输入x是常量。
因为损失函数用于在训练阶段确定合适的权重和偏移,而此时输入x是已知的(如为100个样本数据)
- 输入x是自变量还是常量?为什么?
- 损失函数的表达式更新为:𝑒=𝐸(𝑤,𝑏)
- 所以如何具体判断得到的一组权重、偏移是合适的呢?
答:求出损失函数的最小值,此时作为自变量的权重、偏移就是合适的
- 希望得到损失函数的最大值还是最小值?
主问题:什么是随机梯度下降
-
如何用数值分析的方法求一个函数的最小值点?
答: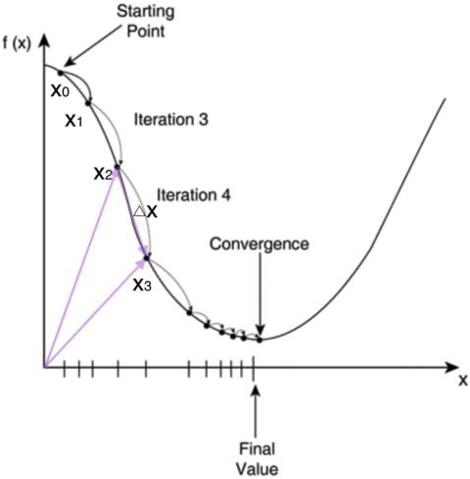
首先,我们随便选择一个点开始,比如上图的𝑥0。接下来,每次迭代修改𝑋为𝑥1,𝑥2,𝑥3......经过数次迭代后最终达到函数最小值点。
你可能要问了,为啥每次修改𝑋,都能往函数最小值那个方向前进呢?这里的奥秘在于,我们每次都是向函数𝑦=𝑓(𝑥) 的梯度的相反方向来修改𝑋。
什么是梯度呢?梯度是一个向量,它指向函数值上升最快的方向。显然,梯度的反方向当然就是函数值下降最快的方向了。 -
求出来的是极小值点还是最小值点?
答:极小值 -
如何求最小值点?
答:再取多组值来判断(可升级为小批量随机梯度下降) -
所以,求一个函数的极小值点的算法(梯度下降算法)总结成公式是什么?
答:
-
求损失函数的极小值点的梯度下降算法总结成公式是什么?
答: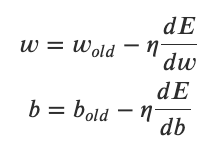




 浙公网安备 33010602011771号
浙公网安备 33010602011771号