[XILINX-ACAP] 矩阵乘法MatMult: single core

ref:

https://github.com/Xilinx/Vitis-Tutorials/blob/2021.2/AI_Engine_Development/Feature_Tutorials/07-AI-Engine-Floating-Point/MatMult/aie/aie_kernels/matmult_float.cpp

int 的mac 计算patten比较绕，遂扒了一个tutorials里FP的例子, 简单些。

0. Design idea

由底向上的设计思路：

第一步：看FP MAC向量计算的能力，以及最多能放多少个float到向量寄存器里。

第二步：在内层循环做到LOAD 数<=MAC 数，保证MAC始终处于工作状态。

第三步：kernel计算能力和DMA带宽匹配确定window size。

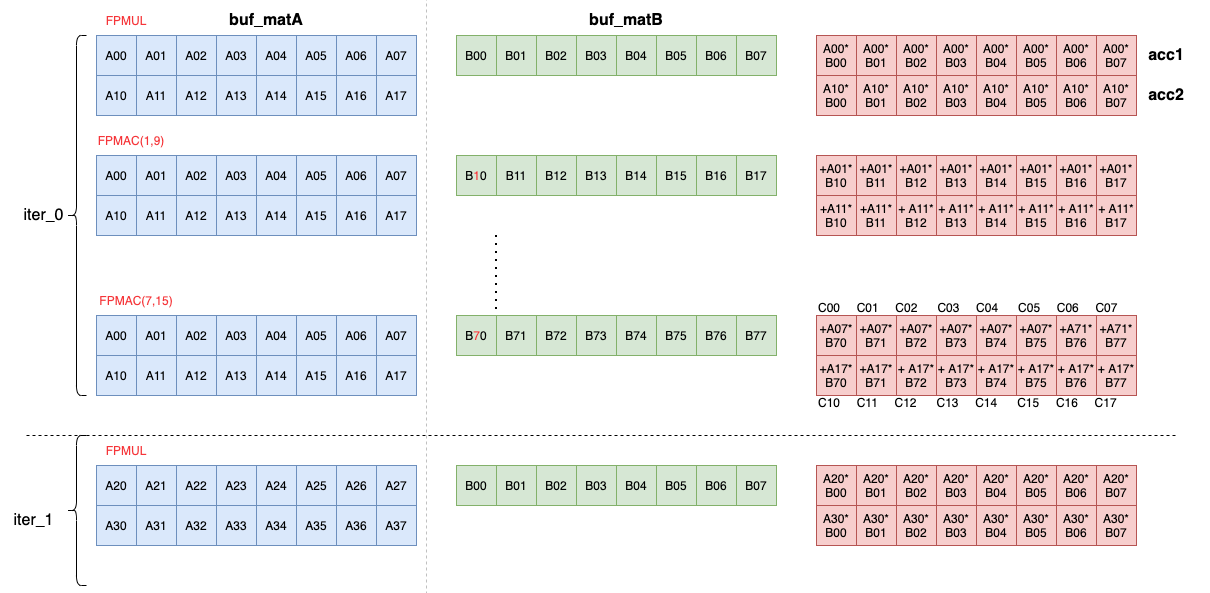
1. MAC  

Arch 文档告诉我们，8 lanes 的单精度浮点乘法。查intrinsic网页，得到fpmul 的计算pattern如下（link）：

for (i = 0 ; i < 8 ; i++)
  ret[i] =  xbuf[xstart + xoffs[i]] * zbuf[zstart + zoffs[i]]

tutorials里用的参数和对应的pattern是从A取1个元素，广播乘以B的每个元素。

acc1 = fpmul(buf_matA,0,0x00000000,buf_matB,0,0x76543210)
//以下仅仅为示意，没有重载[] 运算符.
acc1[0] = buf_matA[0] * buf_matB[0];
acc1[1] = buf_matA[0] * buf_matB[1];
acc1[2] = buf_matA[0] * buf_matB[2];
acc1[3] = buf_matA[0] * buf_matB[3];
acc1[4] = buf_matA[0] * buf_matB[4];
acc1[5] = buf_matA[0] * buf_matB[5];
acc1[6] = buf_matA[0] * buf_matB[6];
acc1[7] = buf_matA[0] * buf_matB[7];

 

2. Loop

 用了两个acc, 循环体内A只LOAD一次， 总共2行(2x8),  每次MAC前先LOAD 1行B(1x8)，1个LOAD B 可供两个MAC 消耗，总的来说是LOAD少MAC多。这样循环体内就算出两行C矩阵。

循环间更新A指针到新行，B指针折回。

for (unsigned int i=0;i<F_Ra/2;i++)  // Each iteration computes 2 rows of C
   chess_prepare_for_pipelining
   chess_loop_range(8,)
   {
     FPMUL;
     FPMAC(1,9);
     FPMAC(2,10);
     FPMAC(3,11);
     FPMAC(4,12);
     FPMAC(5,13);
     FPMAC(6,14);
     FPMAC(7,15);

     buf_matA = window_readincr_v16(matA); // reads the next 2 rows of A
     window_decr_v8(matB,8); // reset B pointer
     window_writeincr(matC,acc1); // Writes 1 row of C
     window_writeincr(matC,acc2); // Writes the next row of C
   }

 

 3 Overview

假设有矩阵乘 C = A x B,   C为M行N列, A为M行K列。

• 并行度分配

	M	N	K
one MAC	1	8	1
two MAC	x2	--	--
loop body	--	--	x8
loop	x(M/2)	--	--
overall	M	8	8

那么该kernel函数处理的是 A 矩阵尺寸为 Mx8，B矩阵 8x8,  得到C矩阵Mx8 .

• 计算量

C矩阵有8x8 个元素，每个元素需要8个float乘加得到。那么对float乘的需求就是 workload = Mx8x8.

考虑到MAC的计算能力是 8 lanes，可以认为是cal_power = 8 float32 x float32 per cycle per core.

那么单核理论计算事件就是 workload/cal_power = (Mx8x8)/8 = 8*M cycles.

• 带宽

进到AIE Data Memory 的stream为2x32bits(即4B/cycle 每条stream)。假设2条stream通路分别用来传输A和B。

加载A 的cycle = (M*8*sizeof(float32)) / (4B/cycle) = 8*M cycles

加载B 的cycle = (8*8*sizeof(float32)) / (4B/cycle) = 64 cycles

从AIE Data Memory 到stream 也是两条通路，各4B/cycles，这里假设输出C输出后的stream没有merge。

那么输出C的cycles = (M*8*sizeof(float32)) / (4B/cycle) = 8*M cycles

• 计算/带宽

8*M / max(trans(A), trans(B), trans(C))

如果max(trans(A), trans(B), trans(C)) = 8*M, 那么计算cycle(8*M) = 传输cycle(8*M)， 匹配

如果=64, 那么计算/传输 = (8*M)/64， 就需要8*M>=64, 才能满足计算带宽匹配需求。