NumPy的transpose方法详解

在上一篇的数组转置和换轴之中，换轴的时候书本上用到了 transpose 这个方法，然后数组就莫名其妙的发生了变化，而且根本让人看不懂。于是我就去百度了很久关于 transpose 函数的用法。 总结了以下心得。

一开始我以为 transpose方法只是单纯的把三维数组的每个基层元素的x和y对调了以下，后来发现错的离谱。

注：下面四个图均有一点小错误，已经做出了详细的解释，谨慎看。

在NumPy文档中，对numpy.transpose 走了一些解释，他的作用是改变序列，下面是一些文档的栗子：

x = np.arange(4).reshape((2,2))

#输出
array([[0, 1],
       [2, 3]])

import numpy as np
x.transpose()

#输出
array([[0, 2],
       [1, 3]])

对于二维的 ndarray来说，transpose在不指定参数时默认是矩阵转置。如果制定了参数，就会有如下的相应结果：

x.transpose((0,1))

#结果
# x 没有变化
array([[0, 1],
       [2, 3]])

x.transpose((1,0))


#结果
# x 转置了
array([[0, 2],
       [1, 3]])

为了方便理解

先写出这样子的表达式

x[0][0] == 0
x[0][1] == 1
x[1][0] == 2
x[1][1] == 3

可以看到和 x数组的每个位置的对应关系了。

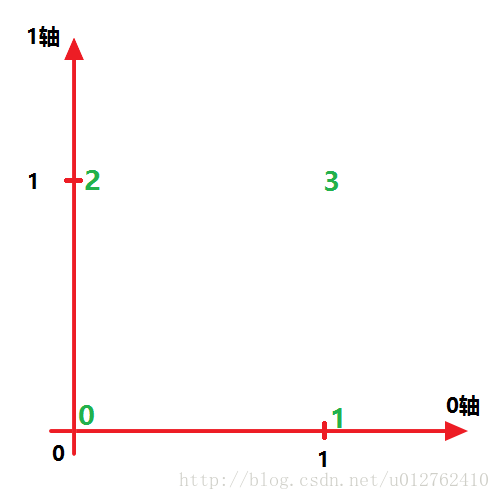
设第一个方括号 "[ ]"为0轴 第二个方括号为 1轴 ，就可以建立0-1的坐标系了。

由于是网上找的图，这张图画错了，2 和 1 的位置应该换一下。

能清晰的看清每个基层元素的位置。

因为 x.transpose((0,1)) 表示按照原坐标轴改变序列，也就是保持不变，所以最后的结果不变

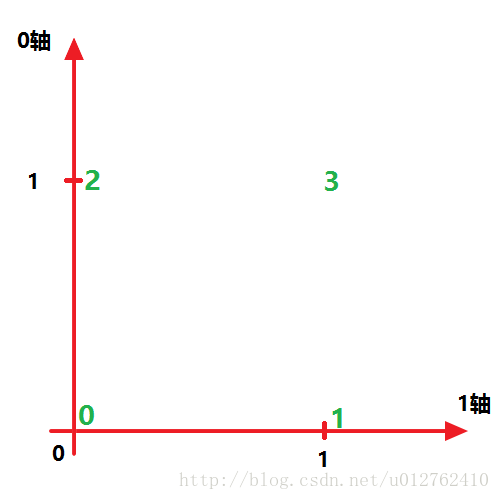
而 x.transpose((1,0)) 表示交换 ‘0轴’ 和 ‘1轴’，所以就得到如下图所示结果：

该图也是，2 和 1 应该换一下

无论什么时候，都记住第一个方括号是0轴 第二个方括号是1轴，这样就不会乱，transpose的关系就很清晰了。

难点来了。 三维数组的转置。

import numpy as np

# A是array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15])
A = np.arange(16)

# 将A变换为三维矩阵
A = A.reshape(2,2,4)
print(A)


#结果
A = array([[[ 0,  1,  2,  3],
            [ 4,  5,  6,  7]],

           [[ 8,  9, 10, 11],
            [12, 13, 14, 15]]])

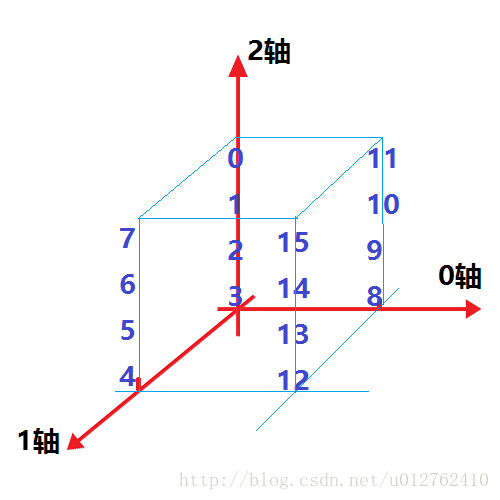
我们对上述的A表示成如下三维坐标的形式：

该图的 0,1,2,3 写反了， 应是3,2,1,0 （自上向下）

然后下面的转变就会很好理解了。

A.transpose((0,1,2))  #保持A不变
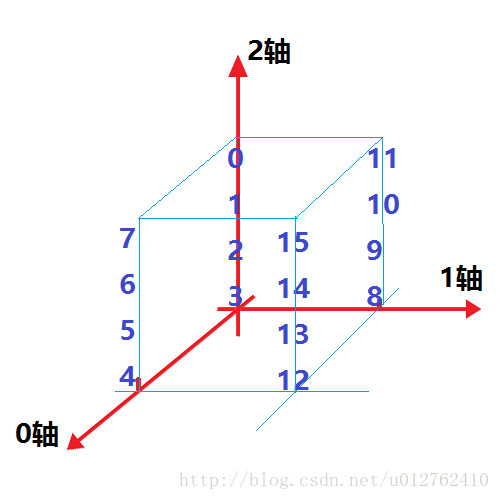
A.transpose((1,0,2))  #将 0轴 和 1轴 交换

该图的 0,1,2,3 写反了， 应是3,2,1,0 （自上向下）

把 0轴 和 1轴 交换

这时候这个 transpose 就已经被容易理解了。

参考原文链接：https://blog.csdn.net/u012762410/article/details/78912667