C++解说无穷小量与无穷大量【C++解说微积分】
数学基础:
(1)无穷小量
对函数 $f(x)$,假设$x$趋于$x_0$时函数$f(x)$的极限为0,则称函数$f(x)$为$x$趋于$x_0$时的无穷小量,也叫无穷小。
(2)无穷大量
对函数 $f(x)$,假设$x$趋于$x_0$时函数$f(x)$的绝对值无限增大,则称函数$f(x)$为$x$趋于$x_0$时的无穷大量,也叫无穷大,也可以说极限不存在。
(3)无穷小的比较
设$\alpha$、$\beta$为自变量的同一变化过程中的无穷小,且$\alpha\neq0$.
若$lim\frac{\beta}{\alpha}=0$,则称$\beta$是比$\alpha$高阶的无穷小,记作$\beta=0(\alpha)$;
若$lim\frac{\beta}{\alpha}=\infty$,则称$\beta$是比$\alpha$低阶的无穷小;
若$lim\frac{\beta}{\alpha}=C\neq0$,则称$\beta$是$\alpha$的同阶无穷小;
特别当$C=1$时,则称$\beta$是$\alpha$的等价无穷小,记作$α~β$;
若$lim\frac{\beta}{\alpha^k}=C\neq0$,则称$\beta$是$\alpha$的$k$阶无穷小。
数学求解:
比较以下无穷小量的阶。
(1)当$x\to2$时,$x-2$与$x^2-4$;
(2)当$x\to1$时,$x-1$与$x^2-x$;
(3)当$x\to\infty$时,$\frac{2}{x}$与$\frac{3}{x^2}$;
解:
(1)因为$x$趋于2时:
$$
\lim_{x\to2}\frac{x-2}{x^2-4}=\lim_{x\to2}\frac{x-2}{(x-2)(x+2)}=\lim_{x\to2}\frac{1}{x+2}=\frac{1}{4}
$$
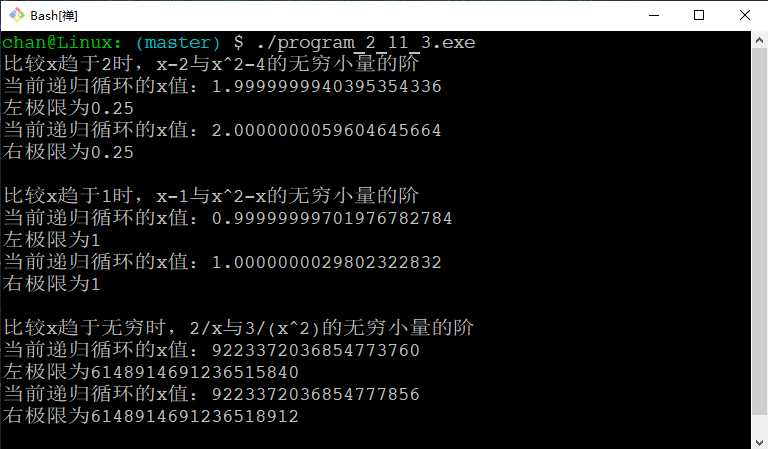
所以$x$趋于2时,$x-2$与$x^2-4$同阶无穷小。
(2)因为$x$趋于1时:
$$
\lim_{x\to1}\frac{x-1}{x^2-x}=\lim_{x\to1}\frac{x-1}{x(x-1)}=\lim_{x\to1}\frac{1}{x}=1
$$
所以$x$趋于1时,$x-1$与$x^2-x$同阶无穷小。
(1)因为$x$趋于$\infty$时:
$$
\lim_{x\to\infty}\frac{\frac{2}{x}}{\frac{3}{x^2}}=\lim_{x\to\infty}\frac{2x}{3}=\infty
$$
所以$x$趋于$\infty$时,$\frac{2}{x}$是比$\frac{3}{x^2}$低阶无穷小。
C++代码:
1 /** 2 * @file program_2_11_3.cpp 3 * @brief 比较无穷小量的阶(1)当x->2时,x-2与x^2-4;(2)当x->1时,x-1与x^2-x;(3)当->∞时,2/x与3/x^2 4 * @author 禅元天道 chanyuantiandao@126.com 5 * @version 1.0.0 6 * @date 2021-12-25 7 */ 8 #include <iostream> 9 #include <cmath> 10 #include <iomanip> 11 12 using namespace std; 13 14 /** 15 * @brief 设置允许的误差值 16 */ 17 const double tininessValue = 0.000000001 * 0.000000001; 18 19 /** 20 * @brief 计算(x-2)/(x^2-4)的值 21 * @param x 因变量x的值 22 * @return 计算结果 23 */ 24 double getValue1(double x) 25 { 26 if(x == 2){ 27 cout << "分母值为0,计算失败!" << endl; 28 return 0; 29 } 30 return (x-2)/(pow(x, 2) - 4); 31 } 32 33 /** 34 * @brief 计算(x-1)/(x^2-x)的值 35 * @param x 因变量x的值 36 * @return 计算结果 37 */ 38 double getValue2(double x) 39 { 40 if(x == 1){ 41 cout << "分母值为0,计算失败!" << endl; 42 return 0; 43 } 44 return (x-1)/(pow(x, 2) - x); 45 } 46 47 /** 48 * @brief 计算(2/x)/(3/x^2)的值 49 * @param x 因变量x的值 50 * @return 计算结果 51 */ 52 double getValue3(double x) 53 { 54 if(x == 0){ 55 cout << "分母值为0,计算失败!" << endl; 56 return 0; 57 } 58 return (2/x)/(3/pow(x, 2)); 59 } 60 61 void printLimValue(const double trend, const double incrementValue, double (*pf)(double)) 62 { 63 64 //开始求左极限 65 double tempIncrementValue = incrementValue; 66 double x = trend - tempIncrementValue; 67 double yPre = 0; 68 double yNow = (*pf)(x); 69 70 while(x < trend) 71 { 72 tempIncrementValue /= 2; 73 x += (tempIncrementValue); 74 yPre = yNow; 75 yNow = (*pf)(x); 76 if(abs(yNow - yPre) < tininessValue){ 77 cout << setprecision(20) << "当前递归循环的x值:" << x << endl; 78 cout << "左极限为" << yNow << endl; 79 break; 80 } 81 } 82 83 84 //开始求右极限 85 tempIncrementValue = incrementValue; 86 x = trend + tempIncrementValue; 87 yPre = 0; 88 yNow = (*pf)(x); 89 90 while(x > trend) 91 { 92 tempIncrementValue /= 2; 93 x -= (tempIncrementValue); 94 yPre = yNow; 95 yNow = (*pf)(x); 96 if(abs(yNow - yPre) < tininessValue){ 97 cout << setprecision(20) << "当前递归循环的x值:" << x << endl; 98 cout << "右极限为" << yNow << endl; 99 break; 100 } 101 } 102 103 cout<<endl; 104 } 105 106 int main() 107 { 108 //求极限时,x的趋向值 109 //const double trend = 2; 110 //求极限时,x的初始增量值: 111 //const double incrementValue = 0.1; 112 113 cout << "比较x趋于2时,x-2与x^2-4的无穷小量的阶" << endl; 114 printLimValue(2, 0.1, getValue1); 115 116 cout << "比较x趋于1时,x-1与x^2-x的无穷小量的阶" << endl; 117 printLimValue(1, 0.1, getValue2); 118 119 cout << "比较x趋于无穷时,2/x与3/(x^2)的无穷小量的阶" << endl; 120 //注意在处理无穷大时,增量值不能设置的太小,否则会出现LLONG_MAX减去一个很小值后得到的结果在计算机表示还是LLONG_MAX的值,无法进入while循环 121 printLimValue(LLONG_MAX, 9999, getValue3); 122 123 return 0; 124 }
运行结果: