C++解说函数的极限【C++解说微积分】

数学基础：

极限的概念：如果有一个函数$f(x)$，若存在一个很小的数$\epsilon>0$和一个很大的数$N>0$，使得当$x>N$时，总会有$f(x)$和$A$的差的绝对值小于$\epsilon $ ，那么可以称函数$f(x)$在$x\rightarrow +\infty$时极限为$A$，记作：$$\lim_{x\rightarrow +\infty} f(x) = A$$

此外还有左极限、有极限的概念，如有需求请自行百度学习。

 

问题模型：

假设某种疾病的感染人数与天数的函数关系为：

$$f(d)=\frac{10^8}{7+3\times10^4\times e^{-d}}$$

现在需要计算以下两个数据：

1. 计算感染人数到达100万需要的天数
2. 计算如果不采取措施，最终的感染人数。

 

C++代码：

/**
 * @file main.cpp
 * @author 禅元天道 chanyuantiadnao@126.com
 * @date 2021-11-25 15:47
 * @brief C++计算数学中的极限问题（模拟疾病传播情况）。
**/
#include <iostream>
#include <math.h>

/**
 * @brief 设置一个允许误差值
**/
const double dTininessVal = 0.000001;

/**
 * @brief 获取函数C(d) = 10^8/(7+3*10^4*e^(-d))的计算结果
 * @param double d 函数中d的值
 * @return 函数的计算结果
**/
double getFuncValue(double d)
{
    return pow(10, 8) / (7 + 3 * pow(10, 4) * exp(-d));
}

int main(void) 
{
    int nD = 0;
    double dl = getFuncValue(nD);
    //判断人数没有达到100万人，则一直循环
    while (dl < 1000000)
    {
        nD++;
        dl = getFuncValue(nD);
    }
    std::cout << "达到100万人次需要" << nD << "天。" << std::endl;

    //前一天的人数
    double dlPre = 0;
    //当天的人数
    double dlNow = 0;
    dlNow = dl;
    while (dlNow - dlPre > dTininessVal)
    {
        dlPre = dlNow;
        nD++;
        dlNow = getFuncValue(nD);
    }
    std::cout << "达到极限的人数：" << dlNow << std::endl;
    std::cout << "达到极限的天数：" << nD << std::endl;
    return 0;
}

 

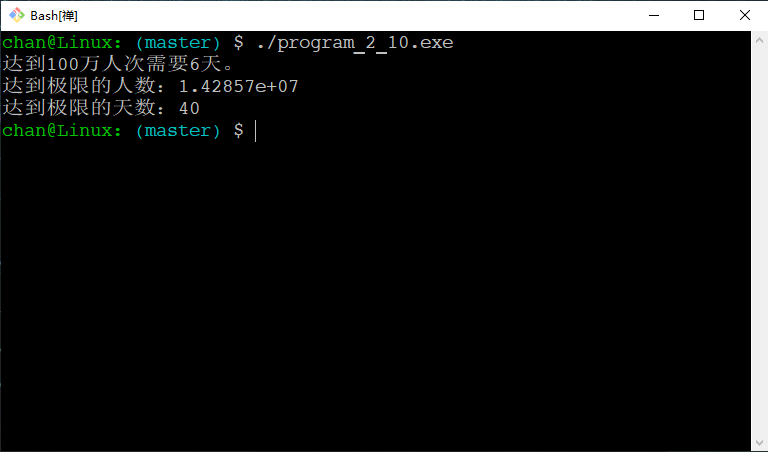
运行结果：