【数字电子技术基础】逻辑代数基础
三种基本运算
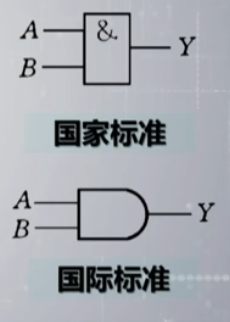
与
\(Y=A \space AND\space B = A\&B = A\cdot B = AB\)
逻辑与运算,实现与运算的电子器件成为与门。
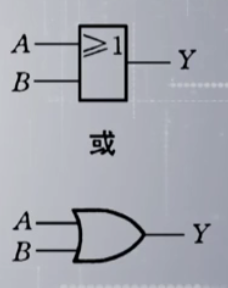
或
\(Y = A \space OR \space B = A + B\)
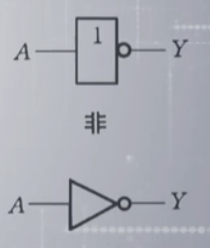
非
\(Y = NOT A = \overline{A} = A^\prime\)
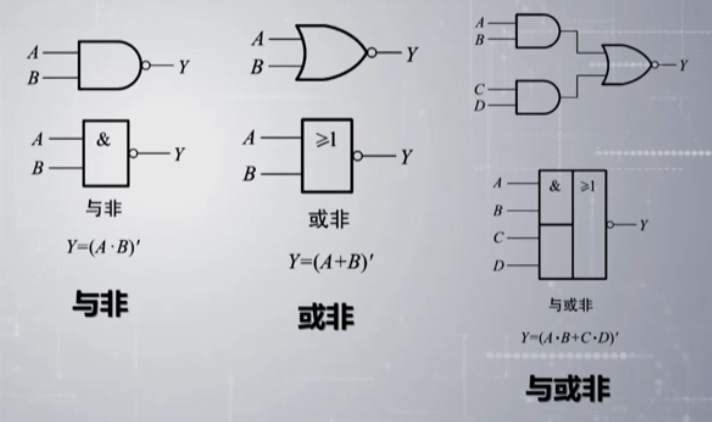
常用的复合逻辑运算
与非:\(Y=(A\cdot B)^\prime\)
或非:\(Y = (A+B)^\prime\)
与或非:\(Y = (A\cdot B + C \cdot D)^\prime\)
异或:\(Y=A\oplus B=(A^\prime \cdot B) + (A\cdot B^\prime)\) 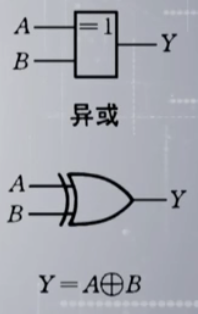
同或:\(Y=A\odot B=(A\oplus B)^\prime=((A^\prime\cdot B)+(A\cdot B^\prime))^\prime=(A^\prime\cdot B)^\prime\cdot(A\cdot B^\prime)^\prime\\=(A+B^\prime)\cdot(A^\prime+B)=A\cdot A^\prime + A\cdot B + A^\prime\cdot B^\prime + B\cdot B^\prime=A\cdot B + A^\prime \cdot B^\prime\)
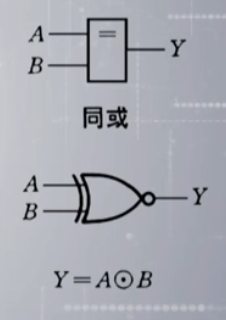
逻辑代数的基本公式和常用公式
基本公式
分配律:\(A+BC=(A+B)(A+C)\),\(A+BCD=(A+B)(A+C)(A+D)\)
反演律:\((AB)^\prime=A^\prime+B^\prime\),\((A+B)^\prime=A^\prime B^\prime\)
常用公式
- \(A+AB=A\)
\(A+AB=A(1+B)=A\)
- \(A(A+B)=A\)
\(AA+AB=A+AB=A(1+B)=A\)
- \(AB+AB^\prime=A\)
\(AB+AB^\prime=A(B+B^\prime)=A\)
- \(A+A^\prime B = A + B\)
\(A+A^\prime B=(A+A^\prime)(A+B)=A+B\)
-
\(AB+A^\prime C + BC=AB+A^\prime C\),\(AB+A^\prime C + BCD=AB + A^\prime C\)
-
\(A(AB)^\prime=AB^\prime\)\(A^\prime (AB)^\prime=A^\prime\)
\(A(AB)^\prime=A(A^\prime + B^\prime)=AA^\prime+AB^\prime\)
\(A^\prime (AB)^\prime=A^\prime(A^\prime+B^\prime)=A^\prime A^\prime+A^\prime B^\prime=A^\prime+A^\prime B^\prime=A^\prime(1+B^\prime)=A^\prime\)
逻辑代数的基本定理
代入定理
在任何一个包含A的逻辑式中,用另外一个逻辑式代替A的位置,则等式依然成立。这是数字电路可以模块化互联的理论基础。
因为逻辑式A无论多么复杂他的值仅仅只能是0或者1,同样其他逻辑式也是一样的,因此代替之后等式依然成立。
例如:\(A+BC=(A+B)(A+C)\),用CD代替C可得\(A+BCD=(A+B)(A+CD)=(A+B)(A+C)(A+D)\);
\((A\cdot B)^\prime=A^\prime + B^\prime\),用\(B\cdot C\)代替B可得\((A\cdot BC)^\prime=A^\prime + (BC)^\prime = A^\prime + B^\prime + C^\prime\).
反演定理
对于任意逻辑式\(Y\),要求他的反函数\(Y\Rightarrow Y^\prime\),则将‘与’改成‘或’,1改成0,需要注意的是不属于单变量的取反操作不改变,变换的顺序是先括号,然后与最后或。
例如:\(Y=A^\prime (B+C)+CD\),则\(Y^\prime = (A+B^\prime C^\prime)(C^\prime+D^\prime)=AC^\prime + AD^\prime + B^\prime C^\prime\).
对偶定理
逻辑式Y的对偶式\(Y\Rightarrow Y^D\),或变与,与变或,0变1,1变0。
若逻辑式\(F=G\),则\(F^D=G^D\).
例如:\(F=A+BC,G=(A+B)(A+C)\),有\(F^D=A^\prime (B^\prime + C^\prime)=A^\prime B^\prime+A^\prime C^\prime\)、\(G^D=A^\prime B^\prime+A^\prime C^\prime\),\(F^D=G^D\).
逻辑函数
逻辑函数的表示方法
真值表、逻辑图、逻辑式、波形图。
逻辑式
将输入输出之间的逻辑关系用与或非的运算式进行表示。例如\(Y=(AB+CD)^\prime\).
不同的逻辑式表示的可能是同一个真值表。
逻辑图
用逻辑图形符号表示逻辑运算关系。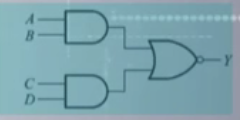
波形图
将输入变量所有取值组合与对应输出按时间顺序排列画成波形。
逻辑函数表示方法之间的转换
真值表->逻辑式
将Y=1的输入变量取值取出来,将取值组合与起来,其中取值为1的为原变量,取值为0的为反变量,最后将他们或起来即可。
例如:
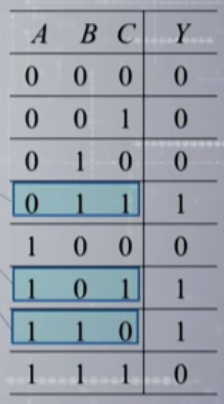
其中ABC取值为011,101,110的时候Y=1,则有\(Y=A^\prime BC+AB^\prime C + ABC^\prime\).
逻辑图->逻辑式
从输入到输出逐级写出每个图形符号对应的逻辑运算式。
把逻辑图看成一张图,则逻辑式的计算顺序按照拓扑排序结果进行计算。
例如:
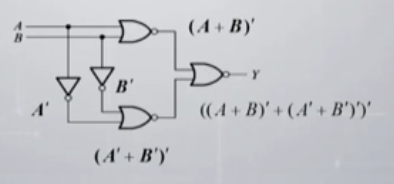
则有
\(Y=((A+B)^\prime +(A^\prime + B^\prime) ^\prime)^\prime=(A^\prime B^\prime + AB)^\prime=(A^\prime B^\prime)^\prime (AB)^\prime\\=(A+B)(A^\prime B^\prime)=AA^\prime + AB^\prime + A^\prime B + BB^\prime=A^\prime B + AB^\prime=A \oplus B\)
逻辑函数的最简式
最简与或逻辑式
- 包含的与项最少;
- 每个与项的因子也已经最少。
例如:
\(Y = ABC+B^\prime C + ACD=ABC+B^\prime C=(AB+B^\prime)C=(A+B^\prime)C=AC+B^\prime C\)
\(Y=AC+B^\prime C + BD^\prime + CD^\prime + A(B+C^\prime)+A^\prime BCD^\prime + AB^\prime DE=AC+B^\prime C + BD^\prime + CD^\prime + A(B^\prime C)^\prime + AB^\prime DE\\ =AC+A+B^\prime C + BD^\prime +CD^\prime + AB^\prime DE=A+B^\prime C + BD^\prime + CD^\prime=A+B^\prime C + BD^\prime\)
逻辑函数的最小项之和标准形式
最小项
n变量逻辑函数的最小项m:m为与项、包含n个因子、每个变量都以原变量或反变量的形式在m中出现一次。
例如:两变量AB的最小项有:\(A^\prime B^\prime\),\(A^\prime B\),\(AB^\prime\),\(AB\),分别使他们函数值为1的取值组合为:00,01,10,11,因此这四个最小项的编号分别为\(m_0\),\(m_1\),\(m_2\),\(m_3\).
性质
- 任意输入变量取值,有且只有一个最小项的值为1
- 全体最小项之和为1
- 任意两个最小项之积为0
- 两个相邻的最小项(只有一个因子不同的最小项)之和可以合并,只留下公共因子:\(AB^\prime+AB=A\)
与或式->最小项之和
\(Y(A,B,C)=ABC^\prime + BC = ABC^\prime + BC(A+A^\prime)=ABC^\prime +ABC+A^\prime BC=\sum m(3,6,7)\)
最大项
n变量逻辑函数的最大项M:M为或项、包含n个因子、n个变量均以原变量或反变量的形式在M中出现一次。
例如:两变量AB的最小项有:\(A^\prime +B^\prime\),\(A^\prime +B\),\(A+B^\prime\),\(A+B\),分别使他们函数值为0的取值组合为:11,10,01,00,因此这四个最大项的编号分别为\(M_3\),\(M_2\),\(M_1\),\(M_0\).
性质
- 任意输入变量取值,有且只有一个最大项的值为0
- 全体最大项之积为0
- 任意两个最大项之和为1
- 两个相邻的最大项之积可以合并,只留下公共因子:\((A+B)(A+B^\prime)=AA+AB^\prime+AB+BB^\prime=A\)
或与式->最大项之积
\(Y(A,B,C)=(A+B+C^\prime)(B+C)=(A+B+C^\prime)(AA^\prime+B+C)\\=(A+B+C^\prime)(A+B+C)(A^\prime +B+C)=\prod_{i=0,1,4} M_i\).
最小项与最大项的关系
同一编号的\(m_i\)和\(M_i\)互为反函数。
最小项之和->最大项之积:\(Y=\sum m_i\),\(Y^\prime=(\sum m_i)^\prime=\sum_{k\neq i}m_k\),\(Y=(\sum_{k\neq i}m_k)^\prime = \prod_{k \neq i}m_k^\prime=\prod _{k\neq i}M_k\).
例如:\(Y=A^\prime BC^\prime + AB^\prime C + ABC^\prime +ABC=\sum_{i=2,5,6,7} m_i=\prod_{i=0,1,3,4}M_i\).
最大项之积变换为最小项之和也同理,例如:
\(Y=(A+B+C)(A+B+C^\prime)=\prod_{i=0,1}M_i = \sum_{i=2,3,4,5,6,7}m_i\)
卡诺图
卡诺图逻辑函数最小项之和的一种图形表示。
用\(2^n\)个小方格分别表示n变量所有最小项,卡诺图使得几何位置相邻的最小项在逻辑上也是相邻的。
注意,1.相邻的变量取值需要为格雷码;2.集合相邻包括上下左右相邻、上下环相邻、左右环相邻,对折位置重合相邻。
例如五变量的卡诺图可以是这样的:
从红线处折叠,那么\(m_9\)和\(m_{13}\)是重叠的,所以他们两个在逻辑上是相邻的。
对于卡诺图需要注意,如果让ABC成为列,DE成为行也是可以的,同理ABCD成为列,E成为行,无论如何变化方格的总数是不变的,都是\(2^5\)个。
卡诺图表示逻辑函数
方法1
- 将逻辑函数表示为最小项之和的形式;
- 在卡诺图上将这些最小项对应的方格填入1,其余方格填入0.
例如:\(Y=(ABC)=\sum_{i=5,6,7} AB^\prime C+ABC^\prime+ABC\),那么他的卡诺图为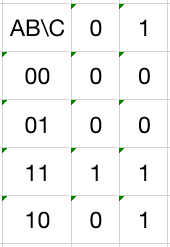
方法2
- 确定使每个与项为1的所有输出变量取值,行在卡诺图上对应方格填入1;
- 其余方格填入0.
例如:\(Y=C+AB^\prime\),那么只要\(C\)为1,\(Y\)的取值就是1;同理只要\(AB^\prime\)为1,\(Y\)的取值也是1。所以只需要在\(C\)为1的行或列填入1,在\(AB^\prime\)所在的行或列填入1即可。注意,卡诺图设计的时候应该将\(C\)放在一行,\(AB^\prime\)放在一行(大概?)

卡诺图化简逻辑函数
- 两个相邻的最小项可合并为一项,消去一个因子
- 四个相邻的最小项可合并为一项,消去两个因子
- 八个相邻的最小项可合并为一项,消去三个因子
例如:
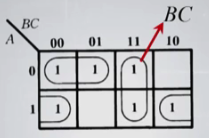
图中指向的两个最小项,他们的取值同时跨越了A=0和A=1,那么提取出BC后A就被消去,就只剩下BC,同理四个、八个。
卡诺图化简原则
- 要使化简之后与项的数量最少,应该让圈成的矩阵数量尽量少;
- 要使化简之后的与项因子最少,应该让圈成的矩阵尽量大;
- 圈中至少要有一个1只被当前的圈圈住,否则这个圈就是多余的
例如
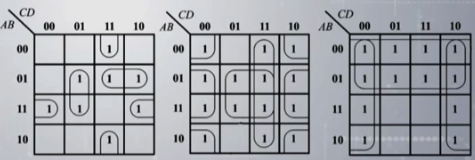
第一个化简之后的结果为:\(Y=BC^\prime D+B^\prime CD+A^\prime BC+ABD^\prime\).
第二个化简之后的结果为:\(Y=BD+CD+BD^\prime + B^\prime D^\prime\).
第三个化简之后的结果为:\(A^\prime + D^\prime\).
- \(Y=(A,B,C)=AC^\prime + A^\prime C + B^\prime C + BC^\prime\),他的卡诺图为:
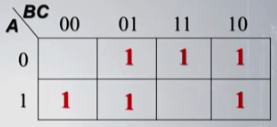
化简之后的结果为:\(Y=AB^\prime + A^\prime C + BC^\prime\),也可以为\(Y=B^\prime C+A^\prime B+AC^\prime\).
- \(Y=ABC+ABD+AC^\prime D+C^\prime D^\prime +AB^\prime C+A^\prime CD^\prime\),他的卡诺图为:
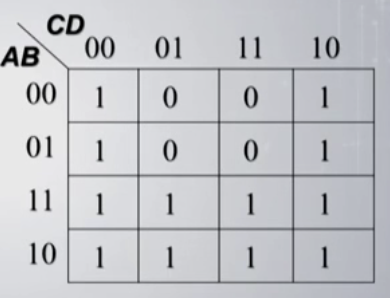
化简之后的结果为:\(Y=A+D^\prime\).
利用无关项化简逻辑函数
约束项和任意项
约束项:逻辑函数对输入变量的取值有限制,这些被限制的取值对应的最小项成为约束项。与约束项对应的输入取值组合不可能存在,因此约束项的取值总为0
任意项:在某些输入变量取值中,函数值为0或1不影响逻辑电路的功能,这些取值对应的最小项成为任意项
无关项:约束项和任意项统称为无关项,他们可以写入也可以不写入逻辑式
化简
- 加入无关项之后,应使化简后的项数最少,每项的因子最少
- 从几何上看,加入无关项之后应该让矩形圈最大、矩形数最少
例如
\(Y=A^\prime B^\prime C^\prime D+A^\prime BCD+AB^\prime C^\prime D^\prime\),给定的约束条件为\(A'B'CD+A'BC'D+ABC'D'+AB'C'D+ABCD+ABCD'+AB'CD'=0\),则函数的卡诺图为:
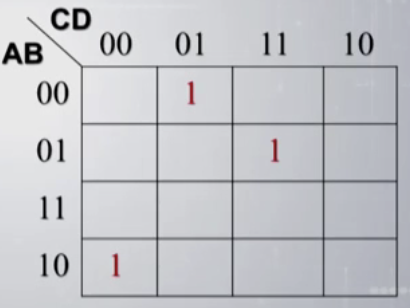
这样是无法构成2、4、8个相邻的最小项的,但是加入约束条件,在卡诺图中标出对应的最小项得到:
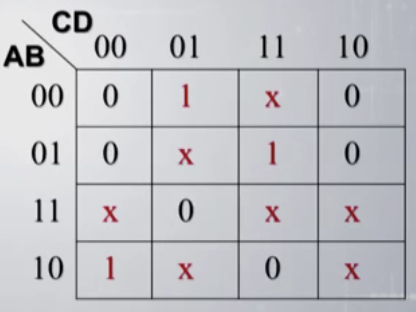
化简后可得到:\(Y=A'D+AD'=A\oplus D\).
\(Y(A,B,C,D)=\sum_{i=2,4,6,8}m_i\),约束条件为\(m_5+m_{10}+m_{11}+m_{12}+m_{12}+m_{14}+m_{15}=0\),则其卡诺图为:
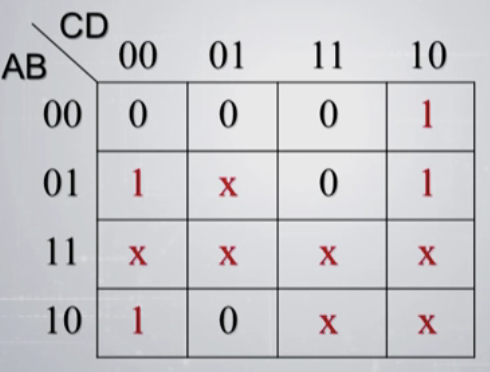
化简的结果为:\(Y=BC'+AD'+CD'\).



 浙公网安备 33010602011771号
浙公网安备 33010602011771号