图及最短路算法初步

图及最短路算法初步

什么是图？

图可以表示点与点之间的关系，它是由点集和边集构成。

生活中图的例子

高速公路连接全国各个城市，全国高速公路网可以简化成一个图模型：

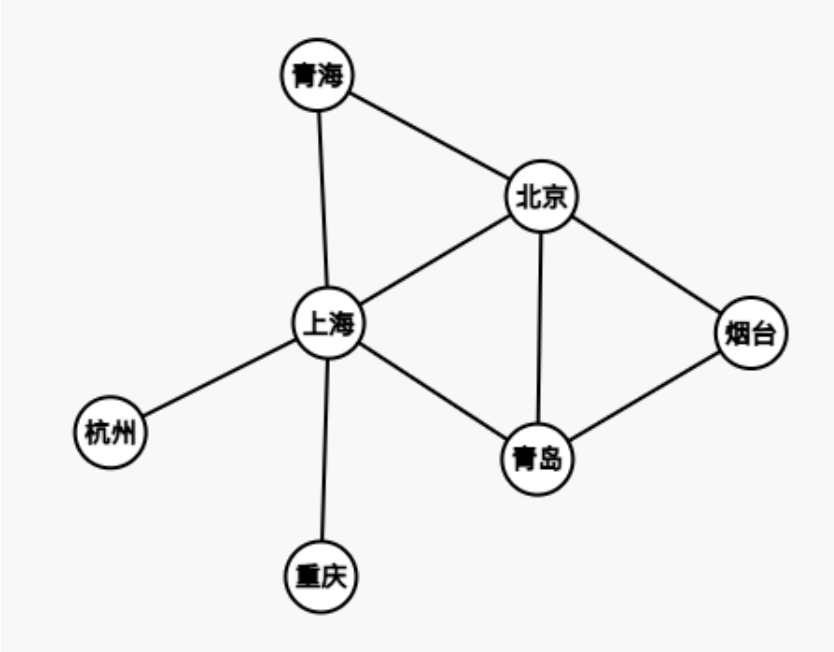
这就是一个图，它描述了两个城市之间是否有高速公路（边）.

图的一些基本概念

无向图：边没有方向的图称为无向图，刚刚简化之后的全国高速公路网就是一个无向图。

有向图：与无向图相反，边有方向的图成为有向图。

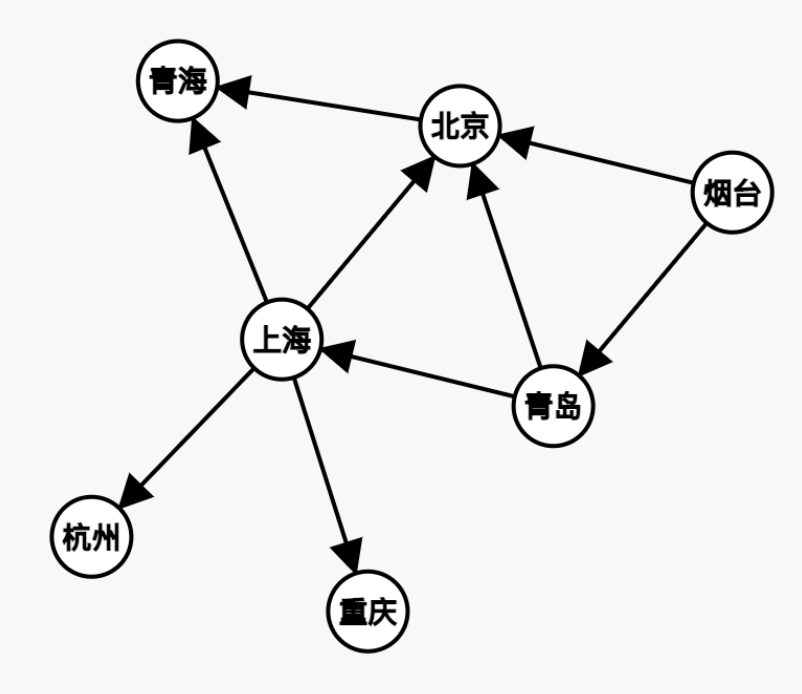
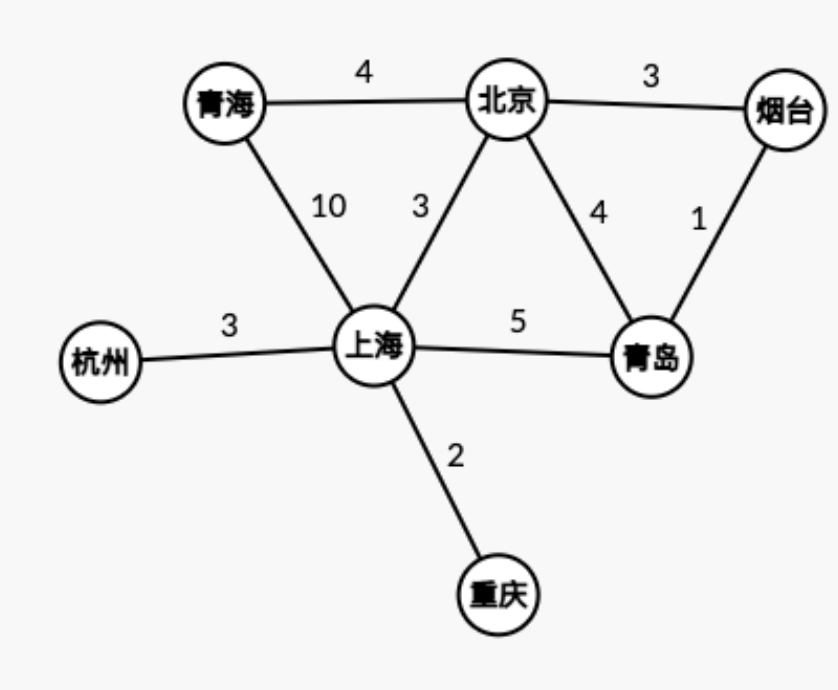
带权图：边有权值的图就是带权图，例如刚刚的图，描述从一个城市到另一个城市所需要的时间，那么边的权值就代表从边的一个点到另一个点所需要的时间。

无权图：边没有权值的图。

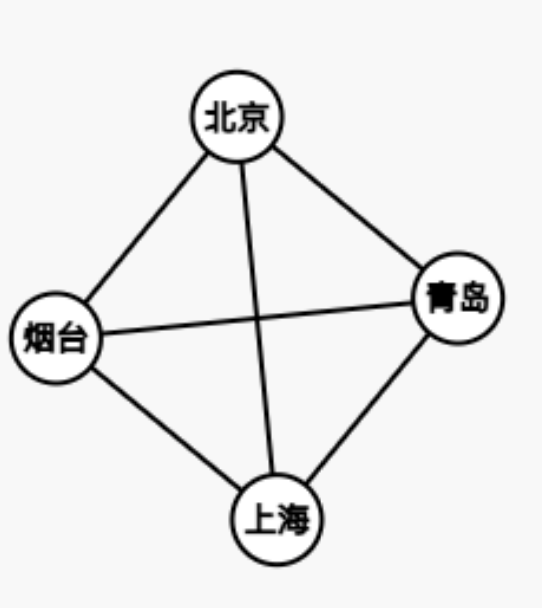
完全图：图中的任意一个点可以通过一个边到达任意一个其他点。

环：见图。

负环，又叫负权回路，负权环，指的是一个图中存在一个环，里面包含的边的边权总和<0。


图的存储

邻接矩阵

邻接矩阵是最简单的一种存储图的方式，它创建了一个二位数组e[Maxn][Maxn]，那么想要表示两个点\(u,v\)之间有一个边就表示为e[u][v] = e[v][u] = 1，这里1仅仅表示有边相连，如果这个边有边权\(w\)可以表示为：e[u][v] = e[v][u] = w.

此外邻接矩阵也可以表示有向图：若\(u,v\)之间只有从\(u\)指向\(v\)的边而没有从\(v\)指向\(u\)的边，那么e[u][v] = w即可。

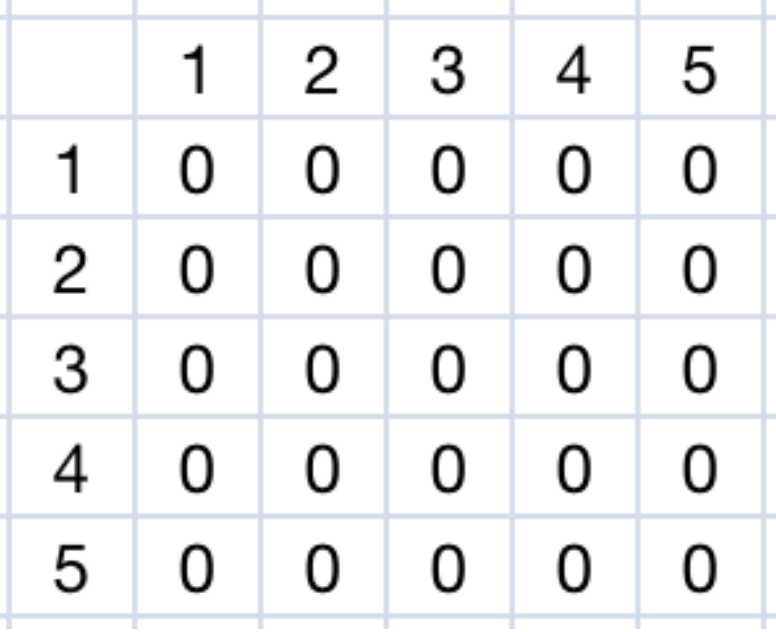
将有向边\((1,2)\)，\((1,5)\)，\((2,4)\)，\((3,1)\)，\((4,1)\)，\((5,2)\)添加到邻接矩阵中：

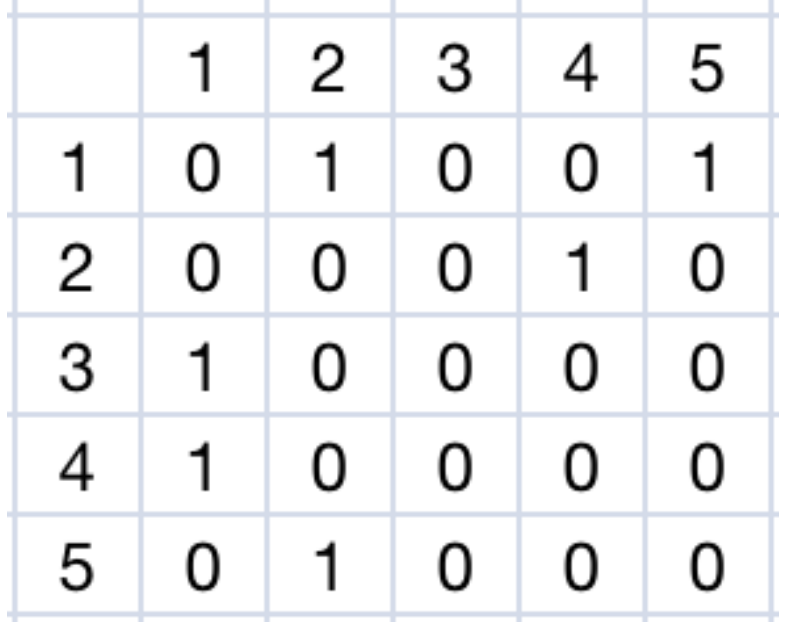
邻接表

用一个数组存储与一个点\(u\)相连的点有哪些。

将有向边\((1,2)\)，\((1,5)\)，\((2,4)\)，\((3,1)\)，\((4,1)\)，\((5,2)\)添加到邻接表中：

/* 使用之前清空ver和edge数组 */

const int MAX_EDGES = 100005;
vector<int> ver[MAX_EDGES], edge[MAX_EDGES];

void add(int u, int v, int w) {
    ver[u].push_back(v);
    edge[u].push_back(w);
}

/* 假设这里要找所有与u相连的点以及边的边权 */
void traverse(int u) {
  	for (int i = 0; i < ver[u].size(); i++) {
  	  int v = ver[u][i];
  		int w = edge[u][i];
		}
}

链式前向星

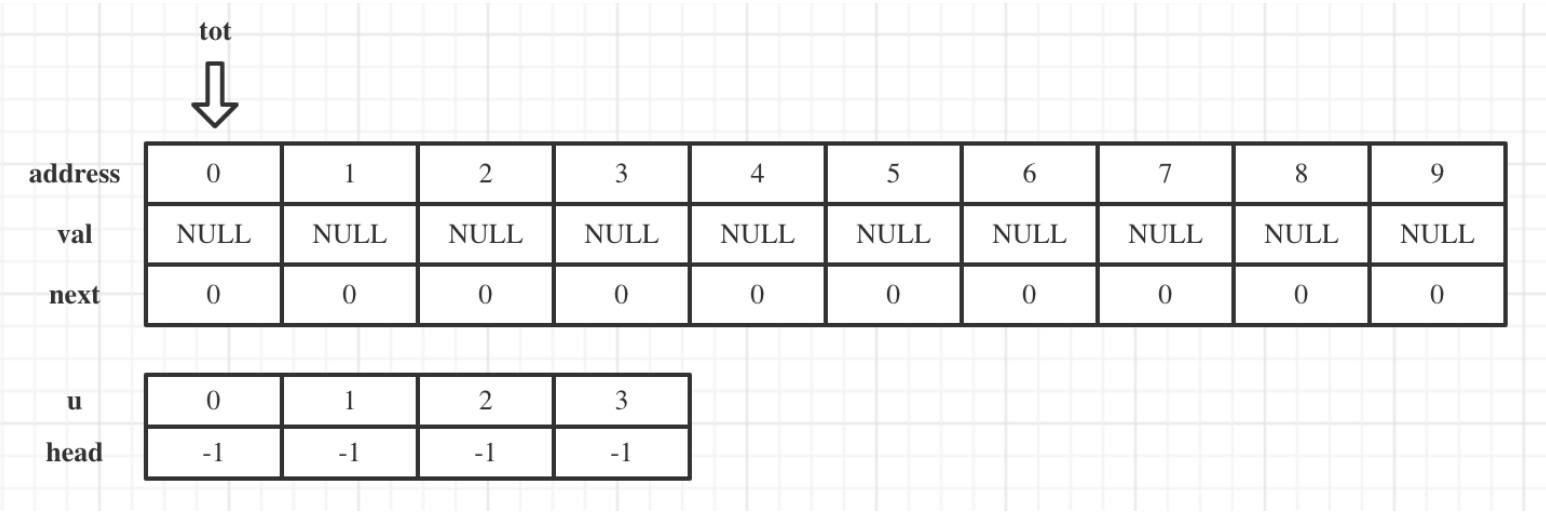
链表初步

有这样一个结构体数组：

struct Node {
  	int val, next;
} a[Maxn];

画成图：

那么这个开头地址为1的链表，表示的数字串就是：7,2,3,5,0,-2.

链式前向星

链式前向星的本质就是链表。

/* 使用之前调用init函数初始化 */

const int Maxn = 100005;
struct EDGE {
  	int v, w, next;
} e[Maxn << 1];

int head[Maxn], tot = 0;

void init() {
  	memset(head, -1, sizeof head);
  	tot = 0;
}

void add(int u, int v, int w) {
  	e[tot].v = v;
   	e[tot].w = w;
  	e[tot].next = head[u];
  	head[u] = tot++;
}

/* 假设这里要找所有与u相连的点以及边的边权 */
void traverse(int u) {
  	for (int i = head[u]; i != -1; i = e[i].next) {
      	int v = e[i].v;
      	int w = e[i].w;
    }
}

邻接表与链式前向星的优劣对比

在提前知道边数量的前提下，优先使用链式前向星，原因在于实现邻接表的\(vector\)的扩充机制会导致邻接表变慢。

* \(vector\)和数组在内存中都是连续的，不同的是\(vector\)的容量是可以变化的。假如一开始\(vector\)申请了一个长度为10的连续内存，那么当这些内存被用完之后，\(vector\)会再申请一个两倍于目前大小的内存，然后把原来内存中的内容复制到新申请的内存中，而这个复制的过程会比较慢。

最短路算法

什么是最短路？

最短路顾名思义，就是在一个图中找到两个点（vertex）之间的最短路径。这里的最短路径也不仅仅局限在距离的最短，也可以扩展到其他度量上，例如时间等。

常见的最短路算法

DFS（深度优先搜索）、BFS（广度优先搜索）

Dijkstra算法

Floyd算法

SPFA算法

DFS、BFS

DFS找到所有可能的路径取其中最短的一条作为最短路。

BFS个人认为在找最短路方面在各方面是比DFS优秀的，原因在于如果一个图是完全图，那么DFS是时间复杂度是\(O(n!)\)，大概有12个点DFS就会完全卡住，而BFS的时间复杂度是\(O(n)\)。

需要注意的是，DFS和BFS仅仅只能搜索边权值相等或者根本没有权的图，如果边的权值不相等，那么就需要用更高级的最短路算法进行最短路的寻找，比如下面就要讲到的Dijkstra算法。

Dijkstra算法

算法描述

Dijkstra算法采用了一种贪心的方法。

他用一个dis数组来存储从源点s到其他所有点的最短距离，这个dis的初始值全部设置为INF，可以用memset(dis, 0x3f, sizeof dis)\(^1\)来实现，而dis[s]初始化为0，原因显然，从s出发到s的最短路径就是0；

用一个集合来存储还没有求出最短路径的顶点，这里我们可以称这个集合为：我不知道我是不是“最短的”群体，简称U（unknown），在最一开始所有的顶点都在这个集合中，包括s；

用一个集合来存储已经求出来最短路径的顶点，我们称之为：我知道我是“最短的“群体，简称K（know），与U集合相反这个集合最一开始是空的。

以上就是开始求最短路开始之前的准备工作，下面介绍一下最短路的具体实现过程：

每次从“我不知道我是不是‘最短的’群体”（U）中找出dis最小的顶点（如果有多个选任意一个即可），假设这个点是\(V_{m}\)，

那么\(dis[V_{m}]\)从理论上来说就是从源点s到点\(V_{m}\)的最短路长度（对此有疑问的，下面会给出证明），

因为这个点已经能确定是最短路径，所以把它从“我不知道我是不是‘最短的’群体”集合中踢出去，把它加到“我知道我是’最短的‘群体”中，

同时把与\(V_m\)相连的顶点（\(V_{m_1},V_{m_2},..\)）进行“松弛”操作，什么是松弛操作呢？

就是看看从源点s途径\(V_m\)（最短路）到达与\(V_m\)相连的顶点（\(V_{m_i}\)）的距离会不会比原来的\(dis[V_{m_i}]\)要小，如果是那么就更新把\(dis[V_{m_i}]\)更新一下。

简单来说就是一行代码dis[v] = dis[u] + w，其中v是上面提到的\(V_{m_i}\)，u是上面提到的\(V_m\)，w是u、v之间边的权值。

重复上面操作直到集合“我不知道我是不是’最短的‘群体”变成空的（或者“我知道我是’最短的‘群体”包含图中全部的点），算法就结束了，\(dis\)数组中存储的就是最终最短路的结果。

总结一下就是说，从集合U中找到\(dis\)最小的顶点，把它加入到集合K中，从集合U中去除掉，并对与该点相连的点进行松弛操作。

伪代码

set U, K;
把所有的顶点加到集合U中;
dis[nv];
memset(dis, 0x3f, sizeof dis);
while U is not empty:
	minn = INF;
	u = -1;
	for each vertex v in U:
		if dis[v] <= minn:
			minn = dis[v];
			minn_vertex = v;
	U.erase(u);
	K.insert(u);
	for each v connect to u:
		if dis[v] > dis[u] + w:
			dis[v] = dis[u] + w;

算法演示

以下面这张图作为演示，源点s设为0.

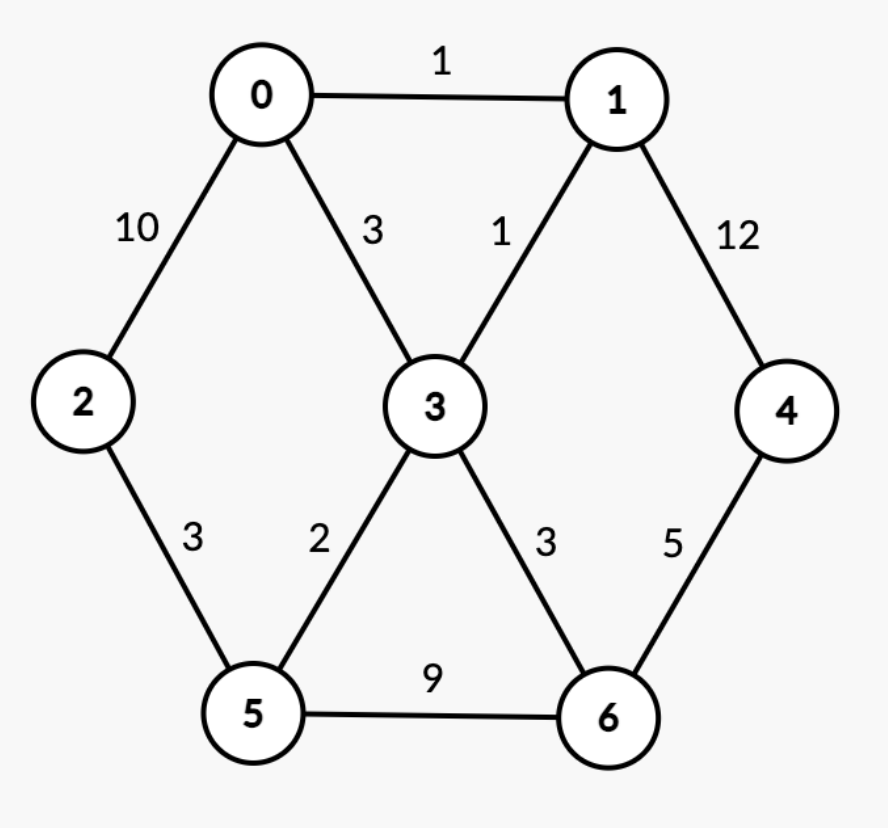
初始状态下\(dis\)、\(U\)、\(K\)的情况如下：

vertex	0	1	2	3	4	5	6
dis	0	INF	INF	INF	INF	INF	INF

U	K
0、1、2、3、4、5、6	NULL

1. 从集合U中找\(dis\)最小的顶点，得到顶点0；

   把0加入到集合K，从集合U中去除掉，对0周围的顶点进行松弛，现在的状态如下：

   vertex	0	1	2	3	4	5	6
   dis	0	1	10	3	INF	INF	INF

U	K
1、2、3、4、5、6	0

2. 从集合U中找\(dis\)最小的顶点，得到顶点1；

把1加入到集合K，从集合U中去除掉，对1周围的顶点进行松弛，现在的状态如下：

vertex	0	1	2	3	4	5	6
dis	0	1	10	2	13	INF	INF

U	K
2、3、4、5、6	0、1

3. 从集合U中找\(dis\)最小的顶点，得到顶点3；

把3加入到集合K，从集合U中去除掉，对3周围的顶点进行松弛，现在的状态如下：

vertex	0	1	2	3	4	5	6
dis	0	1	10	2	13	4	5

U	K
2、4、5、6	0、1、3

4. 从集合U中找\(dis\)最小的顶点，得到顶点5；

把5加入到集合K，从集合U中去除掉，对5周围的顶点进行松弛，现在的状态如下：

vertex	0	1	2	3	4	5	6
dis	0	1	7	2	13	4	5

U	K
2、4、6	0、1、3、5

4. 从集合U中找\(dis\)最小的顶点，得到顶点6；

把6加入到集合K，从集合U中去除掉，对6周围的顶点进行松弛，现在的状态如下：

vertex	0	1	2	3	4	5	6
dis	0	1	7	2	10	4	5

U	K
2、4	0、1、3、5、6

5.6. 从集合U中得到2和4，重复上面点操作。

算法结束后dis数组情况如下：

vertex	0	1	2	3	4	5	6
dis	0	1	7	2	10	4	5

小注：上面提到的集合k没有实际在下面的代码中并没有体现，而之所以提到它是因为这个算法的标准描述中提到了这样一个集合。

对算法进行优化

优先队列初步

优先队列的使用

优先队列\(priority\_queue\)在头文件\(queue\)中。

它是与队列\(queue\)相似，\(queue\)每次是将最先进入队列的元素弹出队列，而\(priority\_queue\)是将优先级最高的元素弹出队列。

在\(priority\_queue\)中，元素的优先级是由运算符\(<\)决定的，举两个例子：

​ 1. 在优先队列中有四个整数\(1,4,6,11\)，他们的关系是\(1<4<6<11\)，所以在这个优先队列中，弹出队列的顺序依次是\(11,6,4,1\)；

2. 在优先队列中有四个整数$1,4,6,11$，首先先弹出来一个元素，再在优先队列中插入三个元素：$3,12,5$，之后再不断的从队列中弹出元素直到为空，那么弹出的顺序就是：$11，12，6，5，4，3，1$.

优先队列的基本操作：

\(push\) 向队列中插入一个元素

\(top\) 与队列\(queue\)的\(front\)类似，前者是从优先队列中弹出优先级最高的元素，后者是从队列中弹出最先进入队列的元素。

\(empty\) 如果优先队列为中返回\(true\)否则返回\(false\).

时间复杂度：

优先队列使用堆实现的，\(top\)操作复杂度为\(O(1)\)，\(push\)操作的复杂度\(O(logn)\).

结构体运算符重载

在内建类型中比如\(int,double\)，他们可以进行\(+-*/ \le \ge\)等操作，但是在自己定义一个结构体，比如下面这个结构体：

struct Node {
  int a, b;
};

在重载结构体运算符之前，两个\(Node\)相加的意思可能是\(a,b\)分别相加得到新的 \(Node\)也可能是两个\(Node\)的\(a\)分别相加，两个\(b\)取较大的一个得到新的\(Node\)，甚至可以是其他的操作。

在这些操作中可能你自己比较清楚究竟你的\(+\)想要完成什么操作，但是计算机是不清楚的，所以需要明确的告诉计算机\(+\)究竟是要完成怎样的操作。

而告诉计算机的方式就是重载运算符。

比如想要对结构体重载\(+\)运算符，完成的操作是上面提到的第二种“两个\(Node\)的\(a\)分别相加，两个\(b\)取较大的一个得到新的\(Node\)”：

struct Node {
  int a, b;
  bool operator + (const Node &x) const {
    Node res;
    res.a = a + x.a;
    res.b = std::max(b, x.b);
  }
};

重载\(<\)运算符,完成的操作是比较两个\(Node\)的\(a+b\)的大小：

struct Node {
  int a, b;
  bool operator + (const Node &x) const {
    Node res;
    res.a = a + x.a;
    res.b = std::max(b, x.b);
  }
  bool operator < (const Node &x) const {
    return a + b < x.a + x.b;
  }
};

需要注意的是只有运算符才能重载，比如+-*/^&|，而不能重载一个字母或者一个不是运算符的符号。

对于其他的运算符可以参照上面的代码自行修改。

结构体初始化函数

参照前面说到的结构体\(Node\)，创建\(Node\)的对象：

struct Node {
  int a, b;
}x, y[100];
Node c[100], d[100]; 
// 这里演示创建结构体对象的方法，这段代码中x,y,c,d都是有效的。

现在要对\(x\)进行赋值，可以这样写：

x.a = 1; x.b = 2;

也可以定义一个结构体初始化函数：

struct Node {
  int a, b;
  Node(){}
  Node(int a, int b):a(a), b(b){}
}x;

这样对\(x\)进行赋值就可以这样写：

x = Node(1, 2);

注意到在定义初始化函数的时候，有这样的一句Node(){}，它是用来重载的，如果没有这个语句在声明对象的时候会出现问题，有兴趣的自行查阅资料，这里不展开。

优先队列对算法进行优化

思考

观察上面提到的Dijkstra伪代码：

set U;
把所有的顶点加到集合U中;
dis[nv];
memset(dis, 0x3f, sizeof dis);
while U is not empty:
	minn = INF;
	u = -1;
	for each vertex v in U:
		if dis[v] <= minn:
			minn = dis[v];
			minn_vertex = v;
	U.erase(u);
	for each v connect to u:
		if dis[v] > dis[u] + w:
			dis[v] = dis[u] + w;

如果这段程序真正运行起来的时候，上面的哪一步操作会消耗大量的时间？

“寻找集合U中\(dis\)最小的顶点”这个操作会消耗大量的时间，因为每次查找都要把U集合完整遍历一遍才能知道哪个点的\(dis\)是最小的，查找复杂度是\(O(n)\)，当nv比较大的时候很容易就TLE，因此需要对它进行优化。

首先，想一下\(dis\)最小的点可能会出现在哪里？

\(dis\)最小的点一定是已经是在经过松弛操作之后后的点中出现，因为没有经过松弛操作的点的\(dis\)是无穷大，只要经过松弛操作的点就一定比无穷大要小。

其次，在有了上面结论之后，优先队列是够能辅助完成“寻找集合U中\(dis\)最小的顶点”这个操作？

优先队列\(push\)和\(top\)这两个操作都非常的快，我们定义一个结构体，里面包含点和\(dis\)这两个信息，并对\(<\)运算符进行重载，使得\(dis\)小的元素优先出队。这样在每次松弛操作之后，就将被松弛的点以及\(dis\)打包进结构体并\(push\)进优先队列。这样每次只用\(O(logn)\)的时间就能找到\(dis\)最小的点，相比之前的\(O(n)\)可以说是巨幅优化。

Dijkstra算法模版题

题目：

给定一个\(n\)个点，\(m\)条有向边的带非负权图，请你计算从\(s\)出发，到每个点的最短距离。

数据不保证你能从\(s\)出发到任意点，如果不能到达输出\(-1\)。

提示：

不能到达的点\(dis\)是INF.

代码：

见附录A-1

算法正确性证明

为什么要进行正确性证明

算法证明

Dijkstra算法的变形-最长边最短的路径

题目：

给定一个\(n\)个点，\(m\)条有向边的带非负权图，请你计算从\(s\)出发，到每个点的路径中最长的边最短是多少？

松弛代码：

if (dis[v] > std::min(dis[u], w)) dis[v] = std::min(dis[u], w)

完整代码：

见附录A-2

Dijkstra算法的变形-最短边最长的路径

题目：

给定一个\(n\)个点，\(m\)条有向边的带非负权图，请你计算从\(s\)出发，到每个点的路径中最短的边最长是多少？

松弛代码：

if (dis[v] < std::max(dis[u], w)) dis[v] = std::min(dis[u], w)

完整代码：

见附录A-3

Dijkstra算法的一个小技巧-反向建边

完整代码：

见附录A-4

时间复杂度和空间复杂度分析

小结

核心是松弛

Floyd算法

算法描述

伪代码（和真的一样）

时间复杂度和空间复杂度（需要注意的问题）

算法正确性（略）

Floyd算法模版题

Floyd算法的变形-

Cow Contest

Floyd算法的变形-

灾后重建

Floyd判断负环

SPFA算法

算法描述

伪代码

算法正确性证明（略）

时间复杂度和空间复杂度

SPFA模版题

单源最短路径（弱化版）

什么是负环

用SPFA进行负环判断

负环

总结

加餐（我当时的一些疑问）

memset赋初始值

结构体重载运算符

结构体的初始化函数

优先队列的一些基本使用

为什么优先队列比较为false的优先出队列？

路径记录

附录A-代码

1. Dijkstra算法模版题

#include <cstdio>
#include <cstring>
#include <queue>

const int Maxn = 500005;
const int INF = 0x3f3f3f3f;

struct EDGE {
    int v, w, next;
} e[Maxn << 1];

int head[Maxn], tot = 0;

void add(int u, int v, int w) {
    e[tot].v = v;
    e[tot].w = w;
    e[tot].next = head[u];
    head[u] = tot++;
}

struct Node {
    int pos, dis;
    Node(){}
    Node(int pos, int dis):pos(pos), dis(dis){}
    bool operator < (const Node &x) const {
        return dis > x.dis;
    }
};

int dis[Maxn];
bool vis[Maxn];

void dijkstra(int s) {
    memset(vis, 0, sizeof vis);
    memset(dis, INF, sizeof dis);
    dis[s] = 0;
    std::priority_queue<Node>q;
    q.push(Node(s, 0));
    for (; !q.empty();) {
        Node f = q.top();
        q.pop();
        int u = f.pos;
      	if (vis[u]) continue;
      	vis[u] = true;
        for (int i = head[u]; i != -1; i = e[i].next) {
            int v = e[i].v;
            int w = e[i].w;
            if (dis[v] > dis[u] + w) {
                dis[v] = dis[u] + w;
                q.push(Node(v, dis[v]));
            }
        }
    }
}

void solve() {
    memset(head, -1, sizeof head);
    int nv, ne, s;
    scanf("%d %d %d", &nv, &ne, &s);
    int u, v, w;
    for (int i = 0; i < ne; i++) {
        scanf("%d %d %d", &u, &v, &w);
        add(u, v, w);
    }
    dijkstra(s);
    for (int i = 1; i <= nv; i++) {
        printf("%d%c", dis[i] == INF ? -1 : dis[i], " \n"[i == nv]);
    }
}

int main() {
    solve();
    return 0;
}

2. Dijkstra算法的变形-最长边最短的路径

3. Dijkstra算法的变形-最短边最长的路径

4. Dijkstra算法的一个小技巧-反向建边

附录B-证明

参考文献

[1] 最短路径 | 深入浅出Dijkstra算法（一）

[2] 最短路径问题---Dijkstra算法详解

[3] 百度百科-迪克斯特拉算法

[4] c++图论vector邻接表与链式前向星性能差异

[5] 优先队列用法

[6] 图论入门及基础概念（图篇）

[7] 负环

[8] 邻接表模板（算法竞赛进阶指南）

[9] 通俗易懂讲解 链表