UVA-514 Rails

UVA-514 Rails

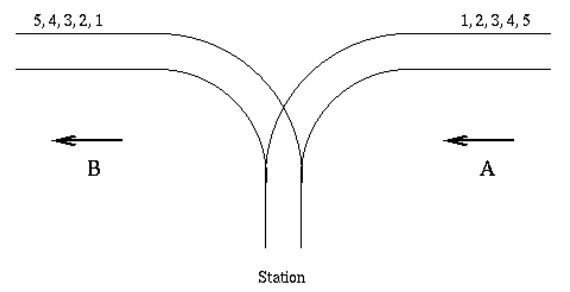
题意：

如图有一个铁路中转站，在A侧有\(n\)个车厢，从左到右编号分别为\(1,2,3..,n\)，现在你可以通过中间的中转站(\(station\))对这些车厢进行重新排序。给出你重新排序之后的车厢编号问你是否合法。

需要注意的是，假如一个车厢从\(A\)进入了中转站，那么它只能从中转站进入到\(B\)而不能返回\(A\)。进入到\(B\)之后的车厢只能留在\(B\)，不能返回中转站或者\(A\)。

---

思路：

铁路中转站相当于一个栈。

从前到后在\(A\)中找\(B\)的数字。具体方法为如果\(A\)当前的数字与\(B\)当前的数字相等那么直接\(A++,B++\)，如果不相等就检查一下栈顶是否与\(B\)当前数字相等，如果还是不相等，那么如果\(A\)还可以进栈（即\(A<n\)），那么就让\(A\)进栈。如果上述操作都不能进行了那么这个序列\(B\)就是非法的。

---

参考代码：

代码目前仅通过样例，正确性有待商榷，OJ最近进不去没法评测。

#include <cstdio>
#include <iostream>
#include <stack>

const int Maxn = 1005;

int a[Maxn];

void solve(int n) {
	for (int i = 1; i <= n; i++) {
		scanf("%d", a + i);
	}
	std::stack<int>s;
	int A = 1, B = 1;
	bool flag = true;
	while (B <= n) {
		if (A == a[B]) {
			A++;
			B++;
		} else if (!s.empty() && s.top() == a[B]) {
			s.pop();
			B++;
		} else if (A < n) {
			s.push(A++);
		} else {
			flag = false;
			break;
		}
	}
	printf("%s\n", flag ? "Yes" : "No");
}

int main() {
	int n;
	while (~scanf("%d", &n) && n) {
		solve(n);
	}
	return 0;
}