图解排序算法,这五种最热门!
文章首发于公众号「陈树义」及个人博客 shuyi.tech,欢迎关注访问。
说到排序算法,大家估计都比较熟悉,但要你一下子写出来又蒙圈了。所以这篇文章不会讲解所有的排序算法,而是挑选最热门的五种:冒泡排序、选择排序、插入排序、快速排序、归并排序。
我们通过图文 + 流程解释 的方式,让大家能快速领悟到各个排序算法的思想,从而达到快速掌握的目的。此外每个排序算法都有对应的 Github 代码实现,可供大家调试理解算法。同时也附上了文章中所画图的 draw.io 数据文件,方便大家根据自己的习惯进行修改。
排序算法的仓库地址:java-code-chip/src/main/java/tech/shuyi/javacodechip/sort at master · chenyurong/java-code-chip
如果你已经不是第一次学习排序算法,那么我建议你按照这样的思路学习:
- 通过图解或调试,弄清楚每个算法的思想。
- 下载 Github 例子,尝试自己手写实现。
- 定期复习手写实现,不断巩固知识点。
好了,废话不多说,让我们开始今天的图解排序算法吧!
选择排序
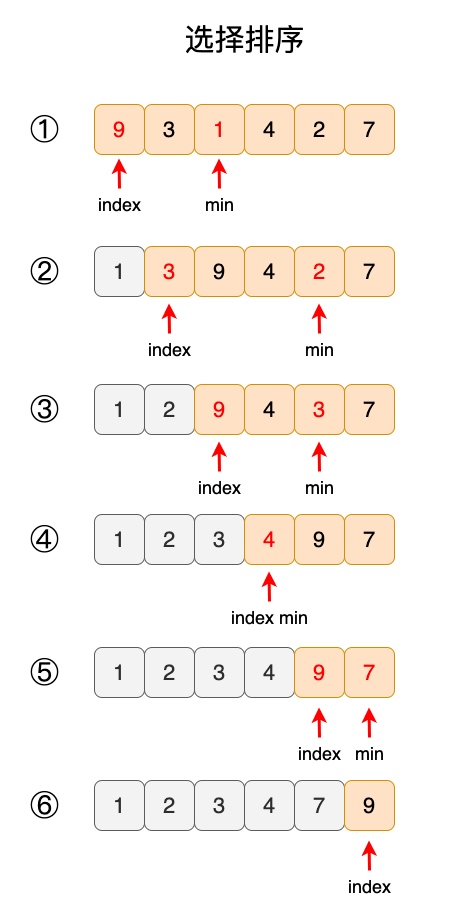
选择排序,意思是每次从待排序的元素选出极值作为首元素,直到所有元素排完为止。 其详细的排序逻辑如下图所示:
- 第 1 次,index 下标对应值为 9,找出所有最小值为 1,将 9 与 1 交换位置,得到 ②。同时,index 下标加一。
- 第 2 次,index 下标对应值为 3,找出所有最小值为 3,将 3 与 2 交换位置,得到 ③。同时,index 下标加一。
- 第 3 次,index 下标对应值为 9,找出所有最小值为 3,将 9 与 3 交换位置,得到 ④。同时,index 下标加一。
- 一直这样循环下去,直到 index 下标到达数组边界,如 ⑥ 所示。
注意:灰色部分表示已经完成排序的部分。
选择排序的算法比较简单,如下所示:
public static void selectSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
int min = i;//每一趟循环比较时,min用于存放较小元素的数组下标,这样当前批次比较完毕最终存放的就是此趟内最小的元素的下标,避免每次遇到较小元素都要进行交换。
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) {
min = j;
}
}
//进行交换,如果min发生变化,则进行交换
if (min != i) {
swap(arr,min,i);
}
}
}
可调式代码地址:java-code-chip/SelectSort.java at master · chenyurong/java-code-chip
简单选择排序通过上面优化之后,无论数组原始排列如何,比较次数是不变的;对于交换操作,在最好情况下也就是数组完全有序的时候,无需任何交换移动,在最差情况下,也就是数组倒序的时候,交换次数为n-1次。综合下来,时间复杂度为O(n2)。
冒泡排序
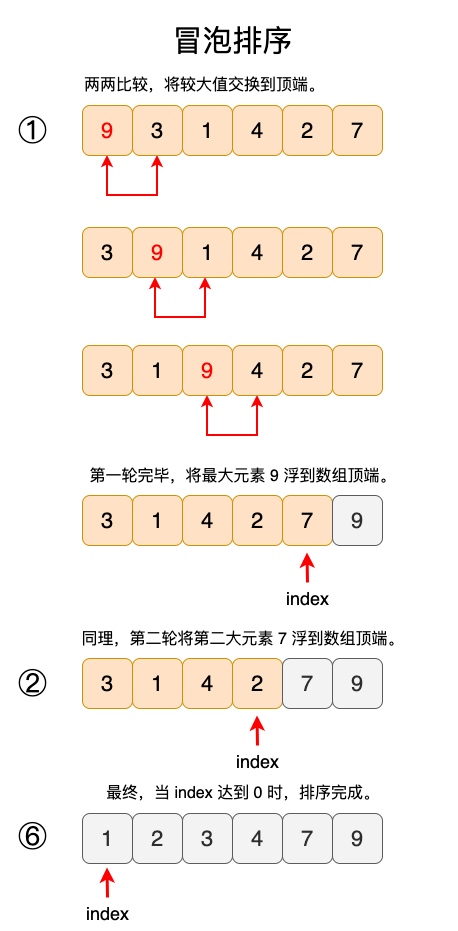
冒泡排序,就是像池塘里的水泡一样往上冒泡。我们可以理解成一个数不断地往上冒泡(比较交换),一直到最上面(末尾)。通过不断往上冒泡,每次冒泡都会将最值浮到最上层,最终达到完全有序。 其详细的排序算法逻辑如下:
- 第 1 轮,9 大于 3,那么将 9 与 3 交换,接着继续往下比较。9 大于 1,那么将 9 与 1 交换,接着往下比较,最终我们将 9 浮到数组顶端。此时 index 指向数组顶端,该数是有序的了,因此 index 减一。
- 第 2 轮,3 大于 1,那么 3 与 1 交换,接着往下比较。最终,我们只需要比较到 index 位置即可,最终我们将 7 浮到数组顶端。同时 index 也减一,此时 7、9 是有序的。
- 如此这样反复循环,直到 index 下标达到 0 即可。
在冒泡排序的过程中,如果某一趟执行完毕,没有做任何一次交换操作,那么就说明剩下的序列已经是有序的了。例如数组[5,4,1,2,3],执行了两次冒泡之后,其数组变为 [1,2,3,4,5]。此时,index 下标指向 3 这个值。再执行第三次冒泡时,我们会发现 1<2<3,我们一次交换都没有做,这就说明剩下的序列已经是有序的,排序操作已经完成,不需要再进行排序了。
public static void bubbleSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
boolean flag = true;//设定一个标记,若为true,则表示此次循环没有进行交换,也就是待排序列已经有序,排序已然完成。
for (int j = 0; j < arr.length - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr,j,j+1);
flag = false;
}
}
if (flag) {
break;
}
}
}
可调试代码地址:java-code-chip/BubbleSort.java at master · chenyurong/java-code-chip
插入排序
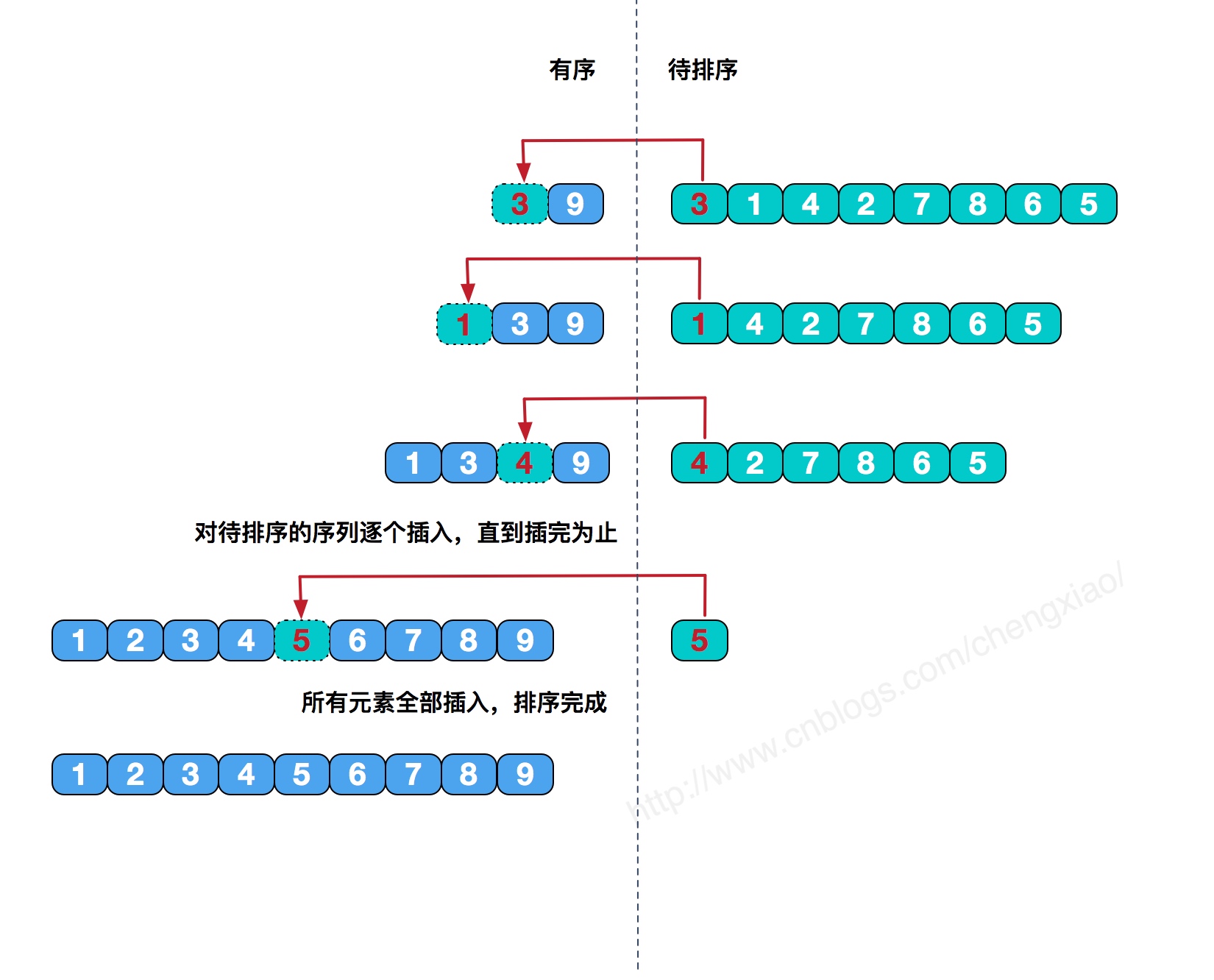
插入排序,即将元素一个个插入新的数组系列中,直到所有元素插完为止。 例如下图的例子,第 1 次将元素 9 插入新的数组中
/**
* 插入排序
*
* @param arr
*/
public static void insertSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
int j = i;
while (j > 0 && arr[j - 1] > arr[j]) {
swap(arr,j,j-1);
j--;
}
}
}
可调式代码地址:java-code-chip/InsertSort.java at master · chenyurong/java-code-chip
简单插入排序在最好情况下,需要比较n-1次,无需交换元素,时间复杂度为O(n);在最坏情况下,时间复杂度依然为O(n2)。但是在数组元素随机排列的情况下,插入排序还是要优于上面两种排序的。
快速排序
快速排序,顾名思义其排序效率非常高,所以才叫快速排序。快速排序的核心思想是选取一个基准数,通过一趟排序将小于此基准数的数字放到左边,将大于此基准数的数字放到右边。之后再用遍历不断地对左右子串进行同样的操作,从而达到排序的目的。 快速排序的时间复杂度在最坏情况下是 O(N2),平均的时间复杂度是 O(N*lgN)。
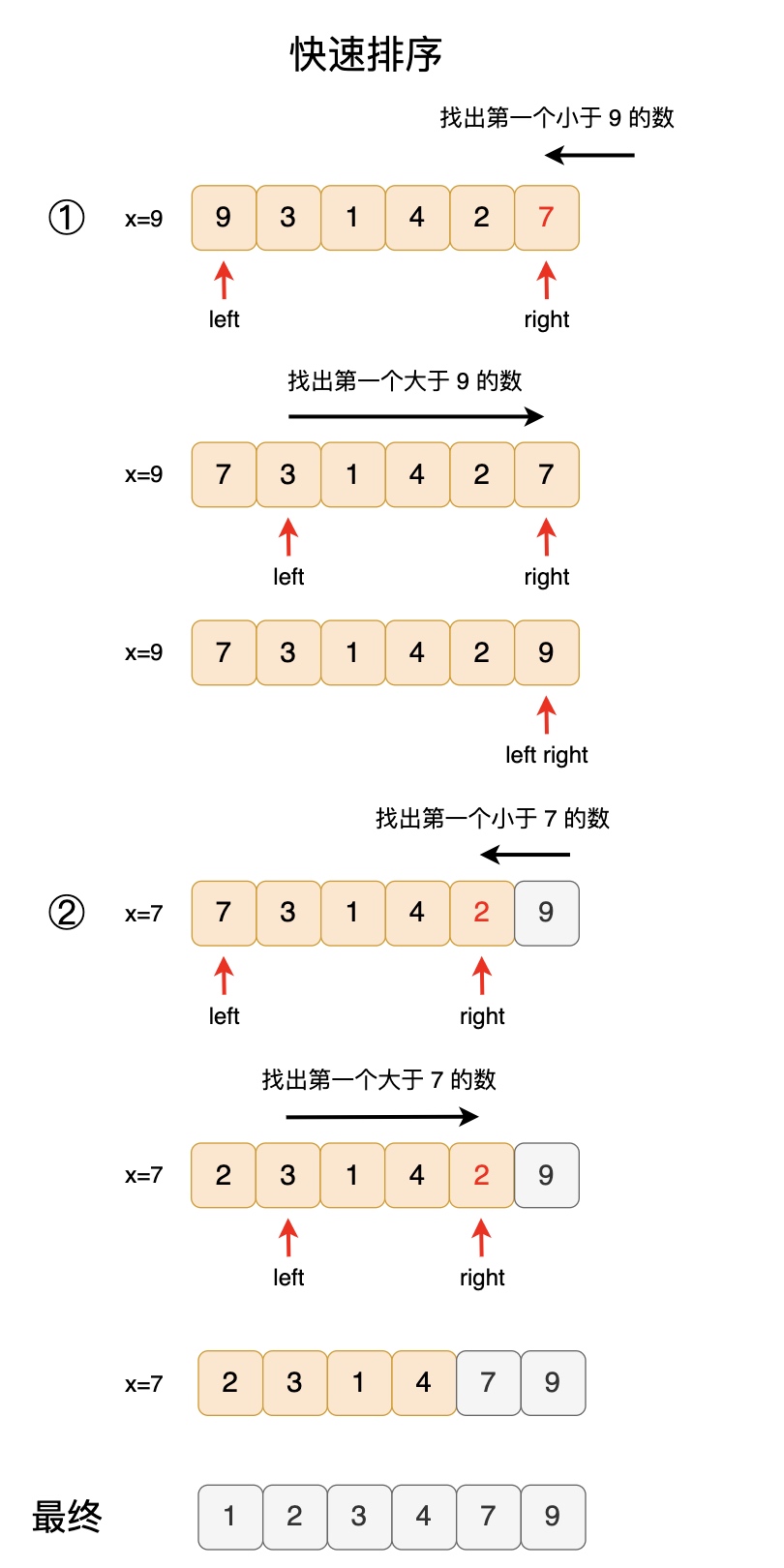
例如下图中的例子,在第一趟排序里,我们选中了基准数为 9,那么此次排序就把所有比 9 小的数放到了左边,所有比 9 大的数放到了右边。在第二趟排序里,我们选中了基准数为 7,那么此次排序就把所有比 7 小的数放到了左边,所有比 7 大的数放到了右边。
我们以对 9 3 1 4 2 7 整数串进行排序为例,详细讲解整个快速排序的流程:
- 选取 9 为基准数,从 right 开始,从右到左找出第一个小于 9 的数。
- 第一个数是 7,小于 9,符合条件。于是将找到的这个数值放到 left 位置上,同时 left 加一。
- 从 left 开始,从左到右选取第一个大于 9 的数。
- 可以看到子串中并没有一个大于 9 的数,于是 left 会一直累加到 right 的位置。
- 当 left >= right 时,单趟排序结束,将基准数填入 left 所在位置。
- 最终整个字符串被以 9 为基准数,切割成两部分,左边部分比 9 小,右边部分比 9 大。
接着进行第二次排序,第二次排序的整体流程如下:
- 选取 7 为基准数,从 right 开始,从右到左找出第一个小于 9 的数。
- 第一个数是 2,小于 9,符合条件。于是将找到的这个数值放到 left 位置上,同时 left 加一,此时数组变为:2 3 1 4 2 9。
- 从 left 开始,从左到右选取第一个大于 9 的数。
- 可以看到子串中并没有一个大于 9 的数,于是 left 会一直累加到 right 的位置。
- 当 left >= right 时,单趟排序结束,将基准数填入 left 所在位置。
- 最终整个字符串被以 7 为基准数,切割成两部分,左边部分比 7 小,右边部分比 7 大。
剩余的子串都进行同样的处理逻辑,最终我们可以得到一个排序的整数串。
代码实现:
/**
* v
* @param arr -- 待排序的数组
* @param l -- 数组的左边界(例如,从起始位置开始排序,则l=0)
* @param r -- 数组的右边界(例如,排序截至到数组末尾,则r=arr.length-1)
*/
public static void quickSort(int arr[], int l, int r) {
if (l < r) {
int i,j,x;
i = l;
j = r;
x = arr[i];
while (i < j)
{
// 从右向左找第一个小于x的数
while(i < j && arr[j] > x) {
j--;
}
if(i < j) {
arr[i] = arr[j];
i++;
}
// 从左向右找第一个大于x的数
while(i < j && arr[i] < x) {
i++;
}
if(i < j) {
arr[j] = arr[i];
j--;
}
}
arr[i] = x;
quickSort(arr, l, i-1);
quickSort(arr, i+1, r);
}
}
可调式代码地址:java-code-chip/QuickSort.java at master · chenyurong/java-code-chip
归并排序
归并排序,其英文名为 Merge Sort,其意思是将排序串拆分成最小的单位之后,再一个个合并成有序的子串。 例如下图的整数串,将其拆分成最小的子串就是每个只有一个整数。之后再将每个单个的子串合并起来,例如:8 与 4 合并起来成为有序子串 4、8,5 与 7 合并起来成为有序子串 5、7。4、8 和 5、7 再合并成为有序子串 4、5、7、8。
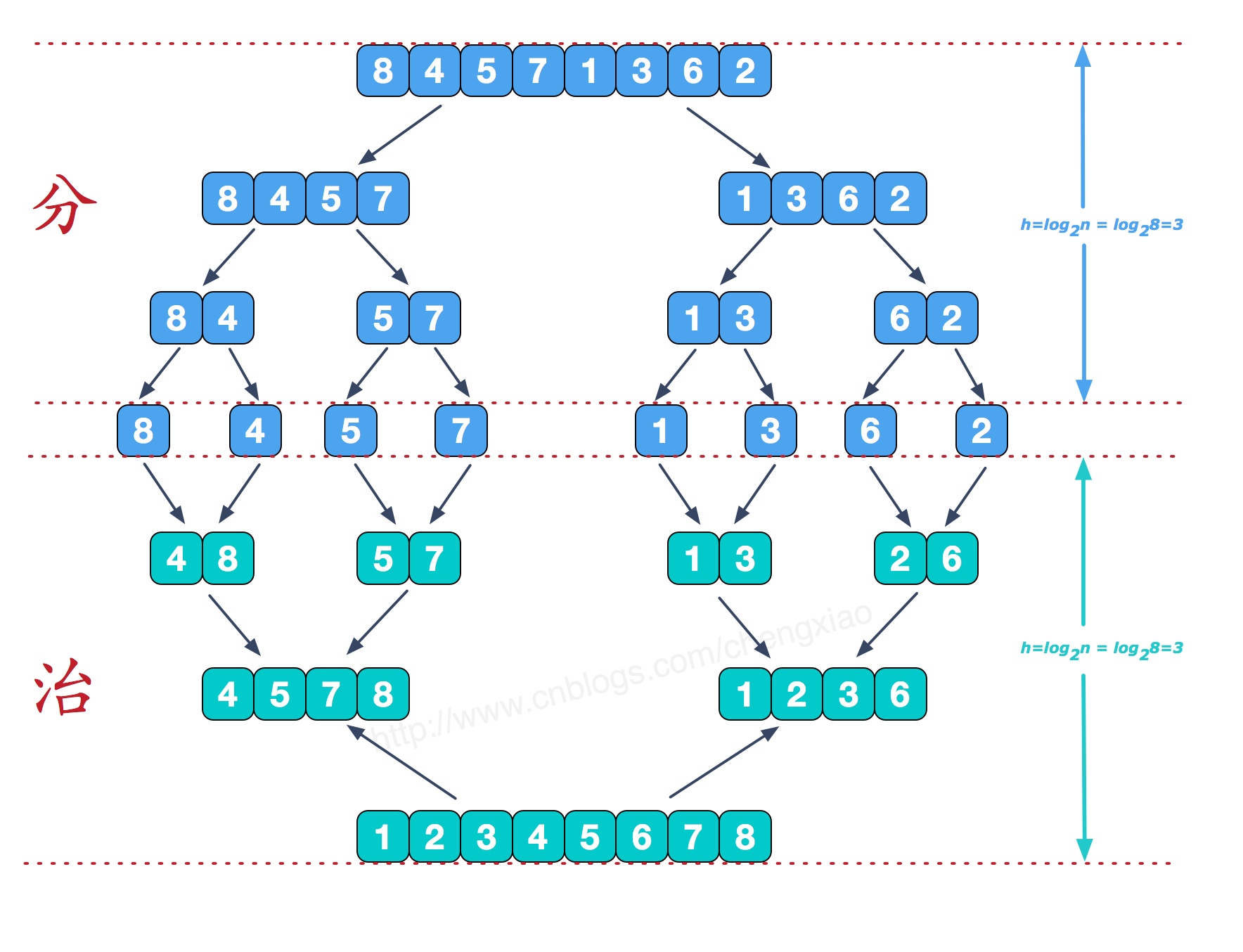
可以看到在这个过程中,最关键是合并两个有序子串的算法。这里我们以 [4,5,7,8] 和 [1,2,3,6] 为例,讲解有序子串合并的算法流程。
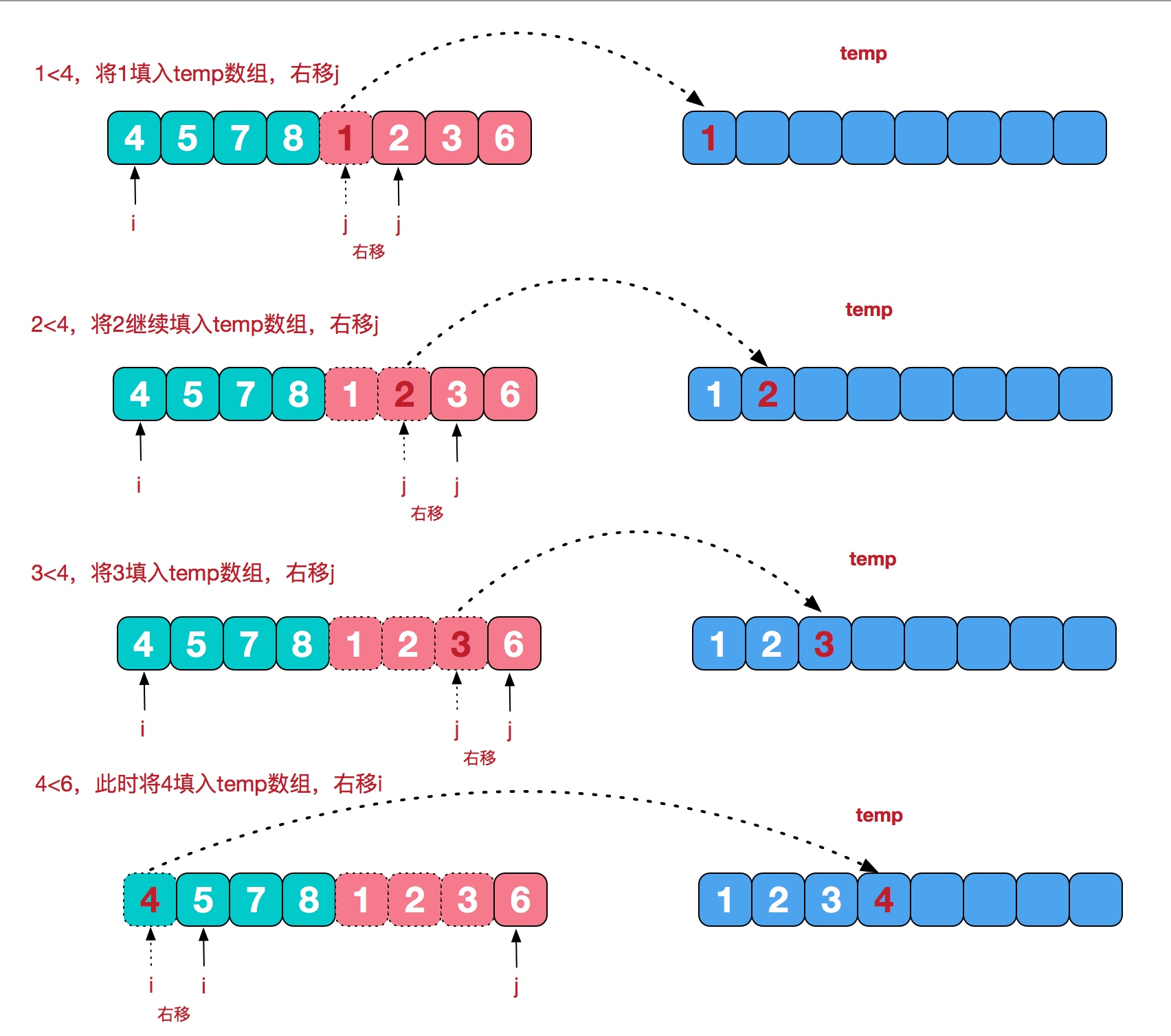
- 首先声明一个与原有数组相同的长度的临时数组 temp。
- 接着 i 指向子串 1 开始的位置,j 指向子串 2 开始的位置。接着比较 arr1[i] 与 arr2[j] 的值,找出较小值。因为两个子串都是有序的,所以这两个值中的最小值,就是整个串中的最小值。找出最小值后将其值放入 temp 的开始位置,最小值对应的子串下标加 1。这里可以看到是 4 < 1,即子串 arr2 的值较小,那么将 1 放入 temp[0] 位置,接着 j 加一,此时 j 指向 2。
- 接着继续对比 i 和 j 两个数的大小,继续对比步骤 2 的逻辑。这里可以看到 arr[i]=4 < arr[j]=2,那么应该将较小值放入 temp 数组中,即将 2 放入数组中,并且将 j + 1,即 j = 2,此时 j 指向的值 为 3。
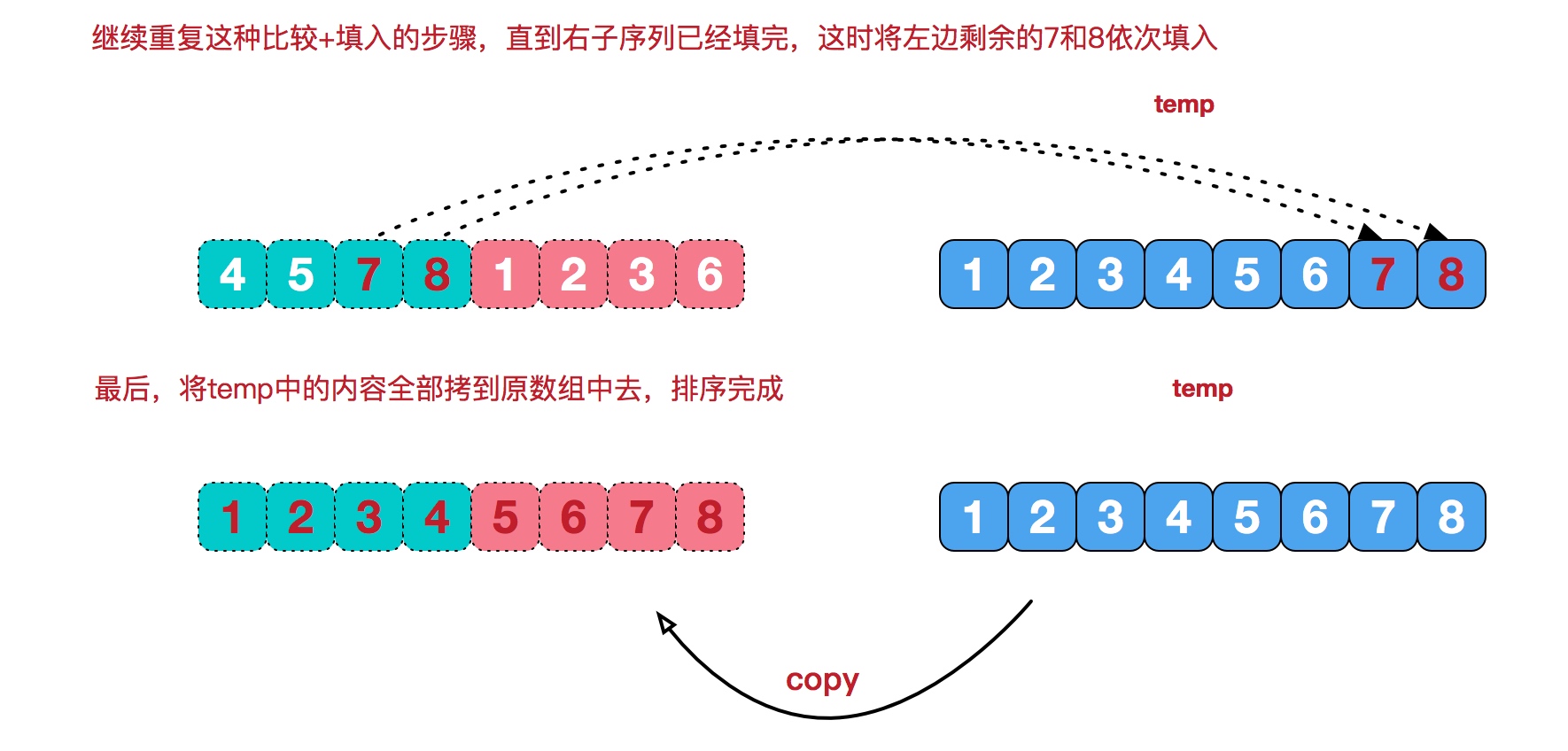
- 按着上述的步骤继续不断重复步骤 2 的内容,我们会看到子串 2 首先到末尾。此时子串 1 还剩下一些数值,这些数值肯定是更大的值,那么直接将这些数值复制到 temp 数组中即可。如果子串 1 先到末尾,那么就应该将子串 2 剩余的数值写入 temp 数组。
- 最后,将 temp 的数值写回原有数组中即可。
代码实现:
public static void sort(int []arr){
//在排序前,先建好一个长度等于原数组长度的临时数组,避免递归中频繁开辟空间
int []temp = new int[arr.length];
sort(arr,0,arr.length-1,temp);
}
private static void sort(int[] arr,int left,int right,int []temp){
if(left<right){
int mid = (left+right)/2;
//左边归并排序,使得左子序列有序
sort(arr,left,mid,temp);
//右边归并排序,使得右子序列有序
sort(arr,mid+1,right,temp);
//将两个有序子数组合并操作
merge(arr,left,mid,right,temp);
}
}
private static void merge(int[] arr, int left, int mid, int right, int[] temp){
//左序列指针
int i = left;
//右序列指针
int j = mid+1;
//临时数组指针
int t = 0;
while (i<=mid && j<=right){
if(arr[i]<=arr[j]){
temp[t++] = arr[i++];
}else {
temp[t++] = arr[j++];
}
}
//将左边剩余元素填充进temp中
while(i<=mid){
temp[t++] = arr[i++];
}
//将右序列剩余元素填充进temp中
while(j<=right){
temp[t++] = arr[j++];
}
t = 0;
//将temp中的元素全部拷贝到原数组中
while(left <= right){
arr[left++] = temp[t++];
}
}
可调试代码地址:java-code-chip/MergeSort.java at master · chenyurong/java-code-chip
参考:图解排序算法(四)之归并排序 - dreamcatcher-cx - 博客园
算法对比
选择排序与冒泡排序的区别?
选择排序是每次选出最值,然后放到数组头部。而冒泡排序则是不断地两两对比,将最值放到数组尾部。本质上,他俩每次都是选出最值,然后放到一边。
其最大的不同点是:选择排序只需要做一次交换,而冒泡排序则需要两两对比交换,所以冒泡排序的效率相对来说会低一些,因为会做多一些无意义的交换操作。
快速排序与归并排序的区别?
刚刚看了一下,快速排序和归并排序,我觉得差别可以提现在拆分合并的过程中,比较的时机。
快排和归并,都是不断拆分到最细。但是归并更纯粹,拆分时不做比较,直接拆!而快排还是会比较一下的。所以在拆分阶段,快排会比归并耗时一些。
而因为快排在拆分阶段会比较,所以其拆得没有归并多层级,因此其在合并阶段就少做一些功夫,会快一些。
所以快排和归并排序的区别,本质上就是拆分、合并的区别。
参考资料
文章首发于公众号「陈树义」及个人博客 shuyi.tech,欢迎关注访问。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号