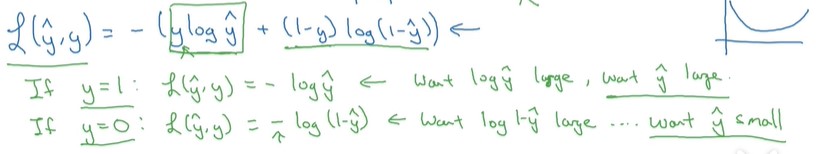神经网络
神经网络和深度学习[上]
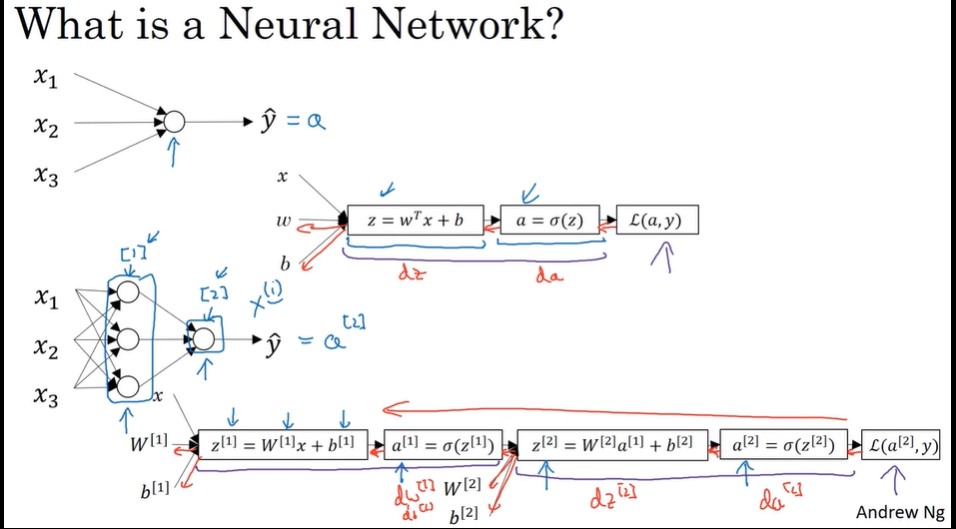
什么是神经网络？
假如我们要建立房价的预测模型，我们已知模型输入面积 x 及输出价格 y ，来预测房价：y = f(x)，我们用一条直线来拟合图中这些离散点（建立房价与面积的线性模型）。
这个简单的模型（蓝色折线）就是一个最简单的神经网络，该神经元的功能就是实现函数f(x)的功能。
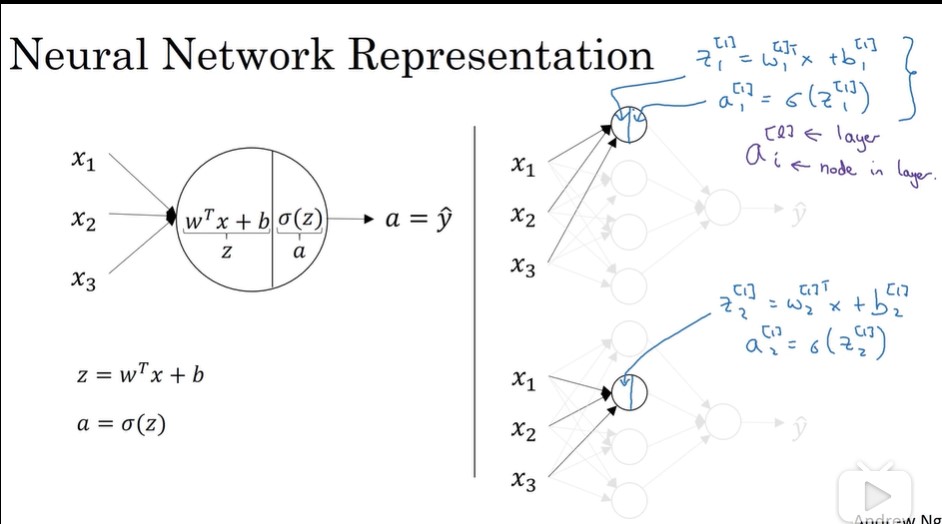
上面这个折线模型，可以用下面这个图表示，它也是最简单的模型：单神经网络。
比如，预测房屋的价格，可能有多种因素。这时，我们的神经网络就有多个输入。
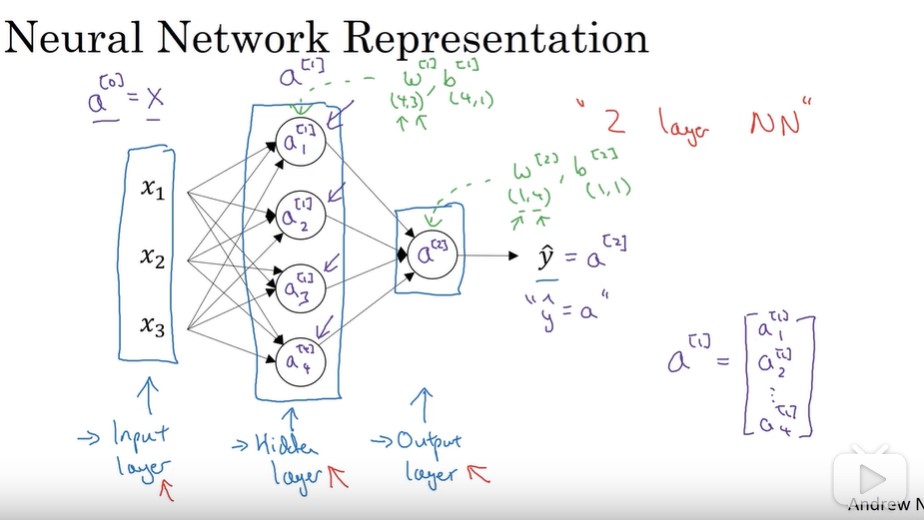
，每一个圈圈可以代表一个神经元（一个函数模型）。
我们把它画的整齐一点，隐藏层，中间的三个圈圈：
神经网络的编程基础
二分类
二分类就是输出 y 只有离散值 { 0, 1 }。以一个图像识别问题为例，判断图片中是否有猫存在，0 代表 non cat，1 代表 cat。这就是一个二分类问题。
逻辑回归
给定了输入特征 X，算法能够输出预测，可以记作y^,也就是对实际值y的估计。
用w表示逻辑回归的参数，w也是一个nx维向量(w实际是特征权重，维度与特征向量相同)，再加上实数b作为偏差，那么y^可以表示为：
y^=wTx+b
但是 这个函数的区间在负无穷~正无穷，为了让它属于(0,1)之间，我们也引入Sigmoid函数。
逻辑回归的损失函数
为了训练逻辑回归模型的参数w和参数b，需要一个代价函数。损失函数衡量了单个训练样本的表现。
简单的说明一下为什么损失函数是这样的形式。
当y = 1时损失函数为：L=−log(y^)，如果要想损失函数L尽可能得小，那么y^就要尽可能大，因为Sigmoid函数的取值范围是[0 1]，所以y^会无限接近于1。
当y = 0时损失函数为：L=−log(1−y^)，如果要想损失函数L尽可能得小，那么y^就要尽可能小，因为Sigmoid函数的取值范围是[0 1]，所以y^会无限接近于0。
成本函数
同理，成本函数衡量了在全部样本的训练表现
损失函数是在单个训练样本中定义的，它衡量的是算法在单个训练样本中表现如何，为了衡量算法在全部训练样本上的表现如何，我们需要定义一个算法的代价函数，算法的代价函数是对m个样本的损失函数求和除以m。
损失函数只适用于像这样的单个训练样本，而代价函数是参数的总代价，所以在训练逻辑回归模型时候，我们需要找到合适的w和b，来让代价函数J的总代价降到最低。
梯度下降法
要找到合适的w，b使其最小。需要通过梯度下降法。
最小梯度下降，沿它下降最快的方向 往下走
凸函数，可以用如图那个小红点来初始化参数w和b，也可以采用随机初始化的方法，对于逻辑回归几乎所有的初始化方法都有效，因为函数是凸函数，无论在哪里初始化，应该达到同一点或大致相同的点， 也是我们选择它做成本函数的原因。
下图中的 learning rate：控制每一次迭代的步长。
计算函数，关于某变量，在其方向上的斜率
计算图
一个神经网络的计算，都是按照前向或反向传播过程组织的。首先我们计算出一个新的网络的输出（前向过程），紧接着进行一个反向传输操作。后者我们用来计算出对应的梯度或导数。
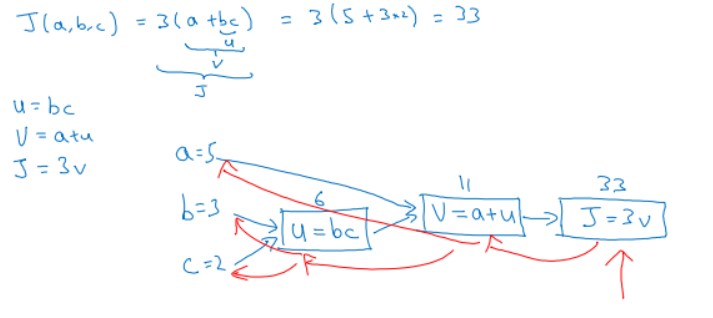
举个简单的例子，假如代价函数为J(a,b,c)=3(a+bc)，包含a，b，c三个变量。我们用u表示bc，v表示a+u，则J=3v。它的计算图可以写成如下图所示：
a=5，b=3，c=2。正向传播过程：
从左到右，则u=bc=6，v=a+u=11，J=3v=33
反向传播过程：
用到的链式求导法则，求得：
逻辑回归的梯度下降法（单个样本）
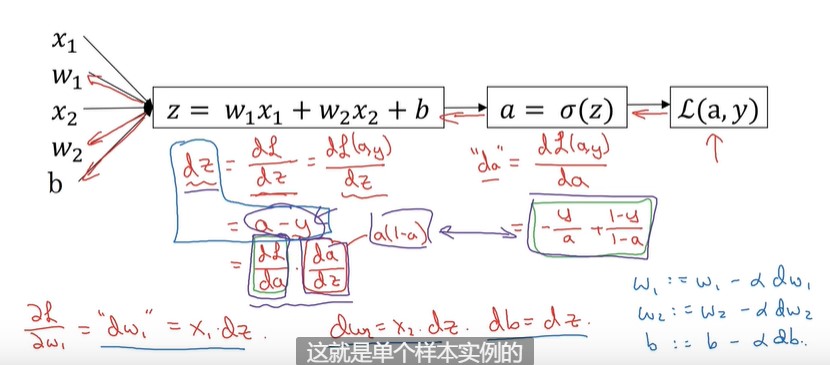
逻辑函数的几个方法如下：
假设该样本点有x1，x2两个特征
上面这种计算叫前向传播，来计算损失函数。
这时我们想要计算损失函数最小值，需要反向计算，。
也就是反着计算。
dz ，dw1，dw2，db= 。。。
再更新
w1 = ，w2，b的值。
这个计算过程就是单个样本实例的梯度下降中参数更新一次的步骤。
m个训练样本的梯度下降法
成本函数如下所示：
这样需要依次计算dw1...dwn，太过麻烦。所以就用到了向量化。
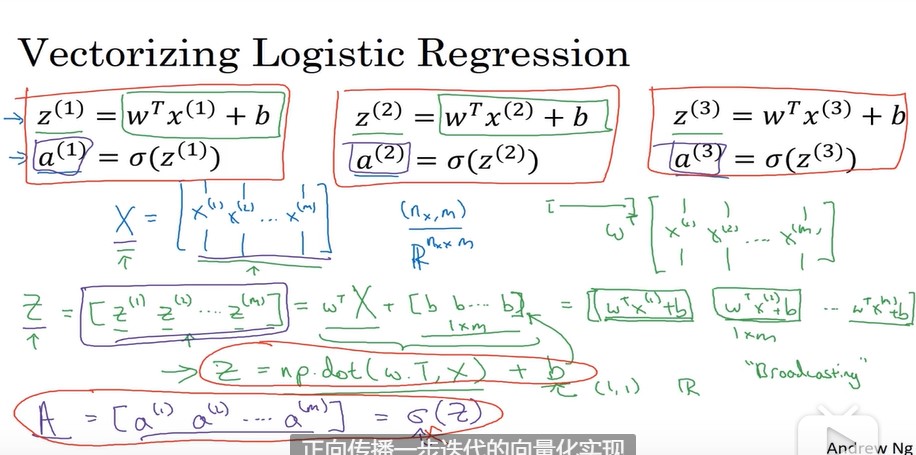
向量化逻辑函数
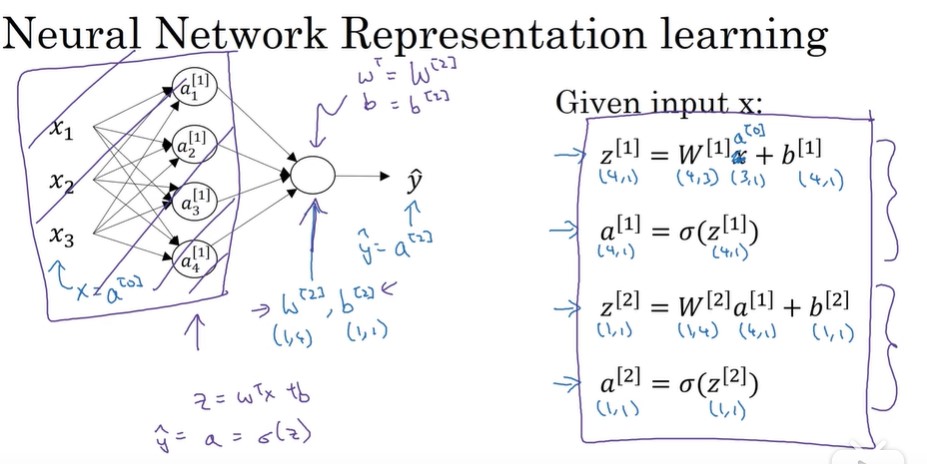
假设有m个样本，则前向传播过程中，对样本的预测是
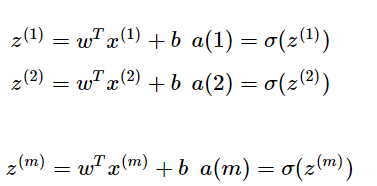，假设有m个样本，则需要进行m次操作，所以定义x。x表示m列（样本数）n行（特征数）的矩阵。计算过程如下所示：
神经网络概述
多个样本向量化
方括号，第二层。 小括号 ，第n个样本
对于A矩阵，x轴代表 样本数 ，纵坐标代表 隐藏的单元数。
激活函数：
而在实际中，基本不使用阿尔法函数
