数字预失真设计---基于神经网络

1.直接学习和间接学习预失真架构的比较

 

 

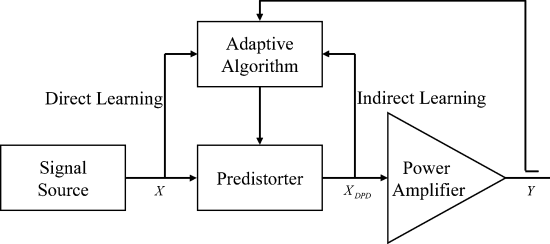
 分开表示：

 

间接学习模型示意图：

 

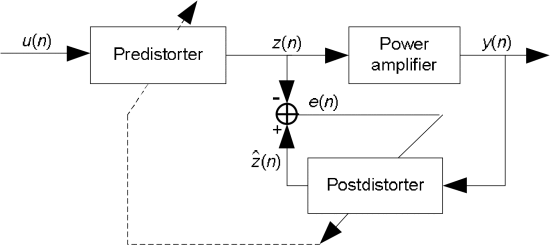
直接学习模型示意图：

 

 

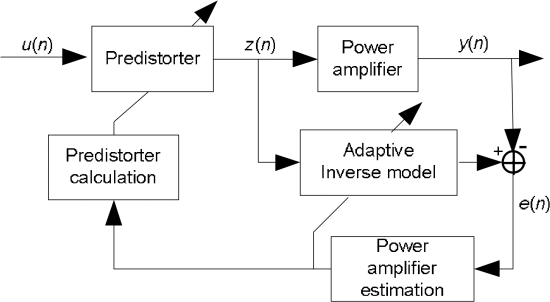
 直接学习架构中，首先使用类似于下式记忆多项式对 PA 模型进行建模。其次，计算PA模型的逆。

 

 

 

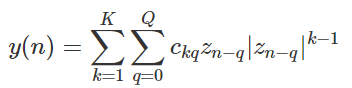
 因此，PD 函数可以表示为：

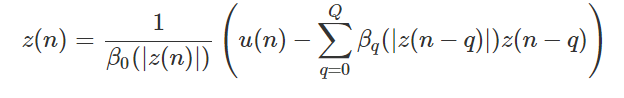其中：

 

 

 

 

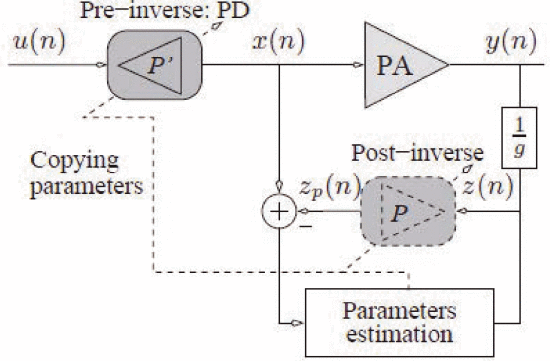
通过 PA 的神经网络模型反向传播的神经网络 DPD

校正 PA 中非线性的常用方法是通过数字预失真 (DPD)，其中学习 PA 非线性，以便在数字基带中应用逆向。

大多数 DPD 工作依赖于某种形式的记忆多项式 (MP) 来创建预失真器尽管它们的性能可能足够，

但使用广义记忆多项式 (GMP) 实现这种性能所需的计算复杂度可能非常高，有时需要数百个系数。

众所周知，神经网络 (NN) 能够根据通用逼近定理学习任意非线性函数。

考虑到 DPD 是非线性函数，很自然地考虑使用 NN 进行预失真，并且许多工作已经将 NN 应用于 DPD 

NN 实现和大多数其他 DPD 工作依赖于间接学习架构 (ILA) 来训练预失真器。学习后失真器容易受到反馈信号中噪声的影响，并且不一定会收敛到最好的预失真器。

NN DPD 系统的架构：

 

 

 

 

 

 

 

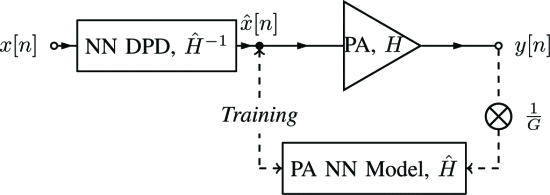
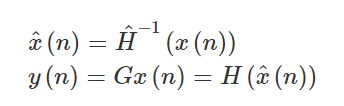
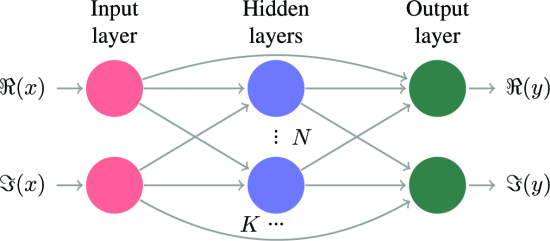
 具有K个隐藏层和每个隐藏层N个神经元的 NN 的一般结构。信号的实部和虚部总是有两个输入和输出神经元。

输入通过跳跃连接连接到输出神经元，以便隐藏层集中在信号的非线性部分。

神经网络设计:

两个独立的 NN：一个 DPD NN，将用于对实际 PA 进行预失真，以及一个 PA NN 模型，用于训练 DPD NN。

为了简单起见，我们保持这些 NN 的设计相同。但是，由于 PA NN 仅在 DPD 训练阶段使用，因此可以任意复杂化以提高逆模型的准确性。

 

由于基带信号很复杂，将 NN 设计为具有两个输入神经元和两个输出神经元：一个神经元用于信号的实部，一个用于虚部。

然后，至少有一个具有校正线性单元 (ReLU) 激活函数的全连接隐藏层。这里可以选择 ReLU 激活函数，是因为它们的实现复杂度低。

算法：