谐波失真与积分非线性的关系——直方图测试确定 DNL 和 INL 错误,基于正弦波
谐波失真与积分非线性的关系
系统包含模数转换器。经常在这些设备的数据表中看到信噪比和总谐波失真的规格。如果主要关心线性,这些数字对我有用吗?
这不是一个容易回答的问题。在线性度是关键问题的许多设计中,最好的答案是“不,这些规范对您没有用处”。
然而,答案是“是的,它们很有用”的情况很重要,并有助于说明在为给定任务指定 ADC 时如何使用动态规范。
首先,让我们定义几个术语。我假设“线性” 是指微分非线性(DNL)和积分非线性(INL)。
这两个规范有不同的含义,但直接相关。术语线性也可以仅指 INL。这里的主要兴趣是 INL,但我们也会在某种程度上涵盖 DNL。
另一个术语是“工业 ADC”。 这是一个专注于线性度得到充分保证和测试的转换器的细分市场。这些通常是转换速率为几兆赫兹及以下的 ADC。
作为比较,音频 ADC 和超高速 ADC(5MHz 及以上)可能会提供典型的线性规范,但不能保证设备的实际性能。
关于各种规格,差分非线性是衡量每个单独输出代码的“大小”与理想代码大小有何不同的量度。积分非线性是衡量转换器的整体传递函数如何偏离完美线性(直线)传递函数的量度。
现在,让我们看看如何测试工业 ADC。实现此目的的一种技术是将 ADC 置于伺服环路布置中。此设置的目标是为 ADC 提供稳定的(“DC”)输入电压,以便在 50% 的时间产生目标代码,并在 50% 的时间产生下一个更高的代码(这称为“查找代码”边缘”)。一旦达到这一点,就测量 ADC 输入端的电压。测试继续使用下一个更高的代码,直到测试所有代码。从测量的电压阵列中,计算增益误差、偏移误差、DNL 和 INL 是一件简单的事情。其他测试方法也依赖于缓慢变化的输入信号。
请注意,此测试方法不测试 ADC 的采样保持性能。由于输入电压稳定或移动非常缓慢,因此甚至不需要采样保持。曾经,采样保持器是独立于 ADC 的分立器件。目前,几乎所有 ADC 都包含采样保持功能,因此很容易忘记它们有自己的一套规范。
这给我们带来了“动态”规范。这些规格包括信噪比 ( SNR )、信噪比 ( SINAD )、总谐波失真 ( THD ) 和无杂散动态范围 ( SFDR )。在本次讨论中,我们将忽略 SFDR,但只要说它与 THD 直接相关就足够了。此外,SINAD 是 SNR 和 THD 的 RMS 和,因此我们也将忽略该规范。
现在,我们需要看看 THD 和 SNR 的含义。在动态测不是剪辑)。然后将得到的数据从时域转换到频域。理想情况下,频域将显示输入信号(称为“基波”)和转换器的量化噪声(称为“本底噪声”),仅此而已。实际转换器的频谱将显示许多信号或音调超出本底噪声。其中一些音调与输入信号谐波相关(输入信号的两倍、三倍等)。
信噪比是输入信号的功率与本底噪声的总功率之比,不包括基波的 N 个谐波(N 通常为 3 到 9)。 总谐波失真是基波前 N 个谐波的总功率。THD 可以相对于转换器的满量程输入范围 (dBFS) 或相对于输入信号 (dBc,“相对于载波的 dB”) 来表示。许多制造商仅列出技术上不正确的“dB”。但是,如果输入信号几乎覆盖了转换器的输入范围,则 dBFS 基本上等于 dBc。
好吧,那么这一切意味着什么?好吧,不用深入所有的数学,可以证明转换器的 SNR 与 DNL 直接相关, 而THD 与 INL 直接相关。
这似乎意味着只要保证 INL 和 DNL,SNR 和 THD 对于工业 ADC 来说并不重要。
然而,ADC 的 THD与输入信号的频率直接相关。在某个频率以下,THD 仅取决于转换器的整体 INL. 高于该频率,THD 越来越依赖于转换器的采样保持性能。由于 THD 与 INL 相关,因此转换器的 INL 也会恶化,并与采样保持的性能直接相关。
最终结果是,超过一定的输入频率,数据手册中保证的INL就没有意义了。(请注意,SNR 随输入频率的变化非常轻微,因此 DNL 也是如此。但是,在大多数工业 ADC 中,这种影响通常可以忽略不计。)
让我们看一些例子。图1中的图表A和B显示了 INL较差的转换器的 INL以及该转换器的 THD。图C和D显示了完全相同类型的转换器的 INL,但INL 更好。可以看出,第二个转换器的 THD 明显优于第一个转换器。转换器具有相同的采样保持性能,THD 的差异完全取决于转换器的线性度。(出于好奇,所示的 ADC 是一个12 位、200kHz 的ADC)。
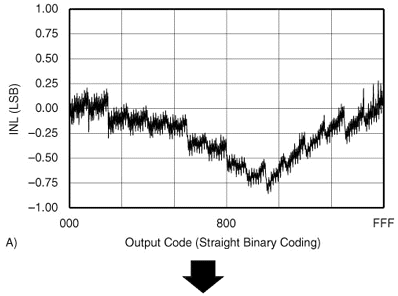
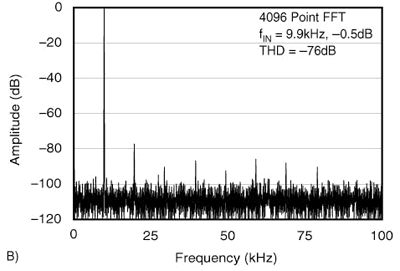
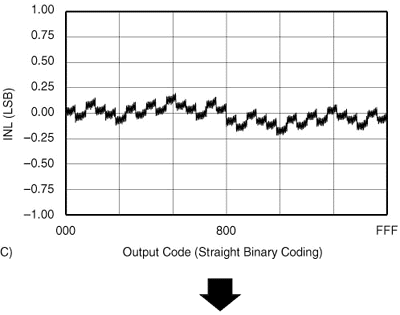
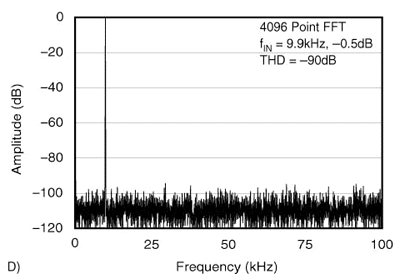
现在我们已经在THD和INL之间建立了联系,让我们看看这意味着什么。
转向不同的转换器(16 位、40kHz ADC),图 2显示了数据表中的典型性能曲线 - THD 与输入频率的关系。可以看出,该转换器的 THD 性能随着输入频率的增加而显着恶化。
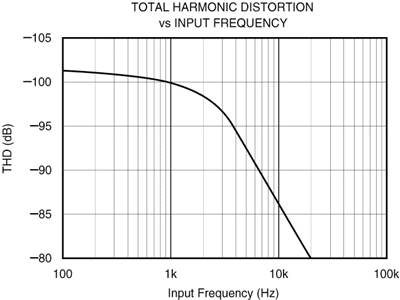
该器件的 INL 规范仅适用于低频输入,即图 2中图表的最左侧。随着输入频率的增加,INL 会恶化。现在是回顾 INL 定义的好时机:输出代码与转换器理想传递函数的偏差。因此,随着输入信号频率的增加,输出代码将越来越偏离所需的理想输出代码。
例如,如果图 2中描述的转换器用于数字化可以以与 10kHz 信号等效的速率转换的信号,则转换器的“THD”性能将大约为 -86dB。这个数字意味着谐波失真比转换器的满量程范围低 86dB。由于这个 16 位转换器的满量程范围为 ±32,768,因此谐波失真代表大约 ±1.6 LSB 的误差。
我们在这里必须非常小心。如果转换器在极低频率下的性能也是 -86dB,那么 INL 已经包含 -86dB THD 数,因此我们不必将 THD 作为因素考虑。我们只关心 THD 恶化了多少。在图 2 中,转换器的低频 THD 约为 -101dB。这表示 INL 误差为 ±0.3 LSB。因此,INL 误差实际上只增加了 ±1.3 LSB。(请记住,此计算是一阶近似值。根据谐波及其相位关系,实际误差可能会有所不同。)
然后,最坏情况的计算将包括 ±2 LSB(此特定设备的高等级)加上 ±1.3 LSB 的 INL 规范。它还必须包括另一个我们尚未讨论的项目:来自 ADC 的内部噪声。这增加了额外的 ±2.4 LSB 误差。因此,16 位转换器已从 ±2 LSB 的 INL 变为 ±5.7 LSB 的误差!
许多“工业”系统的设计者可以放心地忽略 THD 的原因是工业过程通常不是很高的速度。此外,工业 ADC 的采样保持性能差异很大。一些 ADC 完全不受其采样保持的限制。其他的仅限于一定程度。
底线是考虑输入信号的最大转换速率。然后,查看器件数据表中 SNR 和 THD 的典型性能曲线。如果这两条曲线在输入信号的频率范围内都是平坦的,那么您可以专注于转换器的 INL 和 DNL 规格。请记住,您可能必须将最大转换速率转换为等效频率。此外,不要忘记将转换器的内部噪声作为误差源,尤其是对于高分辨率转换器(16 位及以上)。
直方图测试确定 DNL 和 INL 错误
直方图测试确定 DNL 和 INL 错误
如今,数据转换器制造商经常使用直方图方法来验证其数据转换器的积分 (INL) 和差分 (DNL) 非线性规范。这种方法,也称为代码密度测试,是在数据转换器的幅度域中执行的。在直方图测试期间,具有浴缸分布的重复动态信号(例如正弦波信号)被施加到模数转换器 (ADC),在转换器的输出端生成相应的数字代码分布。与相应的输出代码分布的任何偏差都会导致可以使用直方图方法估计的各种错误。这些错误参数首先包括 DNL 和 INL。
对于 ADC,给定模拟输入信号,直方图显示每个不同数字代码字在 ADC 输出上出现的次数。直方图测试的一种方法涉及对正弦输入信号进行采样和数字化。然后将数字化信息分类到代码箱中。每个代码仓代表一个输出代码。根据输入信号,收集每个 bin 的样本数或命中数。N 代表 ADC 的分辨率或总位数,将有 2 N个码箱。对于理想的 ADC,每个代码仓宽度应对应于 FSR/2 N的位宽,其中 FSR 是 ADC 的满量程范围,单位为伏特。然而,在现实世界中,ADC 的代码仓宽度可能并不相同。例如,如果在代码仓中收集的样本(对于已知输入信号)的数量大于预期,那么这个数字将表明代码仓宽度大于理想值(从统计上讲)。
代码样本的频率显示为代码的函数。对于理想的 ADC,该图将是正弦波的概率密度函数 p(V),表示如下
p(V) = 1 / ( π
× √[A² - V² ])必须确定样本数组的大小。
但是什么大小的数据记录代表了具有统计意义的样本数量呢?
概率密度函数将有助于回答这个问题。对于给定的概率密度函数和数据记录大小,理想 ADC 的每个代码仓都标识了预期的样本数量及其相关的标准偏差。代码仓中的样本数量接近预期水平的置信度等于样本落入适当偏差数量内的概率。请注意,标准偏差与预期值之间的比率会随着数据记录中样本数量的增加而降低。为了获得整个范围的置信度,将所有代码落在所需代码内的概率相乘。
要计算记录数据阵列的每个代码的概率,需要将每个代码的样本数除以数据记录中的样本数。理想的采样概率是理想 ADC 在转换器输入端应用纯正弦波时所产生的概率。对基于正弦波的输入信号的概率密度函数在 bin 数量上进行积分允许每个代码 bin 的确切大小计算如下
P(n) = 1/ π × [arcsin(FSR × {n-2 N-1 } / A × 2 N ) - arcsin(FSR × {n-1-2 N-1 } / A × 2 N )],
其中 n 表示代码 bin 编号,FSR 是满量程范围,N 是 ADC 的分辨率。每个输出代码处测量(实际)直方图与理想直方图之间的偏差是代码大小的函数,可用于确定数据转换器的 DNL。DNL 可计算如下
DNL (LSB) = [AP(n th code) / IP(n th code)] -1
其中 n 代表码元数,范围从 1 到 2 N,N 是 ADC 的分辨率, AP(n th code) 表示代码 bin n 中样本的测量直方图,IP(n th code) 是代码 bin n 中样本的理想(预期)直方图。
不幸的是,直方图方法需要捕获相当大的数据记录。所需的样本数量取决于 ADC 的分辨率、所需的测量置信水平以及 DNL 误差的大小。例如,DNL 误差 (β) 为 0.1LSB 和 95% 置信水平 (Z α /2 ) 的 10 位 ADC 需要记录超过 50 万个样本 (N RECORD )。将置信度从 95% 提高到 99% 将导致超过一百万个样本的数据记录大小显着增加。
N记录= π × 2 N-1 × (Z α /2 )²] / β² = π × 2 9× (1.96)² / (0.1)² = 617,920
N RECORD = π × 2 N-1 × (Z α /2 )²] / β² = π × 2 9 × (2.58)² / (0.1)² = 1,070,678
随着 ADC 分辨率的增加,为满足置信水平和误差分辨率所需的样本数量将乘以两倍于转换器分辨率中添加的每一位。对于具有 12 位及更高分辨率的 ADC,此测试最终可能成为测量 DNL 的限制因素,因为它需要海量数据存储能力来托管所需的超过 400 万个数据点。尽管记录大小和分辨率的增加会导致实验室和生产测试时间延长带来的不良和成本密集型副作用,但引入所谓的硬件直方图生成器可以帮助减少测试时间。此类发生器的测试时间定义为记录大小与 ADC 采样率之间的比率。
通过直方图方法确定 DNL 可能具有挑战性,因为该测试对输入正弦波的幅度变化、噪声、时钟抖动和转换器滞后很敏感。在这种情况下,使用累积直方图测试可能是计算 INL 和 DNL 误差的更好选择。为此,必须确定 ADC 的偏移和转换电压。为了在数字化数据点的集合中找到偏移误差,将数据记录中的正样本和负样本的数量相等(N RECORD = N RECORD[P] + N RECORD[N])如下
2 N-1
N RECORD[ N] = ΣAP(第 n个代码)
n=1
2 N
NRECORD[P] = Σ AP(n th code)
n=2 N-1 + 1
V OFFSET = 0.5 × A × π × sin[(N RECORD[P] -N RECORD[N] ) / (N RECORD[P ] + N RECORD[N] )]
计算出偏移误差后,转换电压或代码边沿 (V j ) 可以通过使用以下数学表达式
j
V j = -A × cos [ π × (Σ AP(n th代码) / N RECORD )]
n=1
在已知转换电压的情况下,INL 和 DNL 参数的计算变得独立于正弦波信号的输入幅度,可以使用以下公式计算
j
INL j (LSB) = Σ DNL j (LSB)
n=1
DNL j (LSB) = (V j+1 - V j ) × (2 N /FSR)
其中 DNL j是两个相邻码之间的差值,INL j表示所有 DNL j错误的总和。FSR 是满量程范围,N 是测量 INL 和 DNL 的 ADC 的分辨率。
下图显示了 8 位、低功耗 45Msps ADC MAX1193 的直方图、INL 和 DNL 性能。对于 MAX1193,INL 和 DNL 测试采用 5.6018MHz 正弦输入信号进行。请注意,图 1表示了足够数量和不足数量的代码计数之间的直方图比较。图 2和图3描述了在这些(足够和不足的样本量)条件下得到的 DNL 和 INL 性能。
图 1. 代码计数充足与代码计数不足直方图显示。
图 2. 代码数量充足与代码数量不足时的 DNL 差异 。
图 3. 代码数量充足与代码数量不足时的 INL 差异。



