排序

目录

• 排序算法分类
  • 原址排序
  • 稳定排序
  • 比较排序
  • 比较排序算法
    • 冒泡排序 Bubble Sort
    • 选择排序 Selection Sort
    • 插入排序 Insertion Sort
    • 快速排序 Quick Sort
    • 归并排序 Merge Sort
    • 堆排序 Heap Sort
  • 非比较排序算法
    • 计数排序
    • 基数排序
    • 桶排序
• 总结

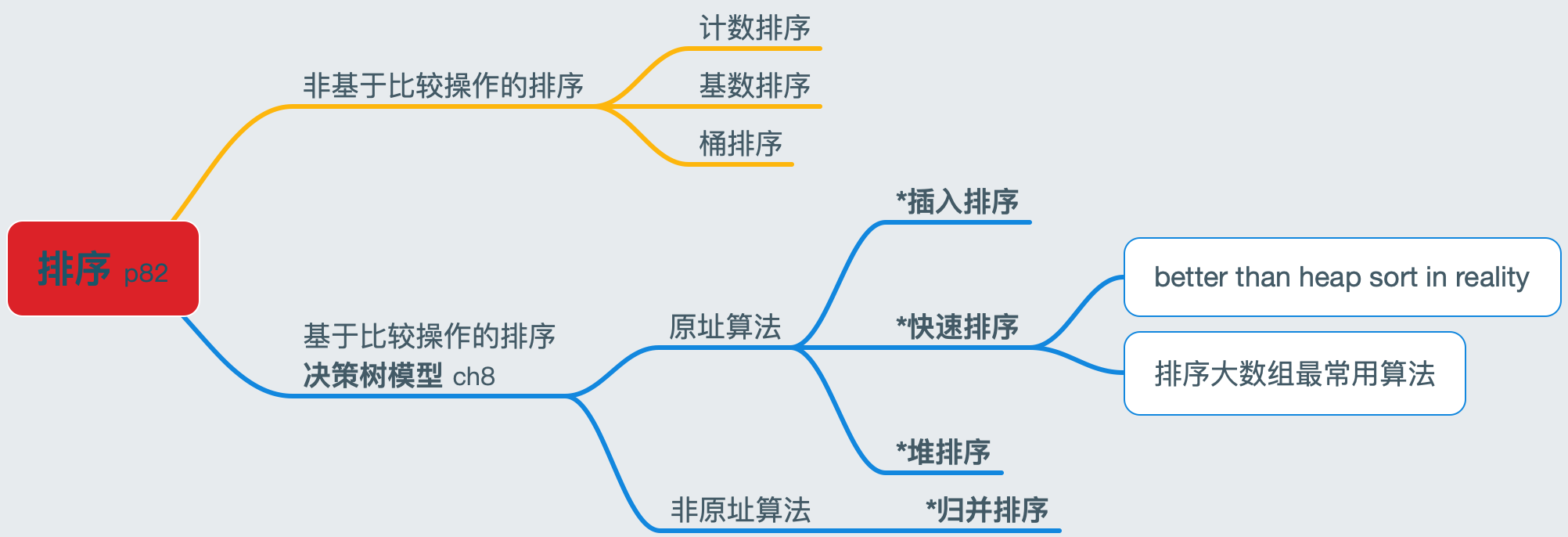
排序算法分类

原址排序

如果输入数组中仅有常数个元素需要在排序过程中存储在数组之外，则称排序算法是原址的 (in place)。插入排序，选择排序，堆排序，快速排序都是原址的。归并排序不是原址的。

稳定排序

如果输入数组中相同键值的元素在排序后的相对次序不变，那么该排序就是稳定的。

比较排序

插入排序、归并排序、堆排序及快速排序都是比较排序算法：它们都是通过对元素进行比较操作来确定输入数组的有序次序。

使用决策树模型，我们可以证明任意比较排序算法排序 \(n\) 个元素的最坏情况运行时间下界为 \(\Omega(nlgn)\)，从而证明堆排序和归并排序是渐进最优的比较排序算法。如果有额外信息可以不通过比较操作来获得输入序列的次序信息，就有可能打破 \(\Omega(nlgn)\) 的下界。

本文将介绍几种常见的比较排序算法，然后介绍基于特殊序列的非比较操作排序算法，并给出它们的时间复杂度。

比较排序算法

冒泡排序 Bubble Sort

冒泡排序算法正如其名字，每遍历一轮所有元素，待排序序列中最大（小）的元素，像气泡一样浮到最上面（待排序元素的最后）。在上浮的过程中，遇到比当前气泡更大的元素，该气泡就停止上浮，换由更大的元素继续上浮。

void bubble_sort(vector<int> &arr) {
  int len = arr.size();
  for (int end = len - 1; end >= 0; end--) {
    for (int i = 1; i <= end; i++) {
      if (arr[i - 1] > arr[i]) {
        swap(arr[i], arr[i - 1]);
      }
    }
  }
}

时间复杂度：$ O(n^2) $
空间复杂度：$ O(1) $

选择排序 Selection Sort

选择排序算法是选择待排序序列中的最大（小）的元素，与待排序序列的最后位置的元素交换位置，随着排序的进行，所有元素最终有序。

void selection_sort(vector<int> &arr) {
  int len = arr.size();
  int tgt;
  for (int end = len - 1; end > 0; end--) {
    tgt = 0;
    for (int i = 1; i <= end; i++) {
      if (arr[i] >= arr[tgt]) {
        tgt = i;
      }
    }
    swap(arr[end], arr[tgt]);
  }
}

时间复杂度：$ O(n^2) $
空间复杂度：$ O(1) $

插入排序 Insertion Sort

插入排序算法中“插入”的含义就是把待排序元素插入到数组中已排序的部分。如果该元素比已排序部分都大，则插入到已排序部分最后；如果插入已排序部分的中间或者头部，则需要部分或全部已排序元素后移 1 位。

void insertion_sort(vector<int> &arr) {
  int len = arr.size();
  int end, i;
  for (end = 1; end < len; end++) {
    int tgt = arr[end];
    for (i = end - 1; i >= 0; i--) {
      if (tgt >= arr[i]) {
        break;  // insert position (i + 1)
      }
      arr[i + 1] = arr[i];  // right shift
    }
    arr[i + 1] = tgt; 
  }
}

时间复杂度：$ O(n^2) $
空间复杂度：$ O(1) $

快速排序 Quick Sort

快速排序算法在每轮排序之后，总会有至少一个元素位于排序后的最终位置处，并且，该元素位置之前都是比其小的元素，之后都是比其大的元素。简而言之，该算法是“先整体有序，再局部有序”的过程。显然，局部有序是整体有序的一部分，递归的使用顺其自然。

// index range [l, r]
static void helper(vector<int> &arr, int l, int r) {
  if (r <= l) {
    return;
  }

  swap(arr[rand() % (r - l + 1) + l], arr[r]);
  int k = l;
  for (int i = l; i < r; i++) {
    if (arr[i] < arr[r]) {
      swap(arr[k++], arr[i]);
    }
  }
  swap(arr[k], arr[r]);
  helper(arr, l, k - 1);
  helper(arr, k + 1, r);
}

void quick_sort(vector<int> &arr) {
  helper(arr, 0, arr.size() - 1);
}

在最坏情况下，如果数组逆序，恰好每次都取到最后一个元素来比较，那么快排的时间复杂度相较插入排序没有特别优势。除此之外，快速排序每轮排序都随机选择比较位置，在数组元素随机排列的情况下，期望时间复杂度相较插入排序就有很大改善。在实际应用中，快排的速度还是很快的，也得到了大规模应用。Python sort 库函数就是快排和插入排序的组合排序。

时间复杂度：$ O(nlogn) $ 期望
空间复杂度：$O(1) $

归并排序 Merge Sort

归并排序算法是将数组分为两个子数组分别排序，然后再将有序子数组合并。显然，每个子数组排序也适用归并排序。因此，归并排序是“先局部有序，再整体有序”的过程。不同于以上原址排序，归并排序需要等同数组大小的额外空间，存储有序的子数组部分，然后合并子数组覆盖原数组，而不能用子数组合并覆盖其本身。

void merge(vector<int> &arr, int l, int m, int r, vector<int> &tmp) {
  int i= l, j = m;
  int k = l;
  while (i < m && j < r) {
    if (arr[i] < arr[j]) {
      tmp[k++] = arr[i++];
    } else {
      tmp[k++] = arr[j++];
    }
  }
  while (i < m) {
    tmp[k++] = arr[i++];
  }
  while (j < r) {
    tmp[k++] = arr[j++];
  }
  arr = tmp;
}
// index range [l, r)
static void helper(vector<int> &arr, int l, int r, vector<int> &tmp) {
  if (r - l < 2) {
    return;
  }
  int m = l + (r - l) / 2;
  helper(arr, l, m, tmp);
  helper(arr, m, r, tmp);
  merge(arr, l, m, r, tmp);
}

void merge_sort(vector<int> &arr) {
  vector<int> tmp = arr;
  helper(arr, 0, arr.size(), tmp);
}

时间复杂度：$ O(nlogn) $
空间复杂度：$O(n) $

堆排序 Heap Sort

堆排序算法是构建最大（小）堆，然后每次取出堆顶值，再次构建最大（小）堆，直到最后一个元素。所谓堆，就是将数组中元素构建成一个具有根节点数据比左右节点数据都大（小）的完全二叉树。

// index range [l, r)
static void heapify(vector<int> &arr, int i, int end) {
  int l = 2 * i + 1;
  int r = 2 * i + 2;
  int k = i;
  if (l < end && arr[l] > arr[i]) {
    k = l;
  }
  if (r < end && arr[r] > arr[k]) {
    k = r;
  }
  if (k != i) {
    swap(arr[k], arr[i]);
    heapify(arr, k, end);
  }
}
static void construct_heap(vector<int> &arr) {
  int len = arr.size();
  for (int i = len / 2; i >= 0; i--) {
    int l = 2 * i + 1;
    int r = 2 * i + 2;
    if (l < len && arr[l] > arr[i]) {
      swap(arr[l], arr[i]);
    }
    if (r < len && arr[r] > arr[i]) {
      swap(arr[r], arr[i]);
    }
  }
}
void heap_sort(vector<int> &arr) {
  int len = arr.size();  
  construct_heap(arr);
  for (int i = len - 1; i > 0; i--) {
    swap(arr[0], arr[i]);
    heapify(arr, 0, i);
  }
}

时间复杂度：$ O(nlogn) $
空间复杂度：$ O(1) $

非比较排序算法

计数排序

计数排序算法假定输入元素的值均在集合 \(\{0, 1, ..., k\}\) 内。通过使用数组索引作为确定相对次序的工具，计数排序可以在 \(\Theta(k+n)\) 的时间内将 \(n\) 个数排好序。因此，当 \(k=O(n)\) 时，计数排序算法的运行时间与输入数组的规模呈线性关系。

基数排序

另外一种相关的排序算法——基数排序，可以用来扩展计数排序的适用范围。如果有 \(n\) 个整数要进行排序，每个整数有 \(d\) 位数字，并且每个数字可能取 \(k\) 个值，那么基数排序就可以在 \(\Theta(d(n+k))\) 时间内完成排序工作。当 \(d\) 是常数且 \(k=O(n)\) 时，基数排序的运行时间就是线性的。

桶排序

桶排序算法需要了解输入数组中数据的概率分布。对于半开区间 \([0,1)\) 内服从均匀分布的 \(n\) 个实数，桶排序的平均运行时间为 \(O(n)\)。

总结

基于以上，排序的时间复杂度对比情况如下表：

算法	最坏情况运行时间	平均情况/期望运行时间
冒泡排序	$\Theta(n^2) $	$ \Theta(n^2) $
选择排序	$\Theta(n^2) $	$ \Theta(n^2) $
插入排序	\(\Theta(n^2)\)	\(\Theta(n^2)\)
归并排序	\(\Theta(nlgn)\)	\(\Theta(nlgn)\)
堆排序	$O(nlgn) $	$ \Theta(nlgn) $
快速排序	\(\Theta(n^2)\)	\(\Theta(nlgn)\)
计数排序	\(\Theta(k+n)\)	\(\Theta(k+n)\)
基数排序	\(\Theta(d(k+n))\)	\(\Theta(d(k+n))\)
桶排序	\(\Theta(n^2)\)	\(\Theta(n)\) (平均情况)