[BZOJ1036][ZJOI2008]树的统计Count
1036: [ZJOI2008]树的统计Count
Time Limit: 10 Sec Memory Limit: 162 MBSubmit: 10191 Solved: 4131
[Submit][Status][Discuss]
Description
一棵树上有n个节点,编号分别为1到n,每个节点都有一个权值w。我们将以下面的形式来要求你对这棵树完成一些操作: I. CHANGE u t : 把结点u的权值改为t II. QMAX u v: 询问从点u到点v的路径上的节点的最大权值 III. QSUM u v: 询问从点u到点v的路径上的节点的权值和 注意:从点u到点v的路径上的节点包括u和v本身
Input
输入的第一行为一个整数n,表示节点的个数。接下来n – 1行,每行2个整数a和b,表示节点a和节点b之间有一条边相连。接下来n行,每行一个整数,第i行的整数wi表示节点i的权值。接下来1行,为一个整数q,表示操作的总数。接下来q行,每行一个操作,以“CHANGE u t”或者“QMAX u v”或者“QSUM u v”的形式给出。 对于100%的数据,保证1<=n<=30000,0<=q<=200000;中途操作中保证每个节点的权值w在-30000到30000之间。
Output
对于每个“QMAX”或者“QSUM”的操作,每行输出一个整数表示要求输出的结果。
Sample Input
1 2
2 3
4 1
4 2 1 3
12
QMAX 3 4
QMAX 3 3
QMAX 3 2
QMAX 2 3
QSUM 3 4
QSUM 2 1
CHANGE 1 5
QMAX 3 4
CHANGE 3 6
QMAX 3 4
QMAX 2 4
QSUM 3 4
Sample Output
1
2
2
10
6
5
6
5
16
HINT
Source
这道题是裸的树链剖分。
不知道什么是树链剖分?简而言之,就是把一棵树用knife剖成几条链,然后通过对链上信息的维护、查询来完成有关树的操作。但是,这种剖分不能任意进行,否则时间复杂度可能很高,有时与暴力差不了多少。
还好,我们的先人们给出了一种伟大的剖分方式,这种剖分叫做轻重路径剖分。它的时间复杂度十分优秀,几乎所有的询问、修改都可以在$O(\log n)$的时间内完成。在进行剖分之前,我们要进行一些必要的预处理——比如计算出每个点$x$的父亲结点$father[x]$,儿子结点(不止一个,可以用动态数组存储)$sons[x]$,深度$depth[x]$,以该点为根的子树中结点的个数$sum[x]$等等,这都是树的基本操作,在此不再赘述。
然后就要开始定义了:对于任意一个非叶结点$x$,找出它的所有儿子节点$y \belongto sons[x]$中$sum[y]$最大的结点,把连接$x,y$的边称为重边。这样对每个非叶结点$x$,都有一条重边与之对应,我们在图中标记出这些重边:
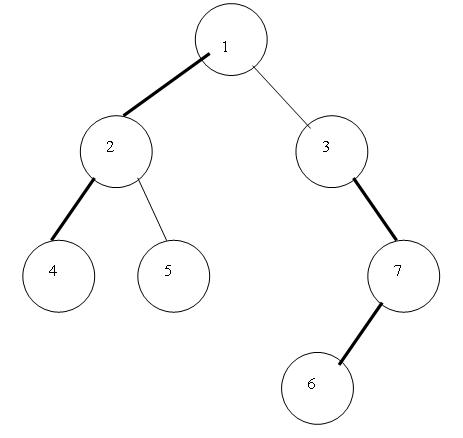
这些重边连成了链!我们就把树剖分成这些链。注意某些叶子节点不与任何重边相连,它自成一条链。我们再规定除了重边以外,所有边均叫做轻边。
剖分完毕之后,对于每条链上的数据,我们可以用线段树维护,这样就可以方便地单点修改、区间修改、区间查询了。
虽然说起来容易,但代码量不小,完全可以做一些比赛前的练手题。注意,本题还是有点坑,因为点权可能为负数,所以计算最大值时,要把初始值赋为-INF,如果设成0就会WA。
代码:

1 /************************************************************** 2 Problem: 1036 3 User: GodCowC 4 Language: C++ 5 Result: Accepted 6 Time:3216 ms 7 Memory:8960 kb 8 ****************************************************************/ 9 10 #include <cstdio> 11 #include <vector> 12 #include <algorithm> 13 #include <cstring> 14 using namespace std; 15 struct node 16 { 17 int w; 18 int father; 19 int dep; 20 vector<int> sons; 21 int sum; 22 int maxson; 23 bool vis; 24 int inlink,pos; 25 node(int w,int sum):w(w),sum(sum),vis(0){} 26 }; 27 struct edge 28 { 29 int x,y; 30 edge(int x,int y):x(x),y(y){} 31 }; 32 bool operator <(edge a,edge b) 33 { 34 return (a.x<b.x); 35 } 36 struct segnode 37 { 38 int l,r,lc,rc,max,sum; 39 segnode(int l=0,int r=0,int lc=0,int rc=0):l(l),r(r),lc(lc),rc(rc){} 40 }; 41 struct treelink 42 { 43 int top,tail,len; 44 vector<segnode> segtree; 45 }; 46 int n; 47 vector<edge> edges; 48 vector<node> nodes; 49 void maketree(int now) 50 { 51 nodes[now].vis=1; 52 int s=lower_bound(edges.begin(),edges.end(),edge(now,0))-edges.begin(); 53 int t=upper_bound(edges.begin(),edges.end(),edge(now,0))-edges.begin(); 54 for (int i=s;i<t;i++) 55 { 56 if (!nodes[edges[i].y].vis) 57 { 58 nodes[edges[i].y].father=now; 59 nodes[edges[i].y].dep=nodes[now].dep+1; 60 nodes[now].sons.push_back(edges[i].y); 61 maketree(edges[i].y); 62 } 63 } 64 } 65 int getcount(int now) 66 { 67 nodes[now].sum=1; 68 int lsmax=0; 69 for (unsigned int i=0;i<nodes[now].sons.size();i++) 70 { 71 int t=getcount(nodes[now].sons[i]); 72 nodes[now].sum+=t; 73 if (t>lsmax) 74 { 75 lsmax=t; 76 nodes[now].maxson=nodes[now].sons[i]; 77 } 78 } 79 return nodes[now].sum; 80 } 81 vector<treelink> links; 82 int cnt; 83 void work(int now) 84 { 85 int s=(int)nodes[now].sons.size(); 86 if (!s) 87 return; 88 int x=nodes[now].maxson; 89 nodes[x].inlink=nodes[now].inlink; 90 nodes[x].pos=nodes[now].pos+1; 91 links[nodes[now].inlink].len++; 92 links[nodes[now].inlink].top=x; 93 work(x); 94 for (unsigned int i=0;i<nodes[now].sons.size();i++) 95 { 96 int p=nodes[now].sons[i]; 97 if (p!=x) 98 { 99 cnt++; 100 treelink ls; 101 ls.tail=ls.top=p; 102 ls.len=1; 103 nodes[p].inlink=cnt; 104 nodes[p].pos=1; 105 links.push_back(ls); 106 work(p); 107 } 108 } 109 } 110 vector<int> nodeinlink; 111 vector<int> winlink; 112 int t; 113 int get(int p,int l,int r) 114 { 115 t++; 116 int ls=t; 117 if (l==r) 118 { 119 links[p].segtree[ls]=segnode(l,r,0,0); 120 links[p].segtree[ls].max=links[p].segtree[ls].sum=winlink[l]; 121 return ls; 122 } 123 int mid=(l+r)/2; 124 int lc=get(p,l,mid); 125 int rc=get(p,mid+1,r); 126 links[p].segtree[ls]=segnode(l,r,lc,rc); 127 links[p].segtree[ls].max=max(links[p].segtree[lc].max,links[p].segtree[rc].max); 128 links[p].segtree[ls].sum=links[p].segtree[lc].sum+links[p].segtree[rc].sum; 129 return ls; 130 } 131 void makesegtree(int p) 132 { 133 nodeinlink.clear(); 134 int now=links[p].top; 135 nodeinlink.push_back(now); 136 while (now!=links[p].tail) 137 { 138 now=nodes[now].father; 139 nodeinlink.push_back(now); 140 } 141 winlink.clear(); 142 winlink.push_back(0); 143 for (int i=(int)nodeinlink.size()-1;i>=0;i--) 144 { 145 winlink.push_back(nodes[nodeinlink[i]].w); 146 } 147 t=-1; 148 for (int i=0;i<2*links[p].len+3;i++) 149 links[p].segtree.push_back(segnode()); 150 get(p,1,links[p].len); 151 } 152 void change(int p,int now,int pos,int t) 153 { 154 if (links[p].segtree[now].l>pos || links[p].segtree[now].r<pos) 155 return; 156 if (links[p].segtree[now].l==links[p].segtree[now].r) 157 { 158 links[p].segtree[now].sum=t; 159 links[p].segtree[now].max=t; 160 return; 161 } 162 int lc=links[p].segtree[now].lc; 163 int rc=links[p].segtree[now].rc; 164 change(p,lc,pos,t); 165 change(p,rc,pos,t); 166 links[p].segtree[now].max=max(links[p].segtree[lc].max,links[p].segtree[rc].max); 167 links[p].segtree[now].sum=links[p].segtree[lc].sum+links[p].segtree[rc].sum; 168 } 169 void change(int u,int t) 170 { 171 int p=nodes[u].inlink; 172 int k=nodes[u].pos; 173 change(p,0,k,t); 174 } 175 int getmax(int p,int now,int l,int r) 176 { 177 if (links[p].segtree[now].l>r || links[p].segtree[now].r<l) 178 return -1000000; 179 if (links[p].segtree[now].l>=l && links[p].segtree[now].r<=r) 180 return links[p].segtree[now].max; 181 int maxnow=-1000000; 182 maxnow=max(maxnow,getmax(p,links[p].segtree[now].lc,l,r)); 183 maxnow=max(maxnow,getmax(p,links[p].segtree[now].rc,l,r)); 184 return maxnow; 185 } 186 int qmax(int u,int v) 187 { 188 int p1=nodes[u].inlink; 189 int p2=nodes[v].inlink; 190 int maxnow=-1000000; 191 while (true) 192 { 193 if (p1==p2) 194 return max(maxnow,getmax(p1,0,min(nodes[u].pos,nodes[v].pos),max(nodes[u].pos,nodes[v].pos))); 195 if (nodes[links[p1].tail].dep>=nodes[links[p2].tail].dep) 196 { 197 maxnow=max(maxnow,getmax(p1,0,1,nodes[u].pos)); 198 u=nodes[links[p1].tail].father; 199 p1=nodes[u].inlink; 200 } 201 else 202 { 203 maxnow=max(maxnow,getmax(p2,0,1,nodes[v].pos)); 204 v=nodes[links[p2].tail].father; 205 p2=nodes[v].inlink; 206 } 207 } 208 } 209 int getsum(int p,int now,int l,int r) 210 { 211 if (links[p].segtree[now].l>r || links[p].segtree[now].r<l) 212 return 0; 213 if (links[p].segtree[now].l>=l && links[p].segtree[now].r<=r) 214 return links[p].segtree[now].sum; 215 int sum=0; 216 sum+=getsum(p,links[p].segtree[now].lc,l,r); 217 sum+=getsum(p,links[p].segtree[now].rc,l,r); 218 return sum; 219 } 220 int qsum(int u,int v) 221 { 222 int p1=nodes[u].inlink; 223 int p2=nodes[v].inlink; 224 int sum=0; 225 while (true) 226 { 227 if (p1==p2) 228 return sum+getsum(p1,0,min(nodes[u].pos,nodes[v].pos),max(nodes[u].pos,nodes[v].pos)); 229 if (nodes[links[p1].tail].dep>=nodes[links[p2].tail].dep) 230 { 231 sum+=getsum(p1,0,1,nodes[u].pos); 232 u=nodes[links[p1].tail].father; 233 p1=nodes[u].inlink; 234 } 235 else 236 { 237 sum+=getsum(p2,0,1,nodes[v].pos); 238 v=nodes[links[p2].tail].father; 239 p2=nodes[v].inlink; 240 } 241 } 242 } 243 int main() 244 { 245 scanf("%d",&n); 246 for (int i=1;i<n;i++) 247 { 248 int x,y; 249 scanf("%d%d",&x,&y); 250 edges.push_back(edge(x,y)); 251 edges.push_back(edge(y,x)); 252 } 253 sort(edges.begin(),edges.end()); 254 nodes.push_back(node(0,0)); 255 for (int i=1;i<=n;i++) 256 { 257 int x; 258 scanf("%d",&x); 259 nodes.push_back(node(x,0)); 260 } 261 nodes[1].father=nodes[1].dep=0; 262 maketree(1); 263 getcount(1); 264 treelink ls; 265 ls.tail=ls.top=1; 266 ls.len=1; 267 nodes[1].inlink=0; 268 nodes[1].pos=1; 269 links.push_back(ls); 270 cnt=0; 271 work(1); 272 for (int i=0;i<(int)links.size();i++) 273 makesegtree(i); 274 int q; 275 scanf("%d",&q); 276 for (int i=0;i<q;i++) 277 { 278 char str[10]; 279 scanf("%s",str); 280 if (!strcmp(str,"CHANGE")) 281 { 282 int u,t; 283 scanf("%d%d",&u,&t); 284 change(u,t); 285 } 286 if (!strcmp(str,"QMAX")) 287 { 288 int u,v; 289 scanf("%d%d",&u,&v); 290 printf("%d\n",qmax(u,v)); 291 } 292 if (!strcmp(str,"QSUM")) 293 { 294 int u,v; 295 scanf("%d%d",&u,&v); 296 printf("%d\n",qsum(u,v)); 297 } 298 } 299 return 0; 300 }




