poj1681 Painter's Problem(高斯消元法,染色问题)
题意:
一个n*n 的木板 ,每个格子 都 可以 染成 白色和黄色,( 一旦我们对也个格子染色 ,他的上下左右都将改变颜色);
给定一个初始状态 , 求将 所有的 格子 染成黄色 最少需要染几次? 若 不能 染成 输出 inf。
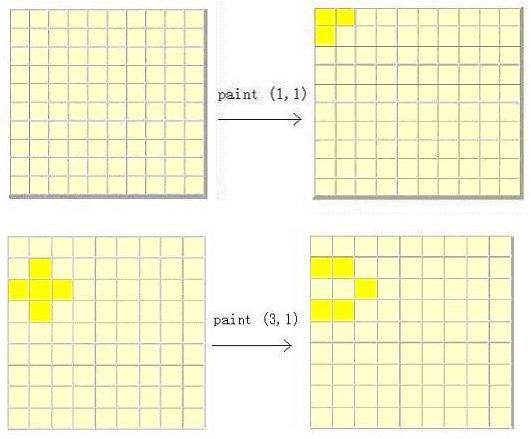
高斯消元,写得很懵逼。慢慢理解orz。
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 #include<cmath> 6 #include<string> 7 #define Inf 0x3fffffff 8 #define maxn 300 9 using namespace std; 10 int n; 11 int a[maxn][maxn]; //增广矩阵 12 int x[maxn]; //解集 13 int free_x[maxn]; //标记是否为不确定的变元 14 void init(){ 15 memset(a,0,sizeof(a)); 16 memset(x,0,sizeof(x)); 17 memset(free_x,1,sizeof(free_x)); 18 for (int i=0;i<n;i++){ 19 for (int j=0;j<n;j++){ 20 int t=i*n+j; 21 a[t][t]=1; 22 if (i>0) a[(i-1)*n+j][t]=1; 23 if (i<n-1) a[(i+1)*n+j][t]=1; 24 if (j>0) a[i*n+j-1][t]=1; 25 if (j<n-1) a[i*n+j+1][t]=1; 26 } 27 } 28 } 29 // 高斯消元法解方程组(Gauss-Jordan elimination).(-2表示有浮点数解,但无整数解, 30 //-1表示无解,0表示唯一解,大于0表示无穷解,并返回自由变元的个数) 31 //有equ个方程,var个变元。增广矩阵行数为equ,分别为0到equ-1,列数为var+1,分别为0到var. 32 int Gauss(int equ,int var){ 33 for (int i=0;i<=var;i++){ 34 x[i]=0; 35 free_x[i]=0; 36 } 37 int i,j,k,num=0; 38 int now=0;//当前处理的列 39 for (k=0;k<equ && now<var;k++,now++){ //枚举行 40 int max_r=k; 41 for (i=k+1;i<equ;i++){ 42 if (abs(a[i][now])>abs(a[max_r][now])) max_r=i; 43 } 44 if (max_r!=k){//与第i行交换 45 for (j=k;j<=var;j++) swap(a[k][j],a[max_r][j]); 46 } 47 if (a[k][now]==0){// 说明该now列第k行以下全是0了,则处理当前行的下一列. 48 k--; 49 free_x[num++]=now; 50 continue; 51 } 52 for (i=k+1;i<equ;i++){ 53 if (a[i][now]!=0){ 54 for (j=now;j<=var;j++){ 55 a[i][j]^=a[k][j]; 56 } 57 } 58 } 59 } 60 // 1. 无解的情况: 化简的增广阵中存在(0, 0, ..., a)这样的行(a != 0). 61 for (i=k;i<equ;i++){ 62 // 对于无穷解来说,如果要判断哪些是自由变元,那么初等行变换中的交换就会影响,则要记录交换. 63 if (a[i][now]!=0) return -1; 64 } 65 int stat=1<<(var-k); //自由变元有 var-k 个 66 int res=Inf; 67 for (i=0;i<stat;i++){ //枚举所有变元 68 int cnt=0,index=i; 69 for (j=0;j<var-k;j++){ 70 x[free_x[j]]=(index&1); 71 if (x[free_x[j]]) cnt++; 72 index>>=1; 73 } 74 for (j=k-1;j>=0;j--){ 75 int tmp=a[j][var]; 76 for (int l=j+1;l<var;l++){ 77 if (a[j][l]) tmp^=x[l]; 78 } 79 x[j]=tmp; 80 if (x[j]) cnt++; 81 } 82 if (cnt<res) res=cnt; 83 } 84 return res; 85 } 86 int main(){ 87 int t; 88 cin >> t; 89 string str; 90 while (t--){ 91 cin >> n; 92 init(); 93 for (int i=0;i<n;i++){ 94 cin >> str; 95 for (int j=0;j<n;j++){ 96 if (str[j]=='y') a[i*n+j][n*n]=0; 97 else a[i*n+j][n*n]=1; 98 } 99 } 100 int k=Gauss(n*n,n*n); 101 if (k==-1) cout << "inf\n"; 102 else cout << k << endl; 103 } 104 return 0; 105 }



