zoj3497 Mistwald（矩阵快速幂）

题意：给定一个有向图（最多25个节点，每个节点的出度最多为4），给定起点和终点，然后从起点开始走，走到终点就停止，否则一直往下走，问能不能P步到达终点。也就是说从起点出发，走一条长度为P的路径，路径中间点不能经过终点（但可以反复经过其他点）。如果从起点出发P步后，不能到达终点，就是False，如果可以到达终点也可以到其他别的点，就是Maybe，如果P步后只能到达终点（到别的点没有长度为P的路径），则是Yes。

 

样例输入意思：四个坐标分别为，m*n矩阵中的坐标，通过次计算出每个节点对应的出口，然后建图。

 

分析：图的邻接矩阵A的 p次方A^p中为1的元素(i,j)表示节点i到节点j有一条长度为p的路径（经历的节点可能重复）。要理解矩阵的含义，两个矩阵相乘如果(x,y)元素为1，而(y,z)元素为1,则结果(x,z)元素为1，这表明通过y把x和z连起来了。而题目要求经过终点就不能走了，所以在做矩阵乘法时，需要把（x,n-1） (n-1,y)这样决定的(x,y)去掉。（n-1表示终点）。做乘法时，中间点小心一点就好了。矩阵乘法和floyd在本质上是一样的……

Orz..矩阵乘法还可以写成松弛操作。（是我辣鸡了）

 

 

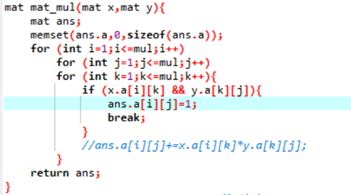
矩阵的P次方运用的是经典的log(P)的算法。最后看一下结果矩阵的首行（0行）里面有几个1，以及(0,n-1)是不是1，来决定结果。

#include<iostream>
#include<cstdio> 
#include<cstring>
#define maxn 30
using namespace std;
struct mat{
    int a[maxn][maxn];
};
mat map;
int mul;
mat mat_mul(mat x,mat y){
    mat ans;
    memset(ans.a,0,sizeof(ans.a));
    for (int i=1;i<=mul;i++)
        for (int j=1;j<=mul;j++)
        for (int k=1;k<=mul;k++){
            ans.a[i][j]+=x.a[i][k]*y.a[k][j];
        }
    return ans;
}
mat mat_pow(mat map,int k){ //map的k次方 
    mat c=map,res=map;
    k--;
    while (k){
        if (k&1) res=mat_mul(res,c);
        k>>=1;
        c=mat_mul(c,c);
    }
    return res;
}
int main(){
    int t,m,n,q;char ch;
    int xx;
    int x[5],y[5];
    scanf("%d",&t);
    while (t--){
        scanf("%d%d",&m,&n);scanf("%c",&ch);
        mul=m*n;
        memset(map.a,0,sizeof(map.a));
        for (int i=1;i<=m;i++){
            for (int j=1;j<=n;j++){
                scanf("((%d,%d),(%d,%d),(%d,%d),(%d,%d))",&x[0],&y[0],&x[1],&y[1],&x[2],&y[2],&x[3],&y[3]);
                scanf("%c",&ch);
                if (i==m && j==n) continue; //途中路径不能经过终点
                for (int k=0;k<4;k++){
                    map.a[(i-1)*n+j][(x[k]-1)*n+y[k]]=1;
                }
            }
        }
        scanf("%d",&q);
        while (q--){
            scanf("%d",&xx);
            mat S;
            if (xx) S=mat_pow(map,xx);
            else {
                memset(S.a,0,sizeof(S.a));
                for (int i=0;i<=mul;i++) S.a[i][i]=1;
            }
            if (!S.a[1][mul]) printf("False\n");
            else {
                int flag=0;
                for (int i=1;i<mul;i++){
                    if (S.a[1][i]){
                        flag=1;
                        break;
                    }
                }
                if (flag) printf("Maybe\n");
                else printf("True\n");
            }
        }
        printf("\n");
    }
    return 0;
}

PS.迷之TLE无数发。各种迷。最后是因为快速幂姿势和别人有所不同，矩阵的0次方需要特判赋值为单位矩阵。orz....太菜了。