十大排序算法-------【归并排序】详解(Java源码)
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法的一个非常典型的应用。将已经有序的子序列合并,得到完全有序的序列;即先使得每个子序列有序,再使得子序列之间有序。若将两个有序表合并成一个有序表,称为2-路归并。
- 算法描述:
- 把长度为n的输入序列分成两个长度为n/2的子序列
- 对这两个子序列分别采用归并排序
- 将两个排序好的子序列合并成一个最终的排序序列。

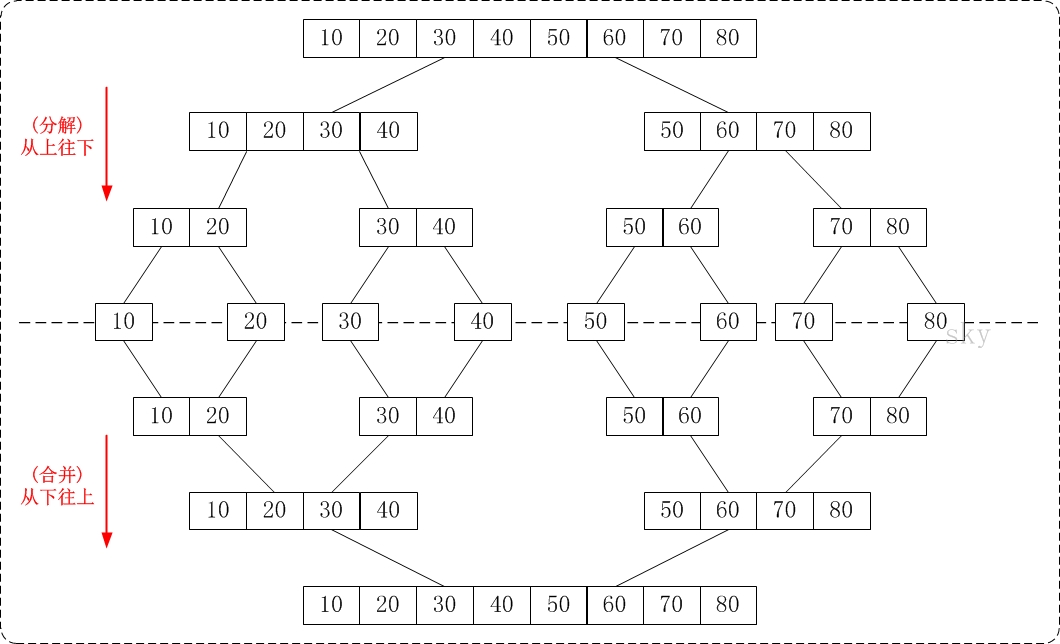
- 代码:
private static void guibing(int[] intArray) {
int[] intArrayTemp = new int[intArray.length];// 此处是为了减少递归中频繁创建int数组
guibing(intArray, 0, intArray.length - 1, intArrayTemp);
}
private static void guibing(int[] intArray, int left, int right, int[] intArrayTemp) {
if (left < right) {
int mid = (left + right) / 2;
guibing(intArray, left, mid, intArrayTemp);
guibing(intArray, mid + 1, right, intArrayTemp);
// 对该序列进行合并
hebing(intArray, left, mid, right, intArrayTemp);
}
}
private static void hebing(int[] intArray, int left, int mid, int right, int[] intArrayTemp) {
int i1 = left, i2 = mid + 1;
int t = 0;
while (i1 <= mid && i2 <= right) {
if (intArray[i1] <= intArray[i2]) {
intArrayTemp[t++] = intArray[i1++];
} else {
intArrayTemp[t++] = intArray[i2++];
}
}
while (i1 <= mid) {
intArrayTemp[t++] = intArray[i1++];
}
while (i2 <= right) {
intArrayTemp[t++] = intArray[i2++];
}
t = 0;
while (left <= right) {// 关键一步
intArray[left++] = intArrayTemp[t++];
}
}
- 算法分析,归并排序是一种稳定的排序方法(其实我个人不觉得是一定稳定的)。和选择排序一样,归并排序的性能不受需排序的数据的影响,但是表现比选择排序好,因为其时间复杂度始终是O(nlogn)的。代价就是需要开辟临时内存空间。
- 个人看法:归并排序相较选择排序来说,我个人认为在归并排序中是包含了选择排序的算法理论的。归并排序其主要是靠分治思想,通过递归实现将总序列一分为二,二分为四,四分为八…通过递归实现。然后在分割的底部其单个子序列长度为2,3,那么将对子序列实现选择排序,将对应相邻的两个子序列遍历比较其元素内容大小,然后通过临时序列接收,然后将临时序列替换子序列所有内容。最终,递归顶部实现最大的两个子序列拼接。反馈排序后的序列。



