图像特征提取：HOG、LBP、Haar特征

1、图像特征

特征是某一类对象区别于其他类对象的相应（本质）特点或特性，或是这些特点和特性的集合。特征是通过测量或处理能够抽取的数据。对于图像而言，每一幅图像都具有能够区别于其他类图像的自身特征，有些是可以直观地感受到的自然特征，如亮度、边缘、纹理和色彩等；有些则是需要通过变换或处理才能得到的，如矩、直方图以及主成份等。

2、图像处理

图像处理中最常用到的三种特征：Haar特征、LBP特征及HOG特征分别描述了三种不同的局部信息：

1) Haar描述的是图像在局部范围内像素值明暗变换信息；

2) LBP描述的是图像在局部范围内对应的纹理信息；

3) HOG描述的则是图像在局部范围内对应的形状边缘梯度信息。

2.1、Haar特征

最容易接触到Haar特征地方应该就是opencv自带的人脸检测器，所采用的就是Haar特征结合Adaboost算法来实现的，利用Haar特征表征人脸在局部范围内像素值的明暗变化信息，结合积分图技巧加速训练一个级联的Adaboost分类器。Haar特征表示如图1所示：

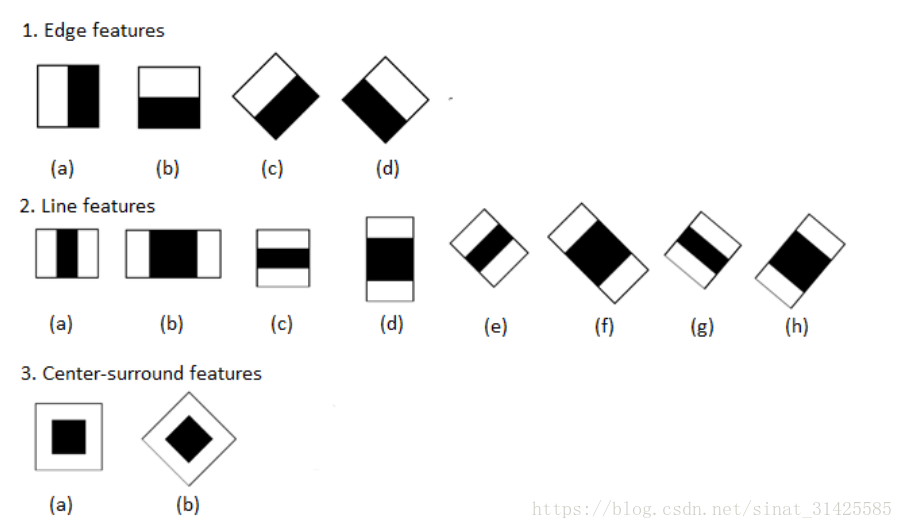
图 1 Haar特征

计算过程就是黑色矩形区域内像素值之和减去白色矩形区域内像素值之和，计算过程其实很简单。但是，直接计算的话，针对每一个矩形区域，我们都需要做一次循环，计算区域内像素之和，对每个位置进行滑窗遍历进行Haar特征提取会使得计算量爆炸，因此，一般Haar特征会配合积分图技术一起来使用。

积分图计算如图2所示，经过计算后，积分图中每个点对应值Inter(x,y)为对应蓝色矩形区域像素值之和。

图 2 积分图

当需要提取Haar特征时，我们需要计算矩形块中像素值之和时，我们只需要将其四个顶点对应于积分图中的值拿出来，做一个求和操作即可，计算过程如图3所示。

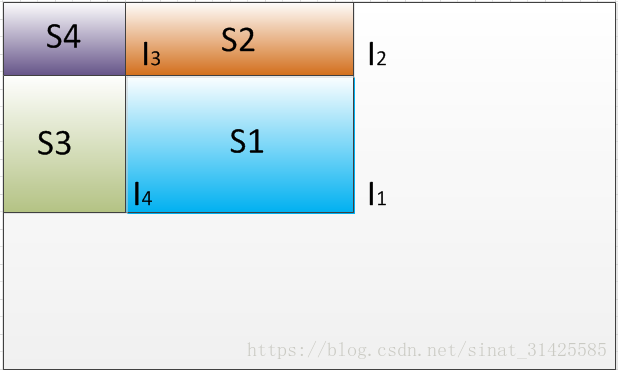
S1的面积等与I₁-I₂-I₄+I₃，一个矩形区域内像素累加求和计算转变成了几个值的加减运算，大大的提升了算法执行效率。

2.2、LBP特征

Local Binary Pattern（局部二进制模式）简称，LBP特征对于传统的人脸识别而言，应该是十分有效的。LBP特征提取的思路就是，图像中某一个物体应该包含有多个像素，而且像素与像素之间位置关系应该是连续的，也即是说，在空间位置上有关联的像素信息也是有关联的，因此，可以考虑利用在空间位置上邻近的像素来对当前像素进行二进制编码，这也就是LBP。

常见的LBP有LBP，CS-LBP，Uniform-LBP，圆形LBP和旋转不变LBP等。LBP、CS-LBP和Uniform-LBP都是基于当前像素的八邻域来计算的，八邻域示意图如图4所示：

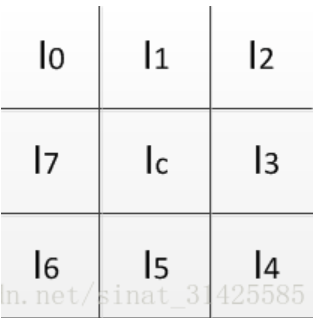
图 4 8领域示意图

传统LBP计算公式：

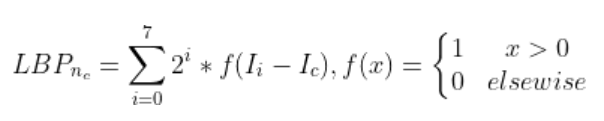
然而原始的LBP存在以下几个问题：

1) 固定邻域内的编码，对于尺度比较敏感，例如，人脸尺寸发生变化，人脸编码会出现误差；

2) LBP特征的维度为 $2^{8}=256$ 维，特征维度过高；

3）对于光照、旋转等因素敏感。

针对上述问题，CS-LBP利用中心对称的思想对局部纹理进行描述，其计算公式为：

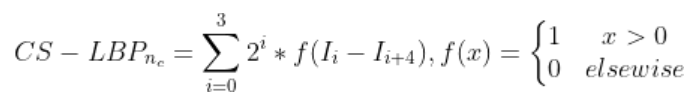
CS-LBP特征的维度为维，相较于传统的LBP，大大地降低了特征维度，大大提升了计算效率。同时，这种对称计算的方式，能够在一定程度上应对光照、旋转等因素。Uniform-LBP翻译过来可以是等价模式，作者Ojala的灵感来自于，通过大量实验发现：在实际图像中，绝大多数LBP模式最多只包含两次从1到0或从0到1的跳变，因此，在实际应用中，我们只需要统计那些跳变次数在[0,2]之间的二进制模式（这些LBP也称之为等价模式，即Uniform-LBP），经过统计发现，满足这样的LBP总共只有58种，这样，256维的LBP就变成了58维的Uniform-LBP了。

圆形LBP采用圆形邻域取代3方形邻域，并且可以通过调整半径，将3x3大小领域扩展到任意大小邻域。圆形LBP可以在一定程度上缓解尺度因素引起的变化，但是对于旋转因素较为敏感，因此，在圆形LBP的基础上，研究者提出了旋转不变LBP。旋转不变LBP对应旋转不变指的是，将圆形领域进行旋转LBP编码，将最小的LBP编码值作为当前像素点的编码值，这样，当物体发生旋转时，能够提取到的LBP编码值具备一定的旋转不变性。

2.3、HOG特征

Histogram of Gradient(梯度直方图)缩写，主要应用于图像中的边缘检测，主要步骤如下：

转为灰度图；
gamma变换：降低局部阴影和光照变化影响；
梯度计算：利用一阶或二阶差分近似计算图像梯度及方向：

梯度分量计算：

梯度和方向计算：

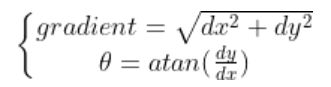
4. 方向划分：将方向对应角度区间离散化及模糊处理

首先，将方向对应角度无符号化，其实本质上就是将位于一条直线上的两个方向都视为一个角度，也即是 $\theta$ 与 $\theta-\pi$ 视为同一个角度，其中 $\theta>0$ ，这样方向范围就变成了 $[0,\pi]$ ；然后，将角度范围均等划分为9个bins，每一个bin对应一个角度，所有bins对应的角度为： $[0,\pi /9,2\pi /9,3\pi /9,...,8\pi /9]$

5. 梯度直方图统计：

通过每个像素的梯度值和梯度方向做梯度直方图统计，如图5所示

图 5 梯度直方图计算示意图

如果梯度方向正好位于bins的边界线上时，将对应梯度值加到bins中，图5中的梯度值2对应的梯度方向正好在bins 80边界上，则把2直接加到bins 80中，如果梯度值不是正好位于边界上，使用插值的方式进行分配，假设梯度grad位于bins[i]和bins[i+1]分界线之间，则加入bins[i]的梯度值为：grad*(grad-bins[i])/20，加入bins[i+1]的梯度值为：grad*(bins[i+1]-grad)/20。

而单个像素的梯度对于噪声比较敏感，直接对每一个像素梯度进行统计，得到的特征可能不够鲁棒，因此，将图像进行分块统计，HOG原文是将图像划分为8x8大小的cell，cell的个数为：