自动微分
0、前言
现在深度学习流行的框架训练模型的思想都是通过通过前向计算得到损失函数,再通过反向传播通过损失函数对权重反向求导更新权重,将目标函数(损失函数)达到一个最小的值。目前存在的反向求导方法:
- 手动微分
- 数值微分
- 符号微分
- 自动微分
各个深度学习框架最核心也是最重要的核心就是如何进行自动微分(基于计算图)。正因为自动微分的存在,才使得深度学习框架可以根据我们设定的损失函数实现最重要的梯度更新操作。自动微分和BP最主要的区别是,自动求导没有提前计算出每个算子的导数,仅仅是将计算式子表达出来而已,直到我们确实需要求这个值的时候,整个计算流程才算开始执行。这是一种延迟计算的思想,我们将所有要计算的路线都规划好之后再进行计算,这样一是可以不用提前计算出中间变量,二是可以根据我们导出的计算节点的拓扑关系进行一些优化之类的工作,总的来说比较灵活。
1、实现自动微分Autodiff算法
1.1、算法基本流程
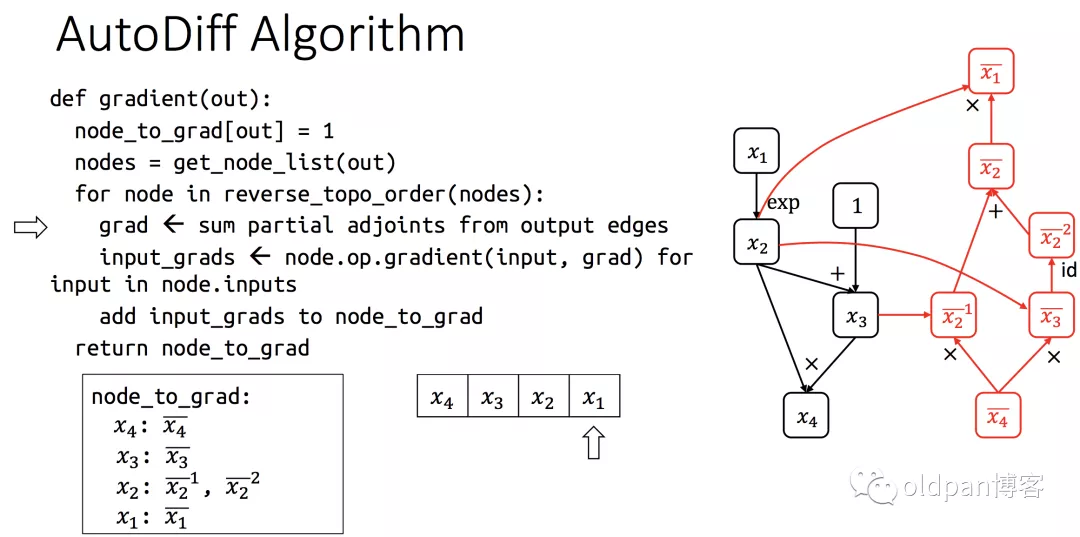
我们根据目标函数f=(ex +1)ex去求每个变量x1,x2,x3,x4的导数。相应的伪代码如下:

这里我们是逆序推导的方式,也就是从输出端一直推导到输入端,而每一个节点都称之为node,例如x4=x2*x3 ,这时x4就相当于一个node,要注意这个node与这个节点的op也有关系,比如这个的op就是mul也就是乘法。
然后我们计算输出的导数(其实就是x4的导数),显然是1,因为x4就是输出么,这里的node_to_grad储存的是每个node对应的导数。

然后我们走到了第一个节点x4,我们接着往上走,准备去求x4两个输入的导数(x2,x3),再提醒一下,这里是逆序。依次对几个变量逆序求导得到每个node的导数
1.2、相关代码
Node是每个计算节点,之后的每个具体的node都要去继承这个类。这个类重载了加法和乘法操作。


