(抄自己luogu上的博客)莫队总结
虽然当时文风很2,但是觉得写的蛮好的,就在这里贴一下吧。
最近学了分块(太难想了 \(qwq\) )和莫队(太神奇了 \(0w0\) ),写一个阶段性总结~
分块
总所周知,分块是一种神奇的暴力,用 \(O(n\sqrt{n})\) 的较为优秀的时间复杂度,解决线段树与树状数组不能解决之事
那么,他是怎么做到的呢?
我们找一道模版题:
请问线段树和树状数组,您二位又该如何应对?
用线段树?_ Sunmoon _表示,所有线段树做法都可以被题目最后新增的那组hack干掉!
那怎么办?
这时,我们的分块闪亮登场! \(0w0\)
假如树状数组是一颗神奇的树,线段树是一颗高度为 \(log_2n\) 的神奇的树,那分块所产生的块状数组,就是一颗高度仅为3层的神奇的树,如下图:
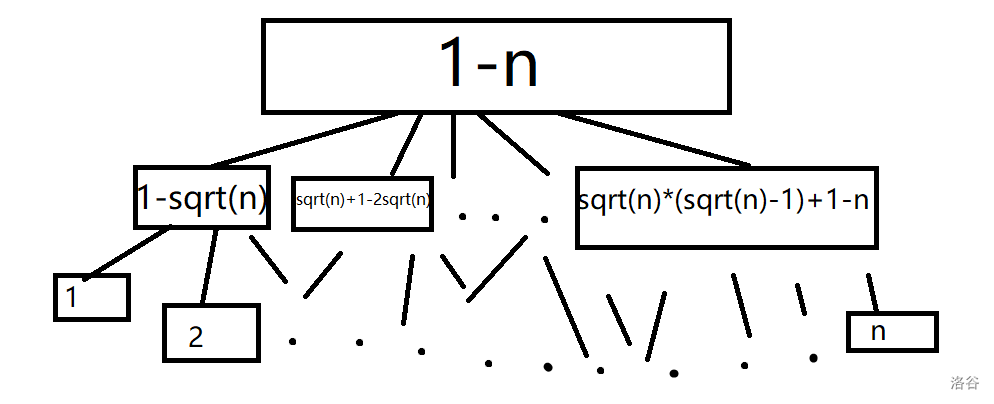
第一层,他的块长为 \(n\)
第二层,他的块长为 \(\sqrt{n}\)
第三层,对标到每个元素
那么,块分好了,该如何在块上操作呢?
妈妈我会分段!
考虑分成三个部分:

对于两个散块部分,进行修改的时间复杂度不超过 \(O(\sqrt{n})\)
对于一个整块部分,直接将所加的值给整块部分即可,时间复杂度 \(O(\sqrt n)\)
于是,我们支持了 \(O(\sqrt{n})\) 的修改操作(当然这种思路也可以用来做树状数组和线段树的模版题)
那么,如何查询呢?
还是分成原来三个部分
对于两个散块部分,直接暴力看有没有超过c,时间复杂度 \(O(\sqrt n)\)
对于中间的整块部分,我们可以将其提前排序,在查找时二分,时间复杂度 \(O(\sqrt n\ log_2 \sqrt n)\),提前排序时间复杂度为 \(O(nlog_2\sqrt n)\)
所以时间复杂度为 \(O(max(q\sqrt n\ log_2\sqrt n\ ,nlog_2\sqrt n))\),稳稳AC
这就是分块可怕的威力
贴代码~
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,q,l,c[1000005],add[1005];
int k[1005][1005],z[1005][1005],h[1005][1005];
struct zjy{int a,b;}lyh[1005];
int cmp(zjy x,zjy y){return x.a<y.a;}
void sk(int kk,int r){
for(int i=1;i<=r;i++){
lyh[h[kk][i]].a=k[kk][i];
lyh[h[kk][i]].b=h[kk][i];
}
sort(lyh+1,lyh+r+1,cmp);
for(int i=1;i<=r;i++){
k[kk][i]=lyh[i].a;
z[kk][lyh[i].b]=i;
h[kk][i]=lyh[i].b;
}
}
void liu(){
int x,y,w;cin>>x>>y>>w;
int k1=(x-1)/l+2,k2=(y-1)/l;
int k3=(x-1)/l+1,k4=(y-1)/l+1;
if(k3==k4){
for(int i=((x%l)?x%l:l);i<=((y%l)?y%l:l);i++)
k[k3][z[k3][i]]+=w;
sk(k3,(k3>n/l)?n%l:l);return;
}
for(int i=((x%l)?x%l:l);i<=l;i++)
k[k3][z[k3][i]]+=w;
for(int i=1;i<=((y%l)?y%l:l);i++)
k[k4][z[k4][i]]+=w;
sk(k3,l);sk(k4,(k4>n/l)?n%l:l);
for(int i=k1;i<=k2;i++) add[i]+=w;
}
void zhang(){
int x,y,w;cin>>x>>y>>w;
int k1=(x-1)/l+2,k2=(y-1)/l;
int k3=(x-1)/l+1,k4=(y-1)/l+1;
int ans=0;
if(k3==k4){
for(int i=((x%l)?x%l:l);i<=((y%l)?y%l:l);i++)
if(k[k3][z[k3][i]]+add[k3]>=w) ans++;
cout<<ans<<"\n";return;
}
for(int i=((x%l)?x%l:l);i<=l;i++)
if(k[k3][z[k3][i]]+add[k3]>=w) ans++;
for(int i=1;i<=((y%l)?y%l:l);i++)
if(k[k4][z[k4][i]]+add[k4]>=w) ans++;
for(int i=k1;i<=k2;i++){
int d=lower_bound(k[i]+1,k[i]+l+1,w-add[i])-k[i];
ans+=l-d+1;
}
cout<<ans<<"\n";
}
signed main(){
cin>>n>>q;l=sqrt(n);
for(int i=1;i<=n;i++) cin>>c[i];
for(int s=1,e=l;s<=n;s+=l,e=min(e+l,n)){
for(int i=1,j=s;j<=e;i++,j++)
lyh[i].a=c[j],lyh[i].b=i;
sort(lyh+1,lyh+e-s+2,cmp);
for(int i=1;i<=e-s+1;i++){
k[(s-1)/l+1][i]=lyh[i].a;
z[(s-1)/l+1][lyh[i].b]=i;
h[(s-1)/l+1][i]=lyh[i].b;
}
}
while(q--){
char c;cin>>c;
if(c=='M') liu();
else zhang();
}
return 0;
}
事实证明,分块威力远不止于此
首先,我们有一个暴力的思路:
记录每个点弹到的下一个点,询问时递推暴跳即可
我们发现,假如按常规思路,这题是绝对做不出来的
那么,分块就成为了一个很好的办法
我们记录两个东西:
1、弹出自己所在的块后到达的第一个点
2、弹出自己所在的块所需的步数
预处理时,可以递推 \(O(n)\) 记录
修改时,只需要修改块内的元素,时间复杂度 \(O(\sqrt n)\)
暴跳顶多调块数次,时间复杂度 \(O(\sqrt n)\)
综上,时间复杂度为 \(O(max(n,m\sqrt n))\)
参考代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,q,l,k[200005];
int nxt[200005],b[200005];
signed main(){
cin>>n;l=sqrt(n);
for(int i=0;i<n;i++) cin>>k[i];
for(int i=n-1;i>-1;i--){
if((i+k[i])/l!=i/l||i+k[i]>=n)
b[i]=1,nxt[i]=i+k[i];
else b[i]=b[i+k[i]]+1,nxt[i]=nxt[i+k[i]];
}
cin>>q;
while(q--){
int o,x,c;cin>>o>>x;
if(o==1){
int ans=0;
while(x<n) ans+=b[x],x=nxt[x];
cout<<ans+b[x]<<"\n";continue;
}
cin>>c;k[x]=c;
for(int i=x;i>=x/l*l;i--){
if((i+k[i])/l!=i/l||i+k[i]>=n)
b[i]=1,nxt[i]=i+k[i];
else b[i]=b[i+k[i]]+1,nxt[i]=nxt[i+k[i]];
}
}
return 0;
}
//怎么说呢……就挺短吧……
至此,我们就了解了分块算法
莫队
莫队,是由前国家队队长莫涛神犇总结出的一种以分块思想优化排序的离线做法
考虑这个问题
很明显,我们可以对于每个区间,直接 \(O(n^2)\) 暴力
虽说《n方过百万》,但是这看起来也不是个啥好想法
我们有了一种新的想法!
建立两个指针,在数轴上乱跳!如下图:
从这样的状态

变成这样的状态

虽然时间复杂度没有直接优化,但是为我们下一步理解莫队算法打下基础
考虑充分利用可以离线的性质:
将所有询问离线下来,并且以L为关键字排序,这个时候再跳,常数很明显变小了(因为L最多只会跳n下)
可时间复杂度还是没变(R会反复横跳)……
陆游说得好,“山重水复疑无路,柳暗花明又一村”,这时,莫涛神犇为广大OI选手带来了一线曙光。他告诉我们:只要按照分块的思路排序,时间复杂度就可以达到最坏 \(O(n\sqrt n)\)!于是,普通莫队算法诞生了!(我在说啥?)
排序cmp的变化:
int cmp(zjy x,zjy y){
//原来
if(x.l!=y.l) return x.l<y.l;
return x.r<y.r;
//现在
if(x.l/len!=y.l/len) return x.l<y.l;
return x.r<y.r;
}
那么,为什么他的时间复杂度为 \(O(n\sqrt n)\) 呢?
为使过程看起来一目了然,我在描述时可能不会很精确,想要看精准证明,请移步这里
下面开始证明:
考虑在每个块中,R最多跳n次,时间复杂度 \(O(n\sqrt n)\)
L每次跳的量不会超过 \(\sqrt n\) 级别,时间复杂度 \(O(q\sqrt n)\)
当然,这里将询问次数与数列长度视为同阶的。假如两者差异过大,那就要仔细考虑
于是,我们就可以完成对普通莫队算法的逻辑梳理了!
1、排序 2、指针暴跳求答案 3、完结撒花
于是代码就有啦
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m,k,b[50005],l=1,r,a,ans;
int p[50005],c[50005],re[50005];
struct zjy{
int s,e,id;
bool operator<(const zjy &x)const{
if(s/a!=x.s/a) return s<x.s;
if(s/a%2) return e<x.e;
return e>x.e;
}
}q[50005];
void add(int x){ans-=c[b[x]]*c[b[x]]-(c[b[x]]+1)*(c[b[x]]+1);c[b[x]]++;}
void del(int x){ans-=c[b[x]]*c[b[x]]-(c[b[x]]-1)*(c[b[x]]-1);c[b[x]]--;}
signed main(){
cin>>n>>m>>k;a=sqrt(n);
for(int i=1;i<=n;i++) cin>>b[i];
for(int i=1;i<=m;i++){
cin>>q[i].s>>q[i].e;
q[i].id=i;
}
sort(q+1,q+m+1);
for(int i=1;i<=m;i++){
while(r<q[i].e) add(++r);
while(r>q[i].e) del(r--);
while(l<q[i].s) del(l++);
while(l>q[i].s) add(--l);
re[q[i].id]=ans;
}
for(int i=1;i<=m;i++) cout<<re[i]<<"\n";
return 0;
}
部分 \(dalao\) 可能会发现一个很重要的问题:本蒟蒻的排序函数变了!
这是为什么呢?
实际上,这是一个略微玄学的优化:奇偶化排序
什么意思呢?
假如按照原来的排序函数,在跳R的时候,每次都要先往右跳,然后一个大跳跳回来,再继续往右跳,但假如我们在R回来的时候,就解决了下一个块的询问,岂不美哉?
于是,我们选择在奇数块向右跳,在偶数块时再向左跳回来。根据某 \(dalao\) 的研究,奇偶化排序通常可以减少30%的时间
那我们再来看下一道题:
哪里来的修改?莫队,请问您的修改操作呢?
好吧,如此优雅的暴力很明显也有了致命的缺点:你怎么修改?
有没有暴力一点的解决方式呢?
有!
我们发现,我们刚刚研究的莫队只是在一维上的,我们可否再加一维时间维?
答案是肯定的。我们可以将时间指针T作为排序的第三关键字
假如我们的T小于现在所枚举的时间,我们就让他顺流而上;假如大于,则顺流而下(可以发现,在向上枚举时,原来被修改位置上的数字和修改后的数字地位交换)
那么代码就不难敲了
#include<bits/stdc++.h>
using namespace std;
int w,tms[2][200005],a;
int n,m,k,b[200005],ans;
int c[1000005],re[200005];
struct zjy{
int s,e,t,id;
bool operator<(zjy x){
if(s/a!=x.s/a) return s<x.s;
if(e/a!=x.e/a) return e<x.e;
return t<x.t;
}
}q[200005];//我知道但是zjy永远滴神
void add(int x){if(!c[x]) ans++;c[x]++;}
void del(int x){c[x]--;if(!c[x]) ans--;}
signed main(){
cin>>n>>m;a=(int)pow(n,2.0/3.0);
for(int i=1;i<=n;i++) cin>>b[i];
for(int i=1;i<=m;i++){
char o;int ll,rr;
cin>>o>>ll>>rr;
if(o=='Q') q[++k]={ll,rr,w,k};
else{tms[0][++w]=ll;tms[1][w]=rr;}
}
// sort(q+1,q+k+1);
int l=1,r=0,tt=0;
for(int i=1;i<=k;i++){
while(r<q[i].e) add(b[++r]);
while(r>q[i].e) del(b[r--]);
while(l<q[i].s) del(b[l++]);
while(l>q[i].s) add(b[--l]);
while(tt<q[i].t){
++tt;
if(l<=tms[0][tt]&&tms[0][tt]<=r)
del(b[tms[0][tt]]),add(tms[1][tt]);
swap(b[tms[0][tt]],tms[1][tt]);
}
while(tt<q[i].t){
if(l<=tms[0][tt]&&tms[0][tt]<=r)
del(b[tms[0][tt]]),add(tms[1][tt]);
swap(b[tms[0][tt]],tms[1][tt]);--tt;
}
re[q[i].id]=ans;
}
for(int i=1;i<=k;i++) cout<<re[i]<<"\n";
return 0;
}
虽然代码长了不少,但是基本思路没有变
莫队还有树上莫队等其他分支类型,我会在学明白之后再写一篇详解
感谢您的观看,希望您不要吝惜您的点赞


