神经网络模型及前向传播算法算法推导

神经网络介绍

T. Kohonen于1988年在Neural Networks创刊号上给出了神经网络的定义：神经网络是由具有适应性的简单单元组成的广泛并互连的网络，它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。

神经网络中最基本的成分是神经元（neuron）模型（即上述定义中的“简单单元”），包括感知机、Sigmoid函数等。把许多个这样的神经元按一定的层次结构连接起来，就得到了神经网络。

神经网络是感知机的拓展。与感知机相比，神经网络1）输入层和输出层之间包含了隐含层（hidden layer），隐含层和输出层神经元都是拥有激活函数的功能神经元；2）激活函数不局限于$sign(x)$函数；3）输出层的神经元可以有多个；4）基于线性拟合，通过激活函数引入非线性因素，可用于解决非线性可分问题。

神经网络结构

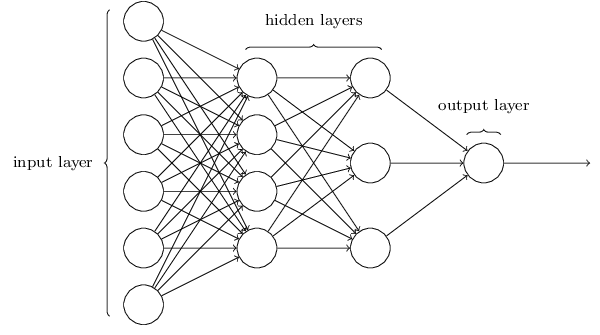
每层神经元与下一层神经元全互连，神经元之间不存在同层连接，也不存在跨层连接，这样的神经网络结构称为“前馈神经网络”（ feedforward neural network） 。也就是说，在前馈神经网络中，将上一层的输出用作下一层的输入，信息总是向前流动。有时被称为多层感知机（ multilayer perceptron, MLP），尽管它是由 Sigmoid神经元而不是感知机组成的。当然，还有其他人工神经网络模型，如递归神经网络模型，但前馈神经网络是应用最广泛的。

神经网络前向传播算法算法推导

如图所示为含有3个输入单元、3个隐含单元和一个输出单元的前馈神经网络：

 

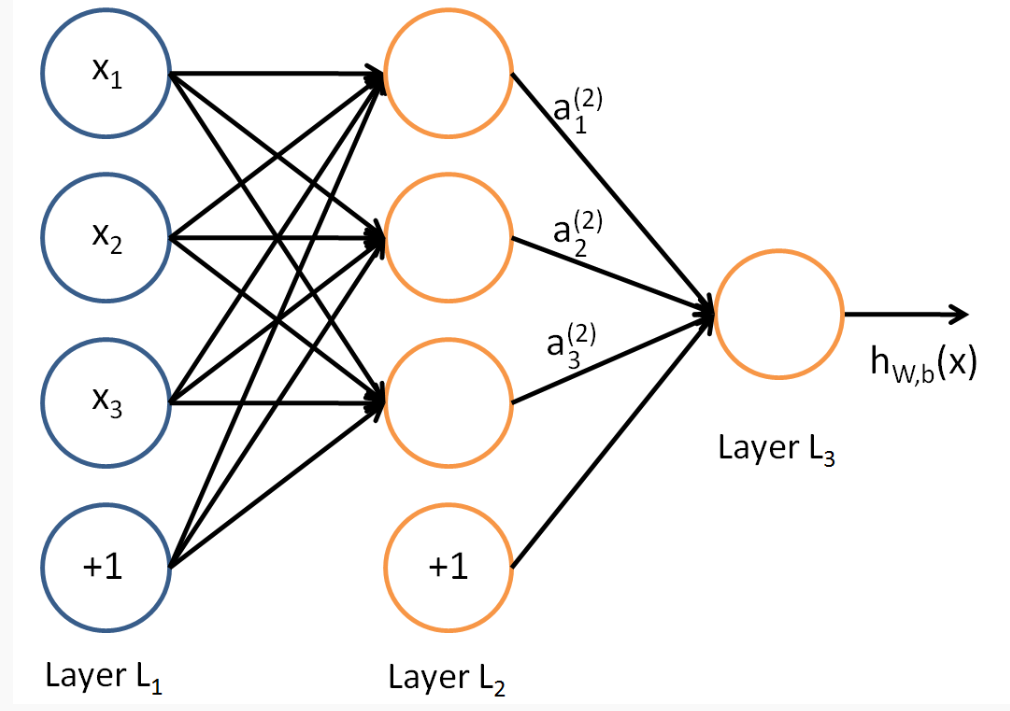
最左边Layer L₁表示输入层，最右边Layer L₃表示输出层，中间Layer L₂表示隐藏层。其中，圆圈中的"+1"表示偏差项，也就是截距项。$n_l$表示神经网络的层数，此处为3；将第$l$层标记为$L_l$，则输出层为$L_{nl}$。$w^{(l)}_{ij}$表示第$l$层第$j$个神经元到第$l+1$层的第$i$个神经元的权重参数。$b^{(l)}_i$表示第$l+1$层第$i$个神经元的偏差项。$a^{(l)}_i$表示第$l$层的第$i$个神经元的输出。

代数法求解

当$l=1$时，$a^{(1)}_i=x_i$；

$a^{(2)}_1=f(w^{(1)}_{11}x_1+w^{(1)}_{12}x_2+w^{(1)}_{13}x_3+b^{(1)}_1)$

$a^{(2)}_3=f(w^{(1)}_{31}x_1+w^{(1)}_{32}x_2+w^{(1)}_{33}x_3+b^{(1)}_3)$

$a^{(3)}_1=f(w^{(2)}_{11}a^{(2)}_1+w^{(2)}_{12}a^{(2)}_2+w^{(2)}_{13}a^{(1)}_3+b^{(2)}_1)$

令$a^{(l)}_i=f(z^{(l)}_i)$，则$z^{(l)}_i=\sum\limits_{j=1}^n w^{(l-1)}_{ij}a^{(l-1)}_j+b^{(l-1)}_i$    2-1 其中，$n$表示第$l-1$层的神经元个数，$f(z)$表示激活函数

矩阵法求解

假设第$l$层有$p$个神经元，第$l-1$层有$n$个神经元，则代数式$z^{(l)}_i=\sum\limits_{j=1}^n w^{(l-1)}_{ij}a^{(l-1)}_j+b^{(l-1)}_i$中的$w^{(l-1)}_{ij}$、$z^{(l)}_i$和$b^{(l-1)}_i$用矩阵形式分别可表示为：

$W^{(l-1)}=\left[ \begin{array}{cc}w^{(l-1)}_{11}&w_{12}^{(l-1)}&w_{13}^{(l-1)}&...&w_{1n}^{(l-1)}\\w_{21}^{(l-1)}&w_{22}^{(l-1)}&w_{23}^{(l-1)}&...&w_{2n}^{(l-1)}\\.&.&.&...&.\\w_{p1}^{(l-1)}&w_{p2}^{(l-1)}&x_{p3}^{(l-1)}&...&x_{pn}^{(l-1)} \end{array} \right]_{p \times n}$ ,$a^{(l-1)}=\left[ \begin{array}{cc}a^{(l-1)}_1\\a^{(l-1)}_2\\...\\a^{(l-1)}_n \end{array} \right]_{n \times 1}$，$b^{(l-1)}=\left[ \begin{array}{cc}b^{(l-1)}_1\\b^{(l-1)}_2\\...\\b^{(l-1)}_p \end{array} \right]_{p \times 1}$, $z^{(l)}=\left[ \begin{array}{cc}z^{(l)}_1\\z^{(l)}_2\\...\\z^{(l)}_m \end{array} \right]_{p \times 1}$ ，故

$矩阵形式为：z^{(l)}=W^{(l-1)}a^{(l-1)}+b^{(l-1)}$     2-2

$a^{(l)}=f(z^{(l)})=f(W^{(l-1)}a^{(l-1)}+b^{(l-1)})$

定义输出层$L_{nl}$的假设函数为$h_{(W,b)}(x)$，则$h_{(W,b)}(x)=a^{(nl)}=f(W^{(nl-1)}a^{(nl-1)}+b^{(nl-1)})$

参考资料

1. 刘建平Pinard老师的博客https://www.cnblogs.com/pinard/p/6418668.html

2. UFLDL Tutorial

3. 周志华《机器学习》

4. By Michael Nielsen http://neuralnetworksanddeeplearning.com/chap1.html