感知机(Perceptrons)—人工神经元
1957年科学家Frank Rosenblatt 开发了感知机这一人工神经元。感知机是二类分类的线性分类模型,属于判别模型。它由两层神经元组成,输入层接收样本的特征,输出层产生样本的二进制类别。
感知机模型
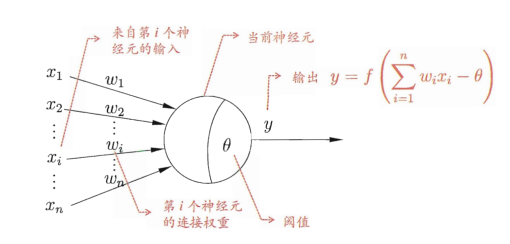
假设我们有m个样本,每个样本有n个特征,对应的输出结果y为-1或1。感知机的工作原理就是输入每个样本的n个特征,并通过带权重的连接将信号传递给下一层神经元,然后将该神经元接收到的总输入值与阈值进行比较,通过“激活函数”(activation function)处理以产生神经元的输出,如果大于阈值,则输出1,否则,输出-1。其基本数学模型表示如下:
$y=\begin{cases} -1,{\,}{\,} if {\,}{\,} \sum \limits_{i=1}^{n}w_ix_i< threshold\\1, {\,}{\,} if {\,}{\,} \sum \limits_{i=1}^{n}w_ix_i>= threshold\end{cases}$ 1-1
使用偏差代替阈值,感知机的简化方式可描述为:
$y=\begin{cases} -1, {\,}{\,} if {\,}{\,} w⋅x +b < 0\\1, {\,}{\,} if {\,}{\,} w⋅x +b >=0\end{cases}$ 1-2 其中,$w$和$x$分别为权重和输入特征的向量,$b$为感知机的偏差(bias),$b=-threshold$,$w⋅x$表示$w$和$x$的内积
令$b=w_0⋅x_0 (x_0=1)$,则感知机模型可进一步简化为$y=sign(w⋅x)$:
$sign(x)=\begin{cases} -1, {\,}{\,} x < 0\\1, {\,}{\,} x >=0\end{cases}$ 1-3
损失函数
感知机的一个假设是训练数据集是线性可分的。如果存在超平面$w⋅x$=0,对于所有类别为1的样本,有$w⋅x>0$,对于所有类别为-1的样本,有$w⋅x<0$,则称训练数据集线性可分,否则,称数据集线性不可分。
假设训练数据集线性可分,感知机学习的目的是求出将训练数据集的正实例点和负实例点完全正确分开的超平面。也就是说要确定模型参数$w$,这就需要定义一个损失函数并将其最小化。感知机所采用的的损失函数是误分类点到超平面的的总距离。
对于误分类样本$i$,满足$-y^{(i)}(w⋅x^{(i)} )>0$,到超平面的距离为$-\frac{1}{||w||}y^{(i)}w⋅x^{(i)}$,这里$||w||$是$w$的L2范数。
假设误分类样本的集合为$M$,则所有误分类点到超平面的总距离为$-\frac{1}{||w||}\sum\limits_{x^{(i)}\in M}y^{(i)}w⋅x^{(i)}$
不考虑$||w||$,就可以得到感知机学习的损失函数:
$J(w)=-\sum\limits_{x^{(i)}\in M}y^{(i)}w⋅x^{(i)}$ 2-1
感知机学习算法
感知机学习问题可转化为损失函数的最优化问题:求参数$w$,使感知机损失函数取极小值
$\min\limits_{w} J(w)=-\sum\limits_{x^{(i)}\in M}y^{(i)}w⋅x^{(i)}$
感知机模型算法的原始形式
对于感知机损失函数的最优化,具体采用随机梯度下降法( stochastic gradient descent),每次随机选取一个误分类点使其梯度下降。
对$w$求偏导,$\frac{\partial J(w)}{\partial w}=-\sum\limits_{x^{(i)}\in M}y^{(i)}x^{(i)}$,随机选取第$i$个误分类样本计算梯度,迭代公式为
$w=w+\alpha y^{(i)}x^{(i)}$ 3-1
式3-1中,$\alpha$ (0< $\alpha$ <=1 )是步长,在统计学上也称为学习率;$y^{(i)}$为样本输出1或者-1,$x^{(i)}$为(n+1)x1的向量。
假设我们有m个样本,每个样本有n个特征,对应的输出结果y为-1或1。算法的具体步骤为:
- 选取$w$初始值,记为$w_0$,设置步长$\alpha$。如$w_0=0$,$\alpha=1$
- 依次选择训练数据集中的样本$(x^{(i)},y^{(i)})$
- 对于满足$-y^{(i)}(w⋅x^{(i)} )>0$的误分类样本,进行$w$更新迭代:$w=w+\alpha y^{(i)}x^{(i)}$
- 再回到步骤b,直至训练集中没有误分类点。
当训练集线性可分时,以上迭代方式是收敛的,也就是说通过有限次的搜索可以找到将训练数据集中正例和负例完全分开的超平面。但也要注意,会存在多个超平面,主要依赖于初始值的选择及迭代过程中误分类点的选择顺序。如果想要得到唯一的超平面,需要对分离超平面添加约束条件。
感知机模型算法的对偶形式
除了以上原始形式,感知机算法也可以采用对偶形式。其基本思想是:将 $w$ 表示为特征输入 $x^{(j)}$和类别输出 $y^{(j)}$的线性组合形式,然后求解其系数而求得 $w$。
对于离超平面较近的误分类点,可能需要进行多次迭代更新才能不被误判。比如说,有误分类样本$(x^{(j)},y^{(j)})$,经过了$m^{(j)}$次修改(迭代),假设$w$初值为0,则
$w=m^{(j)}\alpha y^{(j)}x^{(j)}$
因此,训练集中所有样本最后学习得到的$w$可表示为
$w=\sum\limits_{j=1}^m m^{(j)}\alpha y^{(j)}x^{(j)}$ 其中,$j=1,2,...,m$,m表示样本个数
此时,误分类条件可改为$-y^{(i)}\sum\limits_{j=1}^m m^{(j)}\alpha y^{(j)}x^{(j)}⋅x^{(i)}>0$
假设我们有m个样本,每个样本有n个特征,对应的输出结果y为-1或1。算法的具体步骤为:
- 选取$m$初始值为0,设置步长$\alpha=1$
- 计算所有样本内积形成的Gram矩阵G
- 依次选择训练数据集中的样本$(x^{(i)},y^{(i)})$
- 对于满足$-y^{(i)}\sum\limits_{j=1}^m m^{(j)}\alpha y^{(j)}x^{(j)}⋅x^{(i)} >0$的误分类样本,进行$m^{(i)}\alpha$更新迭代:$m^{(i)}\alpha=(m^{(i-1)}+1)\alpha =m^{(i-1)}\alpha +\alpha$
- 再回到步骤b,直至训练集中没有误分类点。
注:这里需要注意一个概念:Gram矩阵(Gram matrix),样本内积矩阵,$G=[x^{(j)}⋅x^{(i)}]_{m\times m}$,为了节省运行时间,可以预先将训练集中实例间的内积计算出来并以矩阵的形式存储。
参考资料
1. 李航老师的书《统计学方法》
2. 刘建平Pinard老师的博客https://www.cnblogs.com/pinard/p/6042320.html
3. By Michael Nielsen http://neuralnetworksanddeeplearning.com/chap1.html

 浙公网安备 33010602011771号
浙公网安备 33010602011771号