分类模型的性能评估指标总结

机器学习中所用模型的好坏需要通过一些量化的指标来评估。对于分类模型，是通过：1）精度（Accuracy）；2）准确率（Precision）；3）召回率（Recall）；4）F1分数；5）ROC曲线（Receiver operating characteristic curve，受试者工作特征曲线）；6）AUC（Area Under Curve）曲线来实现的。

二分类模型

对于二分类问题，通常将两个类别称为正类和负类。正类中的样本为正例，负类中的样本为负例。假设我们有一组样本对应的y真实标签记为y_test = [1 1 0 1 1 1]，相应的y预测标签记为y_pre = [1 0 0 1 0 1]，预测结果可分为4种情况：

• 正例1被判定为正例1，其数目称为TP(True positive)
• 正例1被判定为负例0，其数目称为FN(False negative)
• 负例0被判定为正例1，其数目称为FP(False positive)
• 负例0被判定为负例0，其数目称为TN(True negative)

将预测结果写成混淆矩阵（confusion matrix）形式：

真实标签	预测标签
	正例（1）	负例（0）
正例（1）	TP	FN
负例（0）	FP	TN

 

样本量$N=TP+FP+FN+TN$

精度$Accuracy=\frac{TP+TN}{TP+FP+FN+TN}$，表示总样本中预测正确的样本数占比。

错误率$Error=1-Accuracy=\frac{FP+FN}{TP+FP+FN+TN}$

查准率$Precision=\frac{TP}{TP+FP}$，也称为准确率，表示预测值为正的样本中预测正确的样本数占比。

召回率$Recall=\frac{TP}{TP+FN}$，也称为查全率，表示真实值为正的样本中预测正确的样本数占比，即正样本的准确率。

注：查准率和查全率是一对矛盾的度量。一般来说，查准率高时，查全率往往偏低；而查全率高时，查全率往往偏低。

Precision-Recall 曲线是根据多个阈值计算得到的多组查准率（纵坐标）和查全率（横坐标）绘制而成，示意图如下：

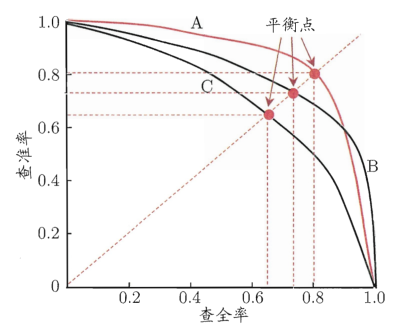
从P-R图上可以直观地看到模型在样本总体上的查准率和查全率。当一个模型的P-R曲线被另一个模型的曲线完全包住，则可认为后者的性能优于前者（上图中A优于C）；如果两个模型的P-R曲线发生了交叉，则难以一般性地判断两者孰优孰劣，只能在具体得查准率或查全率条件下比较（上图中A和B）。当然，如果非要比较上图中A和B模型的相对好坏，可通过计算平衡点（Break-Event Point，即查准率=查全率的点）的值来比较，则可认为模型A优于B。更常用的度量方式则为F1评分。

F1评分$F1$ $score=\frac{2*Precision*Recall}{Precision+Recall}$

ROC曲线是根据多个阈值计算得到的多组FPR(False positvie rate，假正例率) （作为横坐标）和 TPR (True positvie rate，真正例率)（作为纵坐标）绘制而成；其中，

• $TPR=\frac{TP}{TP+FN}$，与召回率的公式一样
• $FPR=\frac{FP}{FP+TN}$，表示真实值为负的样本中预测错误的样本数占比，等于1-特异度（Specificity）

可以看到，ROC曲线同时考虑了分类模型对正例和负例的分类能力，对样本类别是否均衡并不敏感，因此，常被用来评价模型的性能。其值越靠上说明模型越好。与P-R图类似，当一个模型的ROC曲线被另一个模型的曲线完全包住，则可认为后者的性能优于前者；如果两个模型的ROC曲线发生了交叉，则难以一般性地判断两者孰优孰劣。如果非要比较，比较合理的判据是比较ROC曲线下的面积，即AUC。

AUC表示ROC曲线下面的面积，值范围为0~1。其值越高，模型性能越好；AUC=1.0时模型最好，AUC=0.5表示随机分类。