逻辑回归原理总结

在线性回归模型中，拟合函数$h(x)$输出一组连续型标签值。当标签是离散型变量，或者说想做分类任务，可通过引入联系函数（link function）， 得到一个“广义线性模型”实现分类。

二分类模型

对于二分类模型，Sigmoid函数正是这样一个联系函数：

$y=\frac{1}{1+e^{-h(x)}}$ 1-1

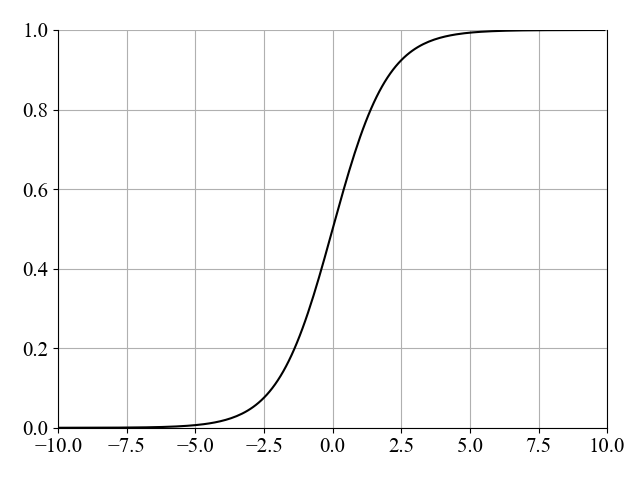
注：Sigmoid函数是指形似S型的函数，自变量趋近于正无穷时，因变量无限趋近于1，自变量趋近于负无穷时，因变量无限趋近于0，但不能取到0和1这两个值。与感知机相比，Sigmoid 神经元经过修改，使其权重和偏差的微小变化仅导致其输出发生微小变化。有时也将Sigmoid函数称为逻辑函数。

 

若将$y$视为样本$x$作为正例的可能性，则$1-y$是其反例可能性，两者的比值称为"几率(odds)"，反映了$x$作为正例的相对可能性，对几率取对数则得到"对数几率"（log odds）

$ln{\frac{y}{1-y}}=ln{\frac{\frac{1}{1+e^{-\theta^Tx}}}{1-\frac{1}{1+e^{-\theta^Tx}}}}=ln{\frac{1}{e^{-\theta^Tx}}}=\theta^Tx$      1-2

从上面式子可以看到，线性回归中用到Sigmoid函数其实就是对数几率函数，对线性回归模型的预测结果取对数几率使其结果无限逼近0和1。因此，对应的模型称为“对数几率回归”（logistic regression）。我们平时提到的逻辑回归，指的就是对数几率回归。其数学目的是求解能够让模型对数据拟合程度最高的参数$\theta$，以此构建预测函数$y$,然后将特征矩阵输入预测函数来计算逻辑回归的结果。

逻辑回归的损失函数

逻辑回归的损失函数是由极大似然估计推导而来的。

具体推导过程：假设有两个标签0和1（二分类问题），若将1-1式中的$y$视为类后验概率估计$p(y=1|x)$,带入1-2式中，可得

$p(y=1|x)=\frac{1}{1+e^{-\theta^Tx}}$   1-3

$p(y=0|x)=\frac{e^{-\theta^Tx}}{1+e^{-\theta^Tx}}$   1-4

1-3和1-4合并可改写为：

$p(y|x)=p(y=1|x)^{y}(1-p(y=1|x))^{1-y}$   1-5

似然函数为：

$L(\theta)=\prod\limits_{j=1}^{m}p(y=1|x^{(j)})^{y^{(j)}}(1-p(y=1|x^{(j)}))^{1-y^{(j)}} $    1-6

对似然函数取对数后再乘以$-\frac{1}{m}$，即得损失函数：

$J(\theta)=-\frac{1}{m}lnL(\theta)=-\frac{1}{m}\sum\limits_{j=1}^m(y^{(j)}lnp(y=1|x^{(j)})+(1-y^{(j)})ln(1-p(y=1|x^{(j)})))$    代数式1-7

多分类模型

对于多分类问题，最经典的拆分策略有三种：OvO (one vs. one，一对一)、OvR (one-vs-rest，一对其余)和MvM (many vs. many, 多对多)。对于N个类别的多分类学习，

• OvO是指将N个类别两两配对，产生$N(N-1)/2$个二分类任务。
• OvR是指在N个类别的多分类学习中，每次将一个类的样本作为正例，其他类的所有样本都作为反例来训练N个分类器。
• MvM是指每次将若干个类作为正类，若干个其他类作为反类。

总结

对于逻辑回归，虽然名字中有“回归”二字，实际上却是一种分类学习方法。

逻辑回归既可以用来处理二分类问题，也可以用来做多分类。在二分类中，使用Sigmoid函数作为联系函数；在多分类中，采用Softmax函数作为联系函数。

对数几率回归的优点：

• 对线性关系的拟合效果非常好
• 计算快，优于SVM和随机森林
• 输出结果不仅预测出类别，还可得到近似概率预测
• 抗噪能力强