最大正方形

题目 

 

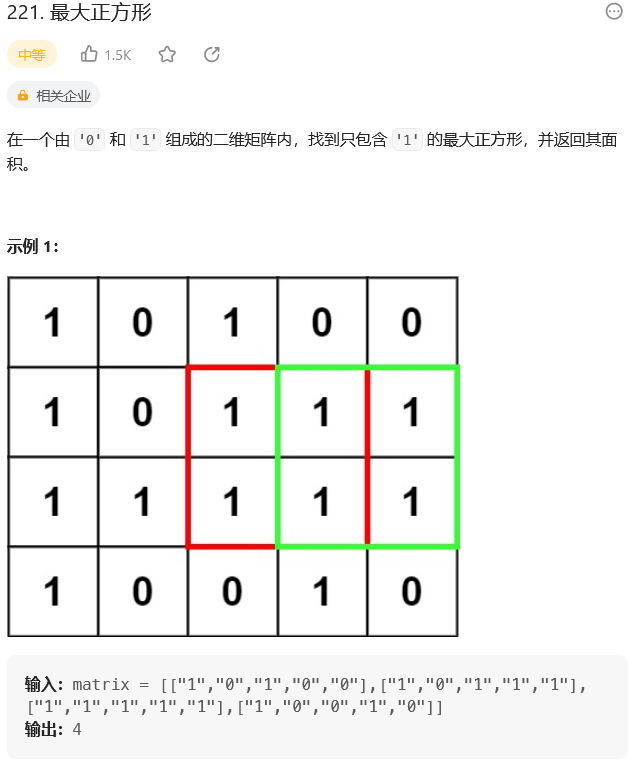
思路分析

1.确定了扫描顺序为从上到下,从左到右,那么需要一个方式来确认以当前点为正方形的右下角

2.采用  dp[i][j] = min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1; 的方式,这个方式的前提是需要当前位置值是 1 ,

如果是0的话,那么你就不满足成为正方形的一部分的概念,所以需要有前置条件  matrix[i][j] != '0'.

那么现在分析公式的可行性:

由于当扫瞄第一行和第一列的时候,其实上面的公式都是不符合的,因为会出现数组溢出的情况,而且,他们要判断成为正方形的话只能判断自身

所以需要进行特殊处理

if (j == 0){
　　dp[i][0] = matrix[i][0] - '0';
}else if (i == 0){
　　dp[0][j] = matrix[0][j] - '0';
}

如果它们是1,那么自身就是一个数值为1的小正方形,不考虑往左和往上扩张的情况

由于公示中涉及到了当前节点位置的左方和上方与左上方的节点,这些都是已经被处理过的,

所以当值为

{'1','0','1','1','1'}
{'1','1','1','1','1'}
{'1','1','1','1','1'}

这时候 动态规划dp数组里面的值为

[[1, 0, 1, 1, 1],

 [1, 1, 1, 2, 2],

 [1, 2, 2, 2, 3]]

 

当值为

{'1','1','1','1','1'},
{'1','1','1','1','1'},
{'1','1','1','1','1'},
{'1','1','1','1','1'}

动态规划dp数组里面的值为

[[1, 1, 1, 1, 1], 
 [1, 2, 2, 2, 2], 
 [1, 2, 3, 3, 3],
 [1, 2, 3, 4, 4]]

 

所以只有当前值的数据是1的时候,且动态规划内的左方,上方和左上方的值中的最小值,才是他可拓展的极限值

代码展示

 

private static int min(int a,int b,int c){
    return Math.min(a,Math.min(b,c));
}

public static int maximalSquare(char[][] matrix) {
    if(matrix == null) return 0;

    int m = matrix.length;
    int n = matrix[0].length;
    //dp[i][j] 以matrix[i][j]为右下角的 全是1的正方形的最大边长 可以以左上角为研究对象 但是麻烦一些
    int[][] dp = new int[m][n];

    int maxLength = 0;
    for(int i = 0;i<m;i++){
        for(int j = 0;j<n;j++){
            //针对第一行和第一列的情况进行特殊处理
            if (j == 0){
                dp[i][0]  = matrix[i][0] - '0';
            }else if (i == 0){
                dp[0][j] = matrix[0][j] - '0';
            }else {
                //没必要用递归计算
                if(matrix[i][j]=='0'){
                    continue;
                }
                dp[i][j] = min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1;

            }
            // 因为每次计算后的数值就是这个节点所能形成最大的正方形的边距,
            // 所以直接保存免得计算完后还需要二次遍历查找
            maxLength = Math.max(maxLength,dp[i][j]);
        }
    }
    System.out.println(Arrays.deepToString(dp));
    return maxLength*maxLength;
}