354. 俄罗斯套娃信封问题

题目：

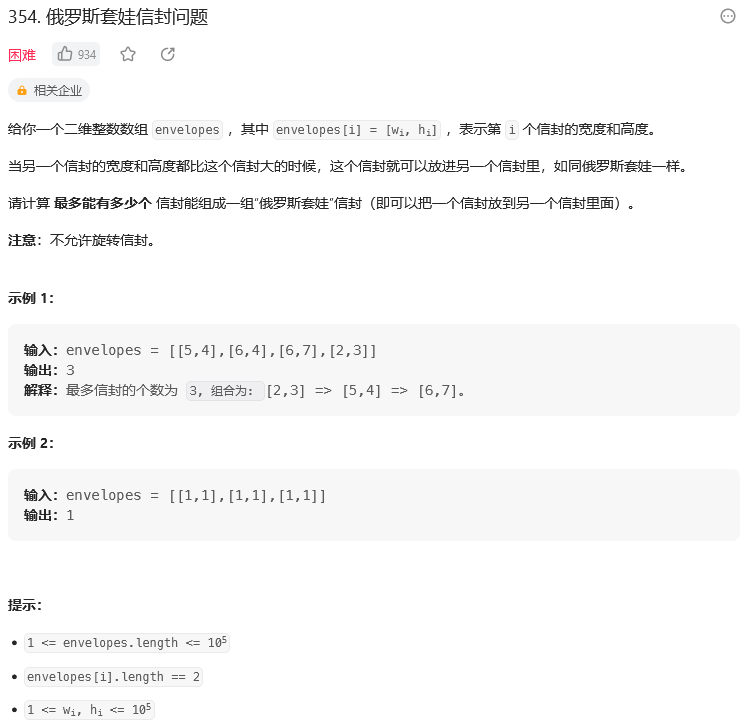
思路：

【1】这道题其实和 最长严格递增子序列 逻辑是一样的，所以其实可以参考  300. 最长递增子序列 这道题。

因为本质上 ：
如数据 [[2, 100], [3, 200], [4, 300], [5, 250], [5, 400], [5, 500], [6, 360], [6, 370], [7, 380]]
你会发现你需要判断是否要选 [4, 300] 这个元素，如果你选了是否会截断后面的填充
后面填充的会不会更大，所以一般会采用辅助空间的方式来记录，能够连起来的数据。

 

代码展示：

//时间49 ms 击败 32.90%
//内存92.8 MB 击败 89.29%
class Solution {
    public int maxEnvelopes(int[][] envelopes) {
        if (envelopes.length == 0) {
            return 0;
        }
        
        int n = envelopes.length;
        Arrays.sort(envelopes, new Comparator<int[]>() {
            public int compare(int[] e1, int[] e2) {
                if (e1[0] != e2[0]) {
                    return e1[0] - e2[0];
                } else {
                    return e2[1] - e1[1];
                }
            }
        });

        List<Integer> f = new ArrayList<Integer>();
        f.add(envelopes[0][1]);
        for (int i = 1; i < n; ++i) {
            int num = envelopes[i][1];
            if (num > f.get(f.size() - 1)) {
                f.add(num);
            } else {
                int index = binarySearch(f, num);
                f.set(index, num);
            }
        }
        return f.size();
    }

    public int binarySearch(List<Integer> f, int target) {
        int low = 0, high = f.size() - 1;
        while (low < high) {
            int mid = (high - low) / 2 + low;
            if (f.get(mid) < target) {
                low = mid + 1;
            } else {
                high = mid;
            }
        }
        return low;
    }
}

//时间33 ms 击败 99.57%
//内存93.6 MB 击败 69.34%
class Solution {
    public int maxEnvelopes(int[][] envelopes) {
        int max = Integer.MIN_VALUE;
        int min = Integer.MAX_VALUE;
        for (int[] envelop : envelopes) {
            int val = envelop[0];
            max = Math.max(max, val);
            min = Math.min(min, val);
        }
        
        int len = max - min + 1;
        PriorityQueue<Integer>[] queues = new PriorityQueue[len];
        for (int[] envelop : envelopes) {
            int val = envelop[0] - min;
            if (queues[val] == null) {
                queues[val] = new PriorityQueue<Integer>((a, b) -> b - a);
            }
            queues[val].offer(envelop[1]);
        }

        int[] stack = new int[len];
        int size = 0;
        int maxH = 0;
        for (PriorityQueue<Integer> queue : queues) {
            if (queue == null) {
                continue;
            }
            int val = 0;
            while (!queue.isEmpty() && queue.peek() > maxH) {
                val = queue.peek();
                queue.poll();
            }
            while (!queue.isEmpty() && queue.peek() == maxH) {
                queue.poll();
            }
            if (val != 0) {
                stack[size++] = val;
                maxH = val;
            }
            int index = size;
            while (!queue.isEmpty()) {
                val = queue.poll();
                if (index == 0) {
                    stack[index] = val;
                    continue;
                }
                index=binarySearch(stack, 0, index, val);
                stack[index] = val;
                if (index == size - 1) {
                    maxH = val;
                }
            }
        }
        return size;
    }

    int binarySearch(int[] nums, int start, int end, int target) {
        while (start < end) {
            int mid = (start + end) >> 1;
            int midValue = nums[mid];
            if (target == midValue) {
                start = mid;
                break;
            } else if (target < midValue) {
                end = mid;
            } else {
                start = mid + 1;
            }
        }
        return start;
    }
}