240. 搜索二维矩阵 II

题目：

思路：

【1】二分的方式进行查找

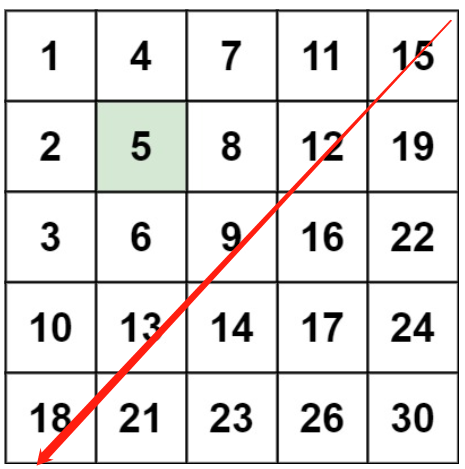
【2】Z 字形查找（这个是能说是符合该题的逻辑要求，因为如果小于15，那么必然不可能大于15下面的，所以会退到11，如果比11大则说明第一行 的都不符合，就会落到下一行，相当于每一次操作都会排除一行或者一列）

 

 

代码展示：

【1】二分的方式进行查找

//时间6 ms 击败 42.45%
//内存48.7 MB 击败 17.43%
//时间复杂度：O(mlog⁡n)。对一行使用二分查找的时间复杂度为 O(log⁡n)，最多需要进行 m 次二分查找。
//空间复杂度：O(1)。
class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int n = matrix[0].length;
        for (int[] data : matrix){
            //下面这两个可以看做是剪枝判断加快程序进程
            if (data[n-1] < target) continue;
            if (data[0] > target ) break;
            if (target == binarySearchTarget(data,target)) return true;
        }
        return false;
    }

    /**
     * 利用二分的方式查找，目标值是否在一维数组中
     * @param data
     * @param target
     * @return
     */
    public int binarySearchTarget(int[] data ,int target){
        int left = 0 , right = data.length - 1;
        while (left <= right){
            int min = (right - left) / 2 + left;
            if (data[min] > target){
                right = min - 1;
            }else if (data[min] < target){
                left = min + 1;
            }else {
                return target;
            }
        }
        return data[left];
    }
}

【2】Z 字形查找

//时间5 ms 击败 98.92%
//内存48.7 MB 击败 16.62%
//时间复杂度：O(m+n)。
//在搜索的过程中，如果我们没有找到 target，那么我们要么将 y 减少 1，要么将 x 增加 1。
//由于 (x,y)的初始值分别为 (0,n−1)，因此 y 最多能被减少 n 次，x 最多能被增加 m 次，总搜索次数为 m+n。
//在这之后，x 和 y 就会超出矩阵的边界。
//空间复杂度：O(1)。
class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length, n = matrix[0].length;
        int x = 0, y = n - 1;
        while (x < m && y >= 0) {
            if (matrix[x][y] == target) {
                return true;
            }
            if (matrix[x][y] > target) {
                --y;
            } else {
                ++x;
            }
        }
        return false;
    }

}