41. 缺失的第一个正数

题目：

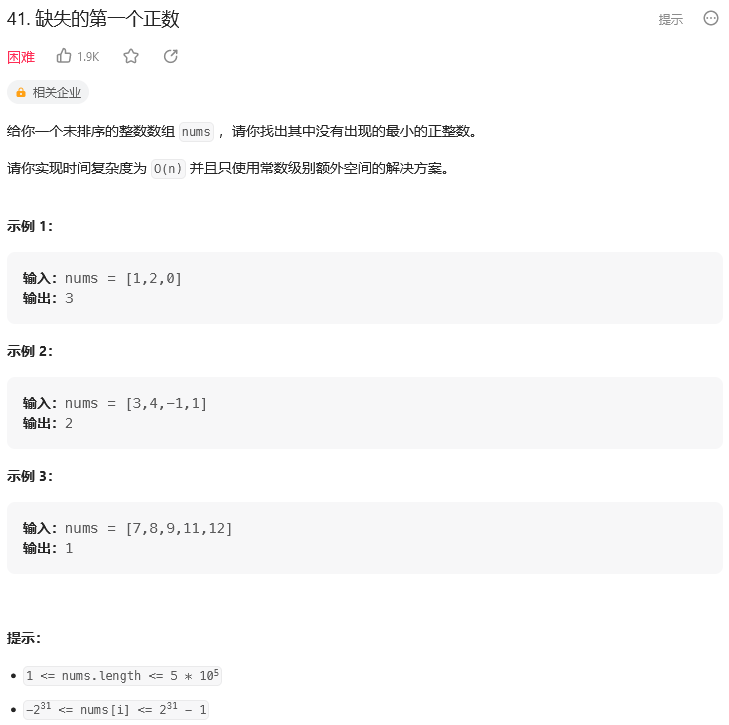
思路：

【1】利用数组下标映射的方式来做

【2】更简单的置换方式

代码展示：

【1】利用数组下标映射的方式来做

//时间1 ms 击败 97.45%
//内存57.8 MB 击败 34.15%
//时间复杂度：O(N)，其中 N 是数组的长度。
//空间复杂度：O(1)。
class Solution {
    /**
     * 因为题目其实是要选找【1-n】的缺失
     * 而对应的数组的下标刚好有【0-n-1】所以可以进行转化
     * 如果存在K ，1<=k<=n,那么就将（k-1）位置的值变为负数
     * 所以理论上应该先将数组中的负数清除，怎么清楚呢，将负数的值变为比N更大的某个数（因为反正都用不到，也找不到下标的）
     * @param nums
     * @return
     */
    public int firstMissingPositive(int[] nums) {
        int n = nums.length;
        // 先将负数清除，保证后面使用到负数标明数值重复的时候不会冲突
        for (int i = 0; i < n; ++i) {
            if (nums[i] <= 0) {
                nums[i] = n + 1;
            }
        }
        // 如果存在某数值k（1<= k <= n）则将k-1的位置上的数值记为负数
        for (int i = 0; i < n; ++i) {
            int num = Math.abs(nums[i]);
            //防止数组越界且如果K存在多次只进行一次修改
            if (num <= n && nums[num - 1] > 0) {
                nums[num - 1] = -nums[num - 1];
            }
        }
        //找出缺乏的下标，那么也就知道对应的数值了
        for (int i = 0; i < n; ++i) {
            if (nums[i] > 0) {
                return i + 1;
            }
        }
        return n + 1;
    }
}

【2】更简单的置换方式

//时间1 ms 击败 97.45%
//内存57.8 MB 击败 35.1%
//更简单的置换方式
//同样是利用【1 ~ n】 与【0 ~ n-1】的映射关系
//每个值放在他对应的下标下面（这里要防止数组越界，同时防止死循环）
//那么其他的不能放在对应位置上的就是缺失的了
class Solution {
    public int firstMissingPositive(int[] nums) {
        int n = nums.length;
        for (int i = 0; i < n; ++i) {
            while (nums[i] > 0 && nums[i] <= n && nums[nums[i] - 1] != nums[i]) {
                int temp = nums[nums[i] - 1];
                nums[nums[i] - 1] = nums[i];
                nums[i] = temp;
            }
        }
        for (int i = 0; i < n; ++i) {
            if (nums[i] != i + 1) {
                return i + 1;
            }
        }
        return n + 1;
    }
}