287. 寻找重复数

题目：

思路：

【1】前置尝试

【2】利用快慢指针检测环的方式（关键是要理解如何将输入的数组看作为链表）

将数组下标 n 和数 nums[n] 建立一个映射关系 f(n)：
1)数组中没有重复的数以数组 [1,3,4,2]为例:
其映射关系 n->f(n)为： 0->1 , 1->3 , 2->4 , 3->2
即先将k->v展示出来，而V又做为下一次的K拿到下一个v，来形成链表。
故组合为 0->1->3->2->4->null

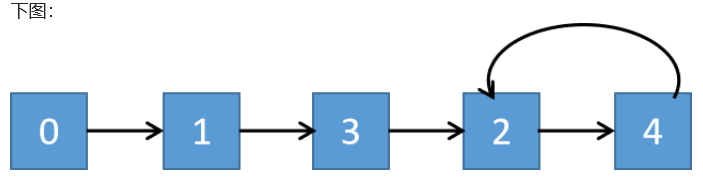
2)数组中有重复的数，以数组 [1,3,4,2,2] 为例:
其映射关系 n->f(n) 为： 0->1 , 1->3 , 2->4 , 3->2 , 4->2
故组合为 0->1->3->2->4->2->4->2->……  , 2->4 是一个循环
所以重复的话就会有环。

整个就会变为检测链表是否有环，而有环的汇聚点在哪！！
参考： 剑指 Offer II 022. 链表中环的入口节点（142. 环形链表 II && 141. 环形链表）

【3】二分查找

代码展示：

【1】前置尝试

//时间2 ms 击败 97.99%
//内存55.9 MB 击败 36.80%
//如果对空间复杂度没有要求的话
//但这种明显不行，因为开辟了N个辅助空间
class Solution {
    public int findDuplicate(int[] nums) {
        int[] falg = new int[nums.length];
        for (int tem : nums){
            if (falg[tem] == 0){
                falg[tem]++;
            }else {
                return tem;
            }
        }
        return -1;
    }
}

//其次由于要求复杂度为O(1)
//所以如果采用最笨的方法，就是双循环
//虽然时间复杂度为O(N^2),但是空间复杂度符合呀
//然后试了下，发现超时了
class Solution {
    public int findDuplicate(int[] nums) {
        for (int i = 0; i < nums.length-1; i++){
            for (int j = i+1; j < nums.length; j++){
                if (nums[i] == nums[j]) return nums[i];
            }
        }
        return -1;
    }
}

【2】利用快慢指针检测环的方式（关键是要理解如何将输入的数组看作为链表）

//时间4 ms 击败 92.92%
//内存55.3 MB 击败 46.52%
//时间复杂度：O(n)。「Floyd 判圈算法」时间复杂度为线性的时间复杂度。
//空间复杂度：O(1)。我们只需要常数空间存放若干变量。
//这种是限定了必定有环的情况
class Solution {
    public int findDuplicate(int[] nums) {
        int slow = 0;
        int fast = 0;

        do{
            slow = nums[slow];
            fast = nums[nums[fast]];
        }while (slow != fast);

        fast = 0;
        while (slow != fast) {
            slow = nums[slow];
            fast = nums[fast];
        }
        return fast;
    }
}

//时间4 ms 击败 92.92%
//内存55.3 MB 击败 46.52%
//这种是增加处理如果不存在环的情况
class Solution {
    public int findDuplicate(int[] nums) {
        int n = nums.length;
        int slow = 0;
        int fast = 0;
        //获取首节点
        slow = nums[slow];
        //获取首节点的下一个节点
        fast = nums[nums[fast]];
        //两个节点不相同
        while(slow != fast){
            // 慢节点走一步
            slow = nums[slow];
            // 快节点走两步
            if (fast < n && nums[fast] < n){
                fast = nums[nums[fast]];
            }else {
                // 遍历到了最后的节点即null的情况，说明没有环
                return -1;
            }
        }
        // 如果存在环
        int pre1 = 0;
        int pre2 = slow;
        // 各自走一步，知道相遇即环的入口位置
        while(pre1 != pre2){
            pre1 = nums[pre1];
            pre2 = nums[pre2];
        }
        return pre1;
    }
}

【3】二分查找

//时间25 ms 击败 33.47%
//内存55.2 MB 击败 53.28%
//时间复杂度：O(nlog⁡n)，其中 n 为 nums 数组的长度。
//二分查找最多需要二分 O(log⁡n) 次，每次判断的时候需要O(n) 遍历 nums 数组求解小于等于 mid 的数的个数，因此总时间复杂度为 O(nlog⁡n)。
//空间复杂度：O(1)。我们只需要常数空间存放若干变量。
class Solution {
    public int findDuplicate(int[] nums) {
        int len = nums.length; // n + 1 = len, n = len - 1

        // 在 [1..n] 查找 nums 中重复的元素
        int left = 1;
        int right = len - 1;
        while (left < right) {
            int mid = (left + right) / 2;

            // nums 中小于等于 mid 的元素的个数
            int count = 0;
            for (int num : nums) {
                if (num <= mid) {
                    count++;
                }
            }

            if (count > mid) {
                // 下一轮搜索的区间 [left..mid]
                right = mid;
            } else {
                // 下一轮搜索的区间 [mid + 1..right]
                left = mid + 1;
            }
        }
        return left;
    }
}