74. 搜索二维矩阵

题目：

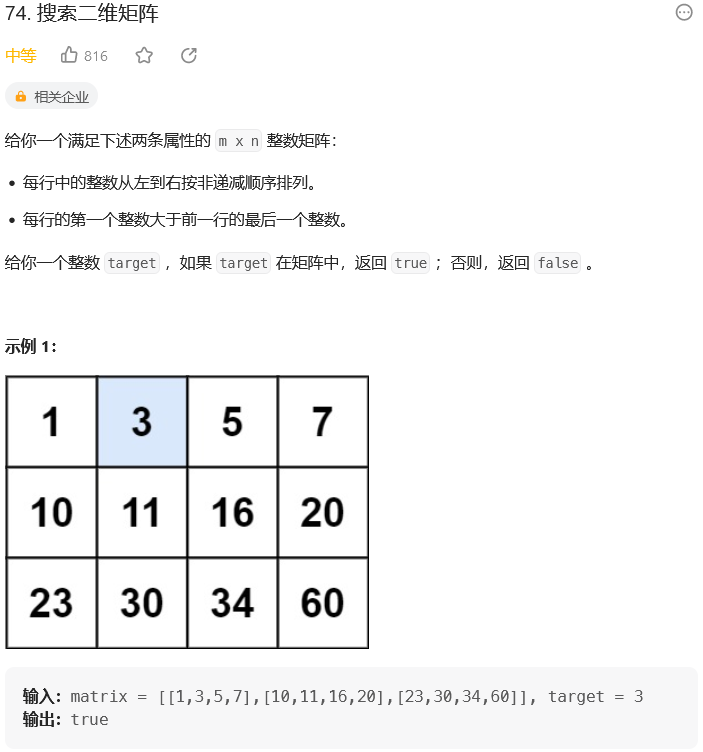
思路：

【1】利用二分进行优化

代码展示：

//时间0 ms 击败 100%
//内存40.2 MB 击败 35.97%
class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int row = matrix.length, col = matrix[0].length;
        while (row-- > 0){
            if (matrix[row][0] > target) continue;
            else {
                for (int i = 0; i < col; i++){
                    if (matrix[row][i] == target) return true;
                }
            }
        }
        return false;
    }
}


//一次二分优化
//时间0 ms 击败 100%
//内存39.5 MB 击败 99.45%
//时间复杂度：O(log⁡mn)，其中 m 和 n 分别是矩阵的行数和列数。
//空间复杂度：O(1)。
class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int row = matrix.length;
        while (row-- > 0){
            if (matrix[row][0] > target) continue;
            else {
                // 这里可以用二分查找进行优化
                int left = 0, right = matrix[0].length-1;
                while (left < right){
                    int min = left + (right-left)/2;
                    if (matrix[row][min] > target){
                        right = min - 1;
                    }else if (matrix[row][min] == target){
                        return true;
                    }else {
                        left = min + 1;
                    }
                }
                if ( matrix[row][left] == target) return true;
            }
        }
        return false;
    }
}


//用两次二分进行优化
//时间0 ms 击败 100%
//内存40.1 MB 击败 48.89%
//时间复杂度：O(log⁡m+log⁡n)=O(log⁡mn)，其中 m 和 n 分别是矩阵的行数和列数。
//空间复杂度：O(1)。
class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int rowIndex = binarySearchFirstColumn(matrix, target);
        if (rowIndex < 0) {
            return false;
        }
        return binarySearchRow(matrix[rowIndex], target);
    }

    public int binarySearchFirstColumn(int[][] matrix, int target) {
        int low = -1, high = matrix.length - 1;
        while (low < high) {
            int mid = (high - low + 1) / 2 + low;
            if (matrix[mid][0] <= target) {
                low = mid;
            } else {
                high = mid - 1;
            }
        }
        return low;
    }

    public boolean binarySearchRow(int[] row, int target) {
        int low = 0, high = row.length - 1;
        while (low <= high) {
            int mid = (high - low) / 2 + low;
            if (row[mid] == target) {
                return true;
            } else if (row[mid] > target) {
                high = mid - 1;
            } else {
                low = mid + 1;
            }
        }
        return false;
    }
}