4. 寻找两个正序数组的中位数

题目：

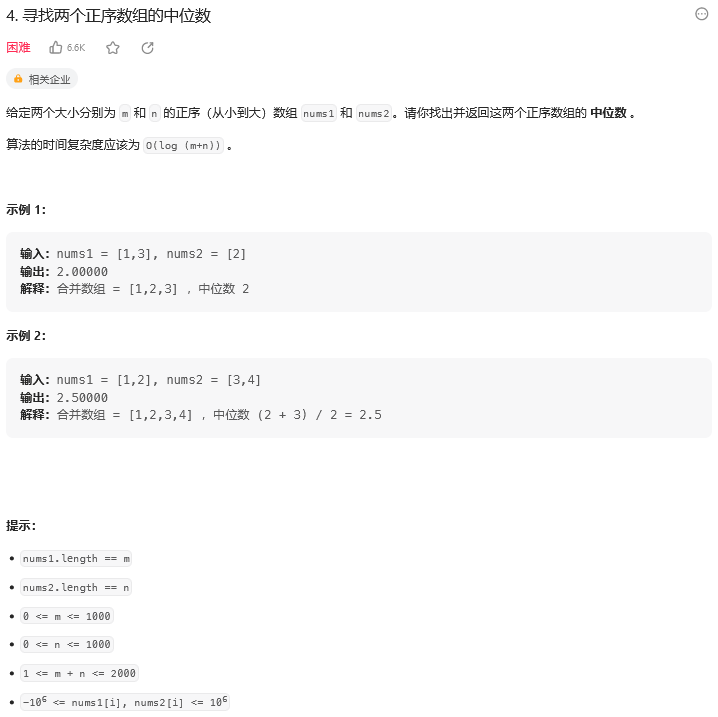
思路：

【1】合并数组排序，然后计算

【2】二分查找

【3】划分数组

代码展示：

【1】合并数组排序，然后计算

//时间3 ms 击败 20.74%
//内存43.3 MB 击败 51.79%
class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int n1 = nums1.length, n2 = nums2.length, n = n1 + n2;
        int[] result = new int[n];
        System.arraycopy(nums1, 0, result, 0, n1);
        System.arraycopy(nums2, 0, result, n1, n2);
        Arrays.sort(result);
        if (n%2 == 1){
            return result[(n-1)/2] * 1.0;
        }else {
            int index = (n-1)/2;
            return (result[index] +  result[index+1] ) / 2.0;
        }
    }
}

【2】二分查找

//时间1 ms 击败 100%
//内存43.6 MB 击败 25.12%
//时间复杂度：O(log⁡(m+n))，其中 m 和 n 分别是数组 nums1 和 nums2 的长度。
//初始时有 k=(m+n)/2 或 k=(m+n)/2+1，每一轮循环可以将查找范围减少一半，因此时间复杂度是 O(log⁡(m+n))。
//空间复杂度：O(1)。
class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int length1 = nums1.length, length2 = nums2.length;
        int totalLength = length1 + length2;
        double median = 0;
        if (totalLength % 2 == 1) {
            int midIndex = totalLength / 2;
            median = getKthElement(nums1, nums2, midIndex + 1);
        } else {
            int midIndex1 = totalLength / 2 - 1, midIndex2 = totalLength / 2;
            median = (getKthElement(nums1, nums2, midIndex1 + 1) + getKthElement(nums1, nums2, midIndex2 + 1)) / 2.0;
        }
        return median;
    }

    /* 主要思路：要找到第 k (k>1) 小的元素，那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 进行比较
     * 这里的 "/" 表示整除
     * nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个
     * nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共计 k/2-1 个
     * 取 pivot = min(pivot1, pivot2)，两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个
     * 这样 pivot 本身最大也只能是第 k-1 小的元素
     * 如果 pivot = pivot1，那么 nums1[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除"，剩下的作为新的 nums1 数组
     * 如果 pivot = pivot2，那么 nums2[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除"，剩下的作为新的 nums2 数组
     * 由于我们 "删除" 了一些元素（这些元素都比第 k 小的元素要小），因此需要修改 k 的值，减去删除的数的个数
     */
    public int getKthElement(int[] nums1, int[] nums2, int k) {
        int length1 = nums1.length, length2 = nums2.length;
        int index1 = 0, index2 = 0;
        int kthElement = 0;

        while (true) {
            // 边界情况
            if (index1 == length1) {
                return nums2[index2 + k - 1];
            }
            if (index2 == length2) {
                return nums1[index1 + k - 1];
            }
            if (k == 1) {
                return Math.min(nums1[index1], nums2[index2]);
            }

            // 正常情况
            int half = k / 2;
            int newIndex1 = Math.min(index1 + half, length1) - 1;
            int newIndex2 = Math.min(index2 + half, length2) - 1;
            int pivot1 = nums1[newIndex1], pivot2 = nums2[newIndex2];
            if (pivot1 <= pivot2) {
                k -= (newIndex1 - index1 + 1);
                index1 = newIndex1 + 1;
            } else {
                k -= (newIndex2 - index2 + 1);
                index2 = newIndex2 + 1;
            }
        }
    }
}

【3】划分数组

//时间1 ms 击败 100%
//内存43.4 MB 击败 47.94%
//时间复杂度：O(log⁡min⁡(m,n)))，其中 m 和 n 分别是数组 nums1 和 nums2 的长度。
//查找的区间是 [0,m]，而该区间的长度在每次循环之后都会减少为原来的一半。
//所以，只需要执行 log⁡m 次循环。由于每次循环中的操作次数是常数，所以时间复杂度为 O(log⁡m)。
//由于我们可能需要交换 nums1 和 nums2 使得 m≤n，因此时间复杂度是 O(log⁡min⁡(m,n)))。
//空间复杂度：O(1)。
class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        if (nums1.length > nums2.length) {
            return findMedianSortedArrays(nums2, nums1);
        }

        int m = nums1.length;
        int n = nums2.length;
        int left = 0, right = m;
        // median1：前一部分的最大值
        // median2：后一部分的最小值
        int median1 = 0, median2 = 0;

        while (left <= right) {
            // 前一部分包含 nums1[0 .. i-1] 和 nums2[0 .. j-1]
            // 后一部分包含 nums1[i .. m-1] 和 nums2[j .. n-1]
            int i = (left + right) / 2;
            int j = (m + n + 1) / 2 - i;

            // nums_im1, nums_i, nums_jm1, nums_j 分别表示 nums1[i-1], nums1[i], nums2[j-1], nums2[j]
            int nums_im1 = (i == 0 ? Integer.MIN_VALUE : nums1[i - 1]);
            int nums_i = (i == m ? Integer.MAX_VALUE : nums1[i]);
            int nums_jm1 = (j == 0 ? Integer.MIN_VALUE : nums2[j - 1]);
            int nums_j = (j == n ? Integer.MAX_VALUE : nums2[j]);

            if (nums_im1 <= nums_j) {
                median1 = Math.max(nums_im1, nums_jm1);
                median2 = Math.min(nums_i, nums_j);
                left = i + 1;
            } else {
                right = i - 1;
            }
        }

        return (m + n) % 2 == 0 ? (median1 + median2) / 2.0 : median1;
    }
}