502. IPO（意思为首次公开募股）

题目：

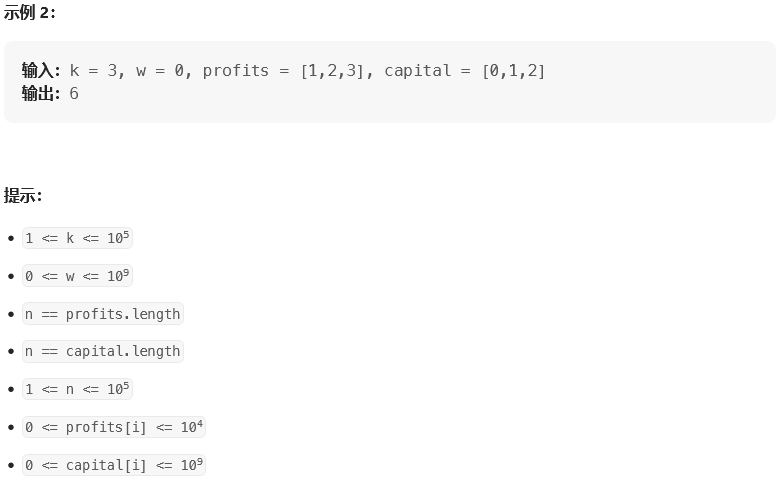
思路：

【1】利用堆的思想（优先队列）来完成贪心的操作，从而满足拿到最大资本

代码展示：

//时间97 ms 击败 29.1%
//内存63.6 MB 击败 21.61%
//时间复杂度：O((n+k)log⁡ n)，其中 n 是数组 profits 和 capital 的长度，k 表示最多的选择数目。
//我们需要 O(nlog⁡n) 的时间复杂度来来创建和排序项目，往堆中添加元素的时间不超过 O(nlog⁡n)，
//每次从堆中取出最大值并更新资本的时间为 O(klog⁡n)，因此总的时间复杂度为 O(nlog⁡n+nlog⁡n+klog⁡n)=O((n+k)log⁡n)。
//空间复杂度：O(n)，其中 n 是数组 profits 和 capital 的长度。
//空间复杂度主要取决于创建用于排序的数组和大根堆。
class Solution {
    public int findMaximizedCapital(int k, int w, int[] profits, int[] capital) {
        int n = profits.length;
        int curr = 0;
        int[][] arr = new int[n][2];

        for (int i = 0; i < n; ++i) {
            arr[i][0] = capital[i];
            arr[i][1] = profits[i];
        }
        Arrays.sort(arr, (a, b) -> a[0] - b[0]);

        PriorityQueue<Integer> pq = new PriorityQueue<>((x, y) -> y - x);
        for (int i = 0; i < k; i++) {
            while (curr < n && arr[curr][0] <= w) {
                pq.add(arr[curr][1]);
                curr++;
            }
            if (!pq.isEmpty()) {
                w += pq.poll();
            } else {
                break;
            }
        }

        return w;
    }
}


//本质上用堆就是为了符合贪心的理念，所以上面的情况用两个堆会更好处理一些
//时间18 ms 击败 99.38%
//内存62.3 MB 击败 26.86%
class Solution {
    /**
     * 最大化最终资本(利用两个堆的方式)
     * @param k  可选项目个数
     * @param w  初始资本
     * @param profits 项目利润集合
     * @param capital 项目成本集合
     * @return 最大化最终资本
     */
    public int findMaximizedCapital(int k, int w, int[] profits, int[] capital) {
        int n = profits.length;
        // 可选堆（所需成本是小于或等于当前持有成本的），可选堆要求利润最大的排前面
        PriorityQueue<Integer> select = new PriorityQueue<>((a, b) -> profits[b] - profits[a]);
        // 不可选堆（所需成本是大于当前持有成本的），可选要求成本小的排前面
        PriorityQueue<Integer> unselect = new PriorityQueue<>((a, b) -> capital[a] - capital[b]);
        for (int i = 0; i < n; i++) {
            //所需成本是小于或等于当前持有成本的加入到可选堆
            if (capital[i] <= w) select.add(i);
            //否则加入到不可选堆
            else unselect.add(i);
        }
        //防止n<k的情况会导致死循环或数据不存在问题
        k = Math.min(k, n);
        while (k > 0 && !select.isEmpty()) {
            int i = select.poll();
            w += profits[i];
            k--;
            // 如果持有成本变更，则要把不可选集合里面的新可选部分塞入到可选集合
            while (!unselect.isEmpty() && w >= capital[unselect.peek()]) {
                select.add(unselect.poll());
            }
        }
        return w;
    }
}