918. 环形子数组的最大和

题目：

思路：

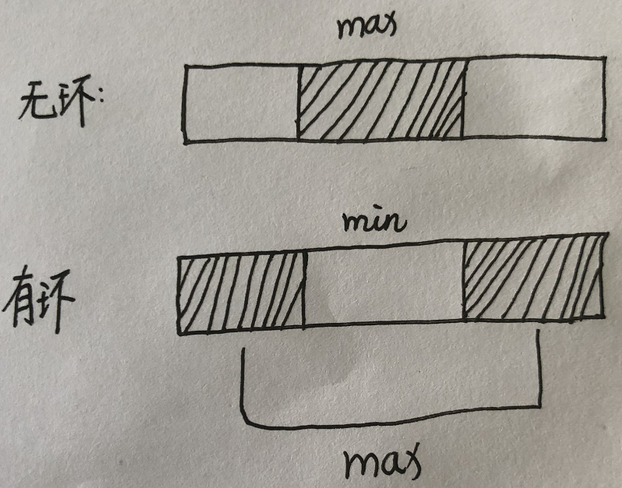
【1】情况分为一下两种：

无环状态下，即为53. 最大子序和
有环状态下，要使得两端之和最大，必须让中间的子数组最小，即最后有环情况下的最大子数组和为：sum(nums)-min_

 

 

 

代码展示：

//时间6 ms 击败 50.69%
//内存45.2 MB 击败 80.17%
class Solution {
    public int maxSubarraySumCircular(int[] nums) {
        int total = 0, maxSum = nums[0], curMax = 0, minSum = nums[0], curMin = 0;
        for (int a : nums) {
            // 这一部分便是正常的不能形成环的情况下的最大连续和
            curMax = Math.max(curMax + a, a);
            maxSum = Math.max(maxSum, curMax);
            // 如果存在环的话那么应该将最小和也求出来，总数减去最小和便是环从最小和这部分切割开后连起来的情况
            curMin = Math.min(curMin + a, a);
            minSum = Math.min(minSum, curMin);
            total += a;
        }

        return maxSum > 0 ? Math.max(maxSum, total - minSum) : maxSum;
    }
}