114. 二叉树展开为链表

题目：

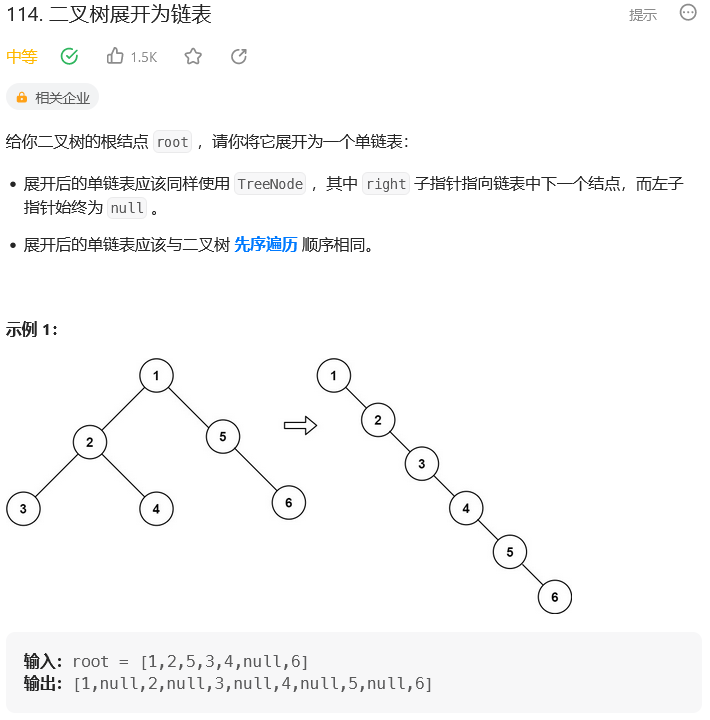
思路：

【1】借助辅助空间的方式

【2】不借助辅助空间纯粹遍历的方式

代码展示：

【1】借助辅助空间的方式

//时间0 ms 击败 100%
//内存40.1 MB 击败 50.85%
//时间复杂度：O(n)。
//空间复杂度：O(n)。
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public void flatten(TreeNode root) {
        if (root == null) return;
        ArrayList<TreeNode> list = new ArrayList<>();
        inorderTraversal(root,list);
        TreeNode temp = null;
        // 由于中序遍历后集合里面的顺序已经是正确的，所以倒序拿出，利用头插法形成链表
        for (int i = list.size()-1; i >= 0; i--){
            TreeNode curr = list.get(i);
            curr.left = null;
            curr.right = temp;
            temp = curr;
        }
    }
    
    // 中序遍历，并将结果集放入集合list中
    public void inorderTraversal(TreeNode root,ArrayList<TreeNode> list){
        if (root == null) return;
        list.add(root);
        inorderTraversal(root.left,list);
        inorderTraversal(root.right,list);
    }
}

【2】不借助辅助空间纯粹遍历的方式

//时间0 ms 击败 100%
//内存39.7 MB 击败 96.81%
class Solution {
    public void flatten(TreeNode root) {
        if (root == null) return;
        deploymentTree(root);
    }

    /**
     * 该展开方法是将树展开成链表
     * 由于是依据中序遍历的，所以根结点是首节点
     * （又是作为入参，默认上层方法中是已获取的）
     * 返回的是：展开后的链表的末尾节点
     * 
     * 将该树分为三部分，根结点，左子树，右子树
     * 那么必然会有 根结点 -> 左子树 -> 右子树
     * 所以形成的链表存在 
     * 1. 左子树 和 右子树 都为空 ， 链表只有 根结点
     * 2. 左子树 为空 ， 链表只有 根结点 -> 右子树
     * 3. 右子树 为空 ， 链表只有 根结点 -> 左子树
     * 4. 左子树 和 右子树 都不为空 ， 链表只有 根结点 -> 左子树 -> 右子树
     * @param root 传入的是子树的根结点
     * @return
     */
    private TreeNode deploymentTree(TreeNode root){
        // 对应情况1. 左子树 和 右子树 都为空 ， 链表只有 根结点（那么链表尾结点是根结点）
        if (root.left == null && root.right == null) return root;
        
        // 下面为 左子树 和 右子树 总有一个不为空的情况
        TreeNode left = root.left , right = root.right;
        TreeNode leftEnd = null , rightEnd = null;
        root.left = null;
        root.right = null;
        if (left != null){
            // 如果 左子树 不为空（情况3,4的前面部分都满足）
            // 3. 右子树 为空 ， 链表只有 根结点 -> 左子树
            // 4. 左子树 和 右子树 都不为空 ， 链表只有 根结点 -> 左子树 -> 右子树
            root.right = left;
            leftEnd = deploymentTree(left);
            
            leftEnd.right = right;
            if (right != null){
                //4. 左子树 和 右子树 都不为空 ， 链表只有 根结点 -> 左子树 -> 右子树
                rightEnd = deploymentTree(right);
            }else {
                // 3. 右子树 为空 ， 链表只有 根结点 -> 左子树
                rightEnd = leftEnd;
            }
        }else {
            // 如果 左子树 为空 ，有已经判断了情况1
            // 那么此时必然是情况2. 左子树 为空 ， 链表只有 根结点 -> 右子树
            // （那么链表尾结点是右子树的末尾节点）
            root.right = right;
            rightEnd = deploymentTree(right);
        }
        return rightEnd;
    }
}