221. 最大正方形

题目：

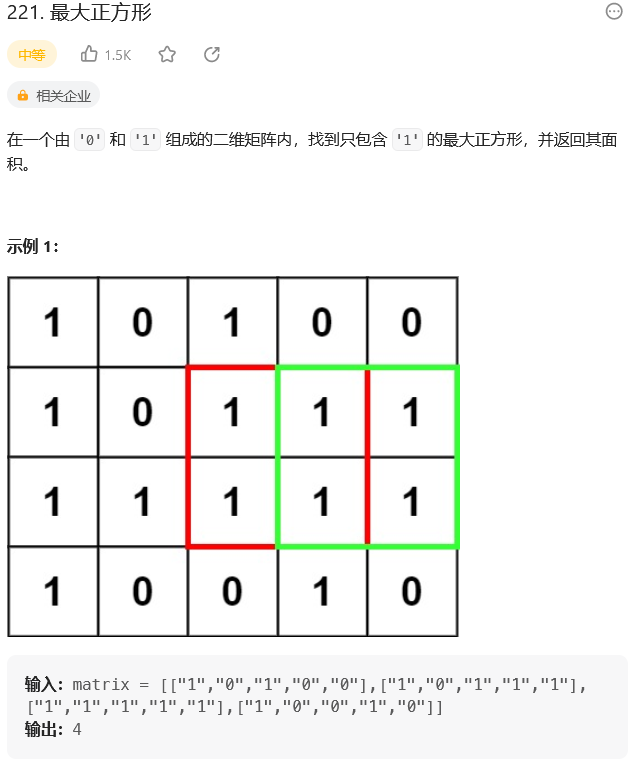
思路：

【0】本来一开始打算参考  剑指 Offer II 040. 矩阵中最大的矩形（85. 最大矩形）这篇，原因是十分相似，后来发现倒不如原生的操作会比较快。

【1】动态规划的思想，借助辅助空间将一些计算过的数值记录，减少遍历的次数

代码展示：

//时间43 ms 击败 10.95%
//内存50.8 MB 击败 94.83%
class Solution {
    public int maximalSquare(char[][] matrix) {
        int row = matrix.length;
        int col = matrix[0].length;
        int[] height = new int[col];
        int max = 0;
        for (int i = 0; i < row; i++){
            updateHeights(height, matrix[i]);
            max = Math.max(max, largestSquareArea(height,matrix[i]));
        }
        return max;
    }

    private void updateHeights(int[] heights, char[] cells) {
        for (int j = 0; j < heights.length; j++) {
            heights[j] = cells[j] == '0' ? 0 : heights[j] + 1;
        }
    }

    private int largestSquareArea(int[] heights,char[] cells) {
        int len = heights.length;
        int max = 0;
        int k,value,wide = 0;

        for (int r = 0; r < len; r++) {
            // 如果该位置没有高则直接跳过
            if (heights[r] == 0) {
                wide = 0;
                continue;
            }
            // 因为正方形要求的是高和宽一致，所以短板取决于最小值
            wide++;
            value = Math.min(heights[r],wide);
            k = r;
            // 保证数组不会溢出
            while (--k >= 0 && (heights[k] >= value || heights[k]*heights[k] > max)) {}
            value = Math.min(value,r-k);
            max = Math.max(max, value*value);
        }
        return max;
    }
}


//时间7 ms 击败 32.45%
//内存53 MB 击败 33.12%
class Solution {
    public int maximalSquare(char[][] matrix) {
        int maxSide = 0;
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return maxSide;
        }
        int rows = matrix.length, columns = matrix[0].length;
        int[][] dp = new int[rows][columns];
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < columns; j++) {
                if (matrix[i][j] == '1') {
                    if (i == 0 || j == 0) {
                        dp[i][j] = 1;
                    } else {
                        dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
                    }
                    maxSide = Math.max(maxSide, dp[i][j]);
                }
            }
        }
        int maxSquare = maxSide * maxSide;
        return maxSquare;
    }
}

//时间5 ms 击败 95.11%
//内存52.8 MB 击败 51.59%
class Solution {
    private int min(int a,int b,int c){
        return Math.min(a,Math.min(b,c));
    }

    public int maximalSquare(char[][] matrix) {
        if(matrix == null) return 0;

        int m = matrix.length;
        int n = matrix[0].length;
        //dp[i][j] 以matrix[i][j]为右下角的 全是1的正方形的最大边长 可以以左上角为研究对象 但是麻烦一些
        int[][] dp = new int[m][n];

        //先计算第一行 第一列的值 
        for(int i = 0;i<m;i++){
            dp[i][0]  = matrix[i][0] - '0';
        }

        for(int j = 0;j<n;j++){
            dp[0][j] = matrix[0][j] - '0';
        }

        for(int i = 1;i<m;i++){
            for(int j = 1;j<n;j++){
                //没必要用递归计算
                if(matrix[i][j]=='0'){
                    continue;
                }
                dp[i][j] = min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1;
            }
        }

        int maxLength = 0;
        for(int i = 0;i<m;i++){
            for(int j = 0;j<n;j++){
                maxLength = Math.max(maxLength,dp[i][j]);
            }
        }

        return maxLength*maxLength;
    }
}