230. 二叉搜索树中第K小的元素

题目：

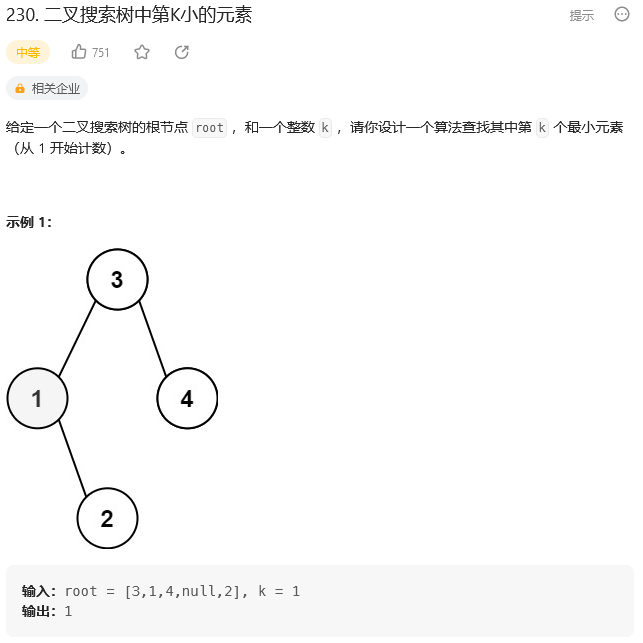
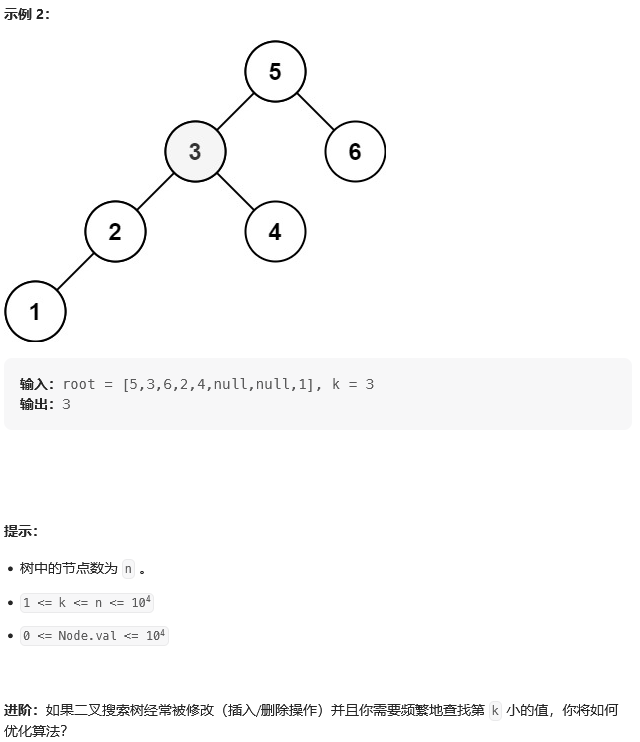
思路：

【1】常规的只查一次的话其实少不了遍历（最好是中序遍历，因为这样比较符合正常排好的顺序），遍历后需要弹出第K个位置就好

【2】如果是频繁的对某棵树进行查找的话（变更少或者不变更），那么最好是进行存储，用list存储，这样比那里一次但是根据下标就能快速找出想要的K值

【3】如果是频繁的对某棵树进行变更与查找（那么最好是做成平衡二叉树，可以参考优先队列的源码），然后其实依旧可以快速查找

代码展示：

【1】常规的只查一次的话

//时间0 ms 击败 100%
//内存42.8 MB 击败 70.40%
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int kthSmallest(TreeNode root, int k) {
        Deque<TreeNode> stack = new ArrayDeque<TreeNode>();
        while (root != null || !stack.isEmpty()) {
            while (root != null) {
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            --k;
            if (k == 0) {
                break;
            }
            root = root.right;
        }
        return root.val;
    }
}

 

【2】如果是频繁的对某棵树进行查找的话

//时间2 ms 击败 9.20%
//内存43 MB 击败 34.61%
//其实这种树转化成MAP记录树节点的方式我也不知好处在哪
//如果是不常变更的话用list存储会不会更好，这样拿出来的时间复杂度就是O(1)
//相反如果要变更的话其实这个MAP的数据也是需要对多个节点进行变更
class Solution {
    public int kthSmallest(TreeNode root, int k) {
        MyBst bst = new MyBst(root);
        return bst.kthSmallest(k);
    }
}

class MyBst {
    TreeNode root;
    Map<TreeNode, Integer> nodeNum;

    public MyBst(TreeNode root) {
        this.root = root;
        this.nodeNum = new HashMap<TreeNode, Integer>();
        countNodeNum(root);
    }

    // 返回二叉搜索树中第k小的元素
    public int kthSmallest(int k) {
        TreeNode node = root;
        while (node != null) {
            int left = getNodeNum(node.left);
            if (left < k - 1) {
                node = node.right;
                k -= left + 1;
            } else if (left == k - 1) {
                break;
            } else {
                node = node.left;
            }
        }
        return node.val;
    }

    // 统计以node为根结点的子树的结点数
    private int countNodeNum(TreeNode node) {
        if (node == null) {
            return 0;
        }
        nodeNum.put(node, 1 + countNodeNum(node.left) + countNodeNum(node.right));
        return nodeNum.get(node);
    }

    // 获取以node为根结点的子树的结点数
    private int getNodeNum(TreeNode node) {
        return nodeNum.getOrDefault(node, 0);
    }
}

 

【3】如果是频繁的对某棵树进行变更与查找

//时间47 ms 击败 3.9%
//内存42.8 MB 击败 67.14%
class Solution {
    public int kthSmallest(TreeNode root, int k) {
        // 中序遍历生成数值列表
        List<Integer> inorderList = new ArrayList<Integer>();
        inorder(root, inorderList);

        // 构造平衡二叉搜索树
        AVL avl = new AVL(inorderList);

        // 模拟1000次插入和删除操作
        int[] randomNums = new int[1000];
        Random random = new Random();
        for (int i = 0; i < 1000; ++i) {
            randomNums[i] = random.nextInt(10001);
            avl.insert(randomNums[i]);
        }
        shuffle(randomNums); // 列表乱序
        for (int i = 0; i < 1000; ++i) {
            avl.delete(randomNums[i]);
        }

        return avl.kthSmallest(k);
    }

    private void inorder(TreeNode node, List<Integer> inorderList) {
        if (node.left != null) {
            inorder(node.left, inorderList);
        }
        inorderList.add(node.val);
        if (node.right != null) {
            inorder(node.right, inorderList);
        }
    }

    private void shuffle(int[] arr) {
        Random random = new Random();
        int length = arr.length;
        for (int i = 0; i < length; i++) {
            int randIndex = random.nextInt(length);
            int temp = arr[i];
            arr[i] = arr[randIndex];
            arr[randIndex] = temp;
        }
    }
}

// 平衡二叉搜索树（AVL树）：允许重复值
class AVL {
    Node root;

    // 平衡二叉搜索树结点
    class Node {
        int val;
        Node parent;
        Node left;
        Node right;
        int size;
        int height;

        public Node(int val) {
            this(val, null);
        }

        public Node(int val, Node parent) {
            this(val, parent, null, null);
        }

        public Node(int val, Node parent, Node left, Node right) {
            this.val = val;
            this.parent = parent;
            this.left = left;
            this.right = right;
            this.height = 0; // 结点高度：以node为根节点的子树的高度（高度定义：叶结点的高度是0）
            this.size = 1; // 结点元素数：以node为根节点的子树的节点总数
        }
    }

    public AVL(List<Integer> vals) {
        if (vals != null) {
            this.root = build(vals, 0, vals.size() - 1, null);
        }
    }

    // 根据vals[l:r]构造平衡二叉搜索树 -> 返回根结点
    private Node build(List<Integer> vals, int l, int r, Node parent) {
        int m = (l + r) >> 1;
        Node node = new Node(vals.get(m), parent);
        if (l <= m - 1) {
            node.left = build(vals, l, m - 1, node);
        }
        if (m + 1 <= r) {
            node.right = build(vals, m + 1, r, node);
        }
        recompute(node);
        return node;
    }

    // 返回二叉搜索树中第k小的元素
    public int kthSmallest(int k) {
        Node node = root;
        while (node != null) {
            int left = getSize(node.left);
            if (left < k - 1) {
                node = node.right;
                k -= left + 1;
            } else if (left == k - 1) {
                break;
            } else {
                node = node.left;
            }
        }
        return node.val;
    }

    public void insert(int v) {
        if (root == null) {
            root = new Node(v);
        } else {
            // 计算新结点的添加位置
            Node node = subtreeSearch(root, v);
            boolean isAddLeft = v <= node.val; // 是否将新结点添加到node的左子结点
            if (node.val == v) { // 如果值为v的结点已存在
                if (node.left != null) { // 值为v的结点存在左子结点，则添加到其左子树的最右侧
                    node = subtreeLast(node.left);
                    isAddLeft = false;
                } else { // 值为v的结点不存在左子结点，则添加到其左子结点
                    isAddLeft = true;
                }
            }

            // 添加新结点
            Node leaf = new Node(v, node);
            if (isAddLeft) {
                node.left = leaf;
            } else {
                node.right = leaf;
            }

            rebalance(leaf);
        }
    }

    // 删除值为v的结点 -> 返回是否成功删除结点
    public boolean delete(int v) {
        if (root == null) {
            return false;
        }

        Node node = subtreeSearch(root, v);
        if (node.val != v) { // 没有找到需要删除的结点
            return false;
        }

        // 处理当前结点既有左子树也有右子树的情况
        // 若左子树比右子树高度低，则将当前结点替换为右子树最左侧的结点，并移除右子树最左侧的结点
        // 若右子树比左子树高度低，则将当前结点替换为左子树最右侧的结点，并移除左子树最右侧的结点
        if (node.left != null && node.right != null) {
            Node replacement = null;
            if (node.left.height <= node.right.height) {
                replacement = subtreeFirst(node.right);
            } else {
                replacement = subtreeLast(node.left);
            }
            node.val = replacement.val;
            node = replacement;
        }

        Node parent = node.parent;
        delete(node);
        rebalance(parent);
        return true;
    }

    // 删除结点p并用它的子结点代替它，结点p至多只能有1个子结点
    private void delete(Node node) {
        if (node.left != null && node.right != null) {
            return;
            // throw new Exception("Node has two children");
        }
        Node child = node.left != null ? node.left : node.right;
        if (child != null) {
            child.parent = node.parent;
        }
        if (node == root) {
            root = child;
        } else {
            Node parent = node.parent;
            if (node == parent.left) {
                parent.left = child;
            } else {
                parent.right = child;
            }
        }
        node.parent = node;
    }

    // 在以node为根结点的子树中搜索值为v的结点，如果没有值为v的结点，则返回值为v的结点应该在的位置的父结点
    private Node subtreeSearch(Node node, int v) {
        if (node.val < v && node.right != null) {
            return subtreeSearch(node.right, v);
        } else if (node.val > v && node.left != null) {
            return subtreeSearch(node.left, v);
        } else {
            return node;
        }
    }

    // 重新计算node结点的高度和元素数
    private void recompute(Node node) {
        node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
        node.size = 1 + getSize(node.left) + getSize(node.right);
    }

    // 从node结点开始（含node结点）逐个向上重新平衡二叉树，并更新结点高度和元素数
    private void rebalance(Node node) {
        while (node != null) {
            int oldHeight = node.height, oldSize = node.size;
            if (!isBalanced(node)) {
                node = restructure(tallGrandchild(node));
                recompute(node.left);
                recompute(node.right);
            }
            recompute(node);
            if (node.height == oldHeight && node.size == oldSize) {
                node = null; // 如果结点高度和元素数都没有变化则不需要再继续向上调整
            } else {
                node = node.parent;
            }
        }
    }

    // 判断node结点是否平衡
    private boolean isBalanced(Node node) {
        return Math.abs(getHeight(node.left) - getHeight(node.right)) <= 1;
    }

    // 获取node结点更高的子树
    private Node tallChild(Node node) {
        if (getHeight(node.left) > getHeight(node.right)) {
            return node.left;
        } else {
            return node.right;
        }
    }

    // 获取node结点更高的子树中的更高的子树
    private Node tallGrandchild(Node node) {
        Node child = tallChild(node);
        return tallChild(child);
    }

    // 重新连接父结点和子结点（子结点允许为空）
    private static void relink(Node parent, Node child, boolean isLeft) {
        if (isLeft) {
            parent.left = child;
        } else {
            parent.right = child;
        }
        if (child != null) {
            child.parent = parent;
        }
    }

    // 旋转操作
    private void rotate(Node node) {
        Node parent = node.parent;
        Node grandparent = parent.parent;
        if (grandparent == null) {
            root = node;
            node.parent = null;
        } else {
            relink(grandparent, node, parent == grandparent.left);
        }

        if (node == parent.left) {
            relink(parent, node.right, true);
            relink(node, parent, false);
        } else {
            relink(parent, node.left, false);
            relink(node, parent, true);
        }
    }

    // trinode操作
    private Node restructure(Node node) {
        Node parent = node.parent;
        Node grandparent = parent.parent;

        if ((node == parent.right) == (parent == grandparent.right)) { // 处理需要一次旋转的情况
            rotate(parent);
            return parent;
        } else { // 处理需要两次旋转的情况：第1次旋转后即成为需要一次旋转的情况
            rotate(node);
            rotate(node);
            return node;
        }
    }

    // 返回以node为根结点的子树的第1个元素
    private static Node subtreeFirst(Node node) {
        while (node.left != null) {
            node = node.left;
        }
        return node;
    }

    // 返回以node为根结点的子树的最后1个元素
    private static Node subtreeLast(Node node) {
        while (node.right != null) {
            node = node.right;
        }
        return node;
    }

    // 获取以node为根结点的子树的高度
    private static int getHeight(Node node) {
        return node != null ? node.height : 0;
    }

    // 获取以node为根结点的子树的结点数
    private static int getSize(Node node) {
        return node != null ? node.size : 0;
    }
}