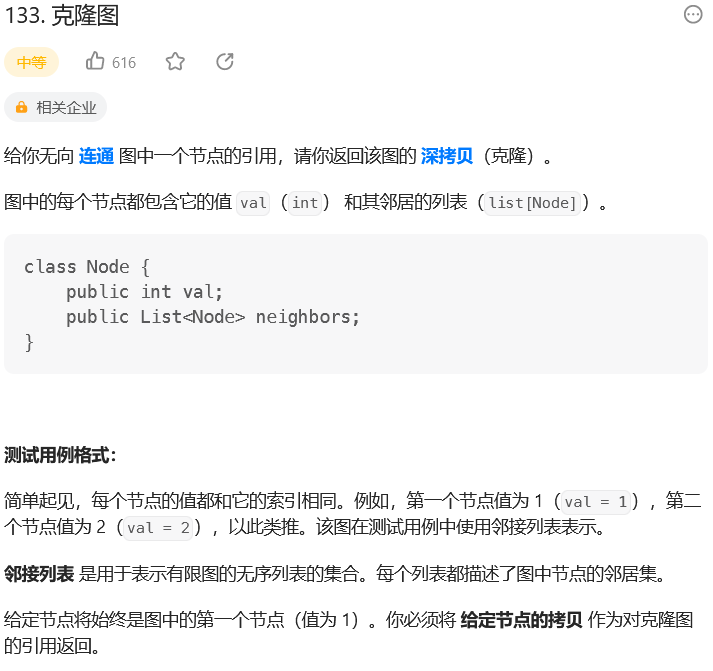
133. 克隆图

题目：

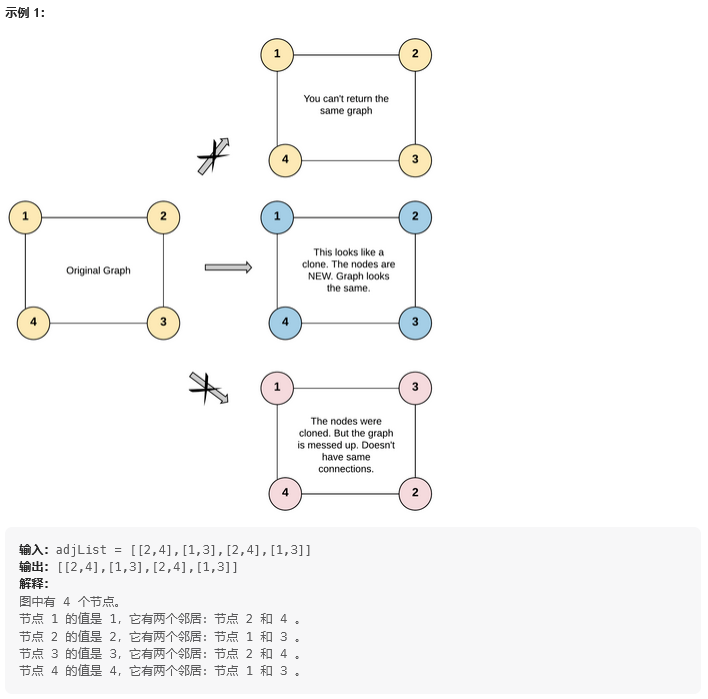
思路：

【1】所谓图克隆本质上就是另外开辟一块内存复制出跟给出的数据一致的内容

【2】既然是处理图那么最常用的便就是

思路一：DFS (深度遍历)

思路二：BFS (广度遍历)

辅助以字典相助

 

代码展示：

//深度搜索的方式
//时间23 ms 击败 99.95%
//内存40.8 MB 击败 74.80%
/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> neighbors;
    public Node() {
        val = 0;
        neighbors = new ArrayList<Node>();
    }
    public Node(int _val) {
        val = _val;
        neighbors = new ArrayList<Node>();
    }
    public Node(int _val, ArrayList<Node> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
}
*/

class Solution {
    public Node cloneGraph(Node node) {
        Map<Node, Node> lookup = new HashMap<>();
        return dfs(node, lookup);
    }

    private Node dfs(Node node, Map<Node,Node> lookup) {
        if (node == null) return null;

        if (lookup.containsKey(node)) return lookup.get(node);
        Node clone = new Node(node.val, new ArrayList<>());
        lookup.put(node, clone);
        for (Node n : node.neighbors)clone.neighbors.add(dfs(n,lookup));
        return clone;

    }
}

//时间24 ms 击败 74.75%
//内存40.7 MB 击败 81.60%
/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> neighbors;
    public Node() {
        val = 0;
        neighbors = new ArrayList<Node>();
    }
    public Node(int _val) {
        val = _val;
        neighbors = new ArrayList<Node>();
    }
    public Node(int _val, ArrayList<Node> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
}
*/

class Solution {
    private HashMap <Node, Node> visited = new HashMap <> ();
    public Node cloneGraph(Node node) {
        if (node == null) {
            return node;
        }

        // 如果该节点已经被访问过了，则直接从哈希表中取出对应的克隆节点返回
        if (visited.containsKey(node)) {
            return visited.get(node);
        }

        // 克隆节点，注意到为了深拷贝我们不会克隆它的邻居的列表
        Node cloneNode = new Node(node.val, new ArrayList());
        // 哈希表存储
        visited.put(node, cloneNode);

        // 遍历该节点的邻居并更新克隆节点的邻居列表
        for (Node neighbor: node.neighbors) {
            cloneNode.neighbors.add(cloneGraph(neighbor));
        }
        return cloneNode;
    }
}


//广度搜索的方式
//时间24 ms 击败 74.75%
//内存41 MB 击败 53.27%
/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> neighbors;
    public Node() {
        val = 0;
        neighbors = new ArrayList<Node>();
    }
    public Node(int _val) {
        val = _val;
        neighbors = new ArrayList<Node>();
    }
    public Node(int _val, ArrayList<Node> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
}
*/

class Solution {
    public Node cloneGraph(Node node) {
        if (node == null) {
            return node;
        }

        HashMap<Node, Node> visited = new HashMap();

        // 将题目给定的节点添加到队列
        LinkedList<Node> queue = new LinkedList<Node> ();
        queue.add(node);
        // 克隆第一个节点并存储到哈希表中
        visited.put(node, new Node(node.val, new ArrayList()));

        // 广度优先搜索
        while (!queue.isEmpty()) {
            // 取出队列的头节点
            Node n = queue.remove();
            // 遍历该节点的邻居
            for (Node neighbor: n.neighbors) {
                if (!visited.containsKey(neighbor)) {
                    // 如果没有被访问过，就克隆并存储在哈希表中
                    visited.put(neighbor, new Node(neighbor.val, new ArrayList()));
                    // 将邻居节点加入队列中
                    queue.add(neighbor);
                }
                // 更新当前节点的邻居列表
                visited.get(n).neighbors.add(visited.get(neighbor));
            }
        }

        return visited.get(node);
    }
}