149. 直线上最多的点数
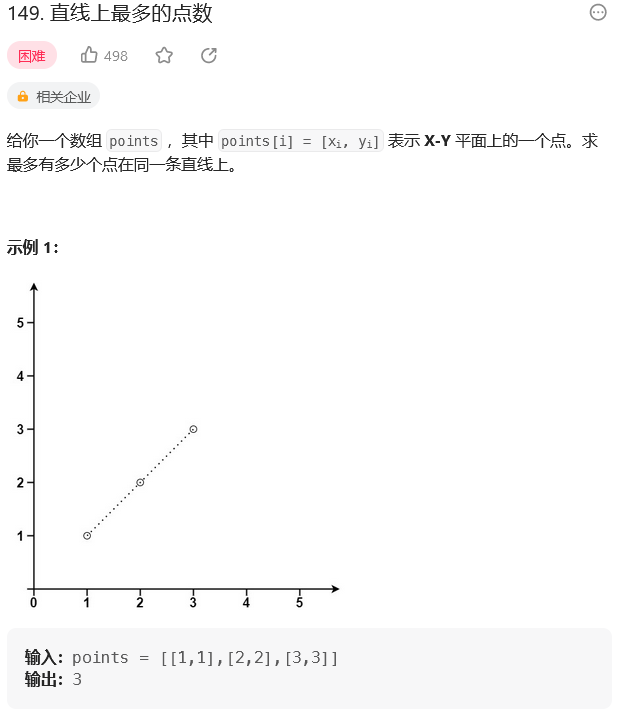
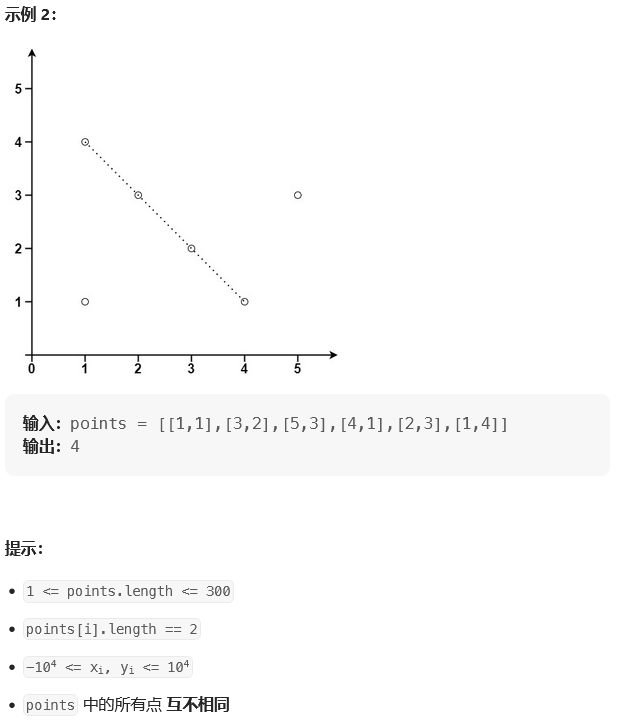
题目:
思路:
【1】本质上都是需要用到两点组成一条直线的公式 y+k*x = b,其中k为斜率,x和y为横纵坐标,b为常量值。
代码展示:
【1】暴力模拟的方式:
//时间7 ms 击败 99.36% //内存39.1 MB 击败 83.32% //时间复杂度:O(n^3)。 //空间复杂度:O(1),只用到了常量计算。 class Solution { public int maxPoints(int[][] points) { int n = points.length; // 基于两点确定一线的概念如果小于或等于2都算是在一条线上 if (n <= 2) return n; int ans = 0; // 根据数学公式 y+kx=b ,由两点确认参数k 和 b , // 便可以得到一条线的公式,如果点在公式内,则点在线内 // 所以逻辑是先基于两点确定一条线,然后判断其他点在不在这条线上 for (int i = 0; i < n; i++) { // 这个的意义何在(相当于截枝) // 一种是如果该点就算与剩下的其他点都能相连的个数都远比已存在的最大值小,也就没有必要进行下去了 // 一种是如果在该点之前的其他点已经存在能与大多数点(超过一半) if (ans >= n - i || ans > n / 2) { break; } for (int j = i + 1; j < n; j++) { // 先通过选取两点 , 存在 y1 + k*x1 = b , y2 + k*x2 = b // 斜率 k1 = -(y2-y1)/(x2-x1) int x1 = points[i][0], y1 = points[i][1], x2 = points[j][0], y2 = points[j][1]; int count = 2; // 再选取第三个点与第一个点组合成一条线 y + k*x = b,k2 = -(y-y1)/(x-x1) // 判断第三个点在不在确定的这条线上 , 如果在在则必然存在 k2 = k1 // 故 (y - y1) * (x2 - x1) == (y2 - y1) * (x - x1) for (int k = j + 1; k < n; k++) { int x = points[k][0], y = points[k][1]; if ((y - y1) * (x2 - x1) == (y2 - y1) * (x - x1)) count++; } ans = Math.max(ans, count); } } return ans; } }
【2】官方的思路:
//官方题解 //时间17 ms 击败 76.9% //内存42 MB 击败 41.97% //时间复杂度:O(n^2×logm),其中 n 为点的数量,m 为横纵坐标差的最大值。 //最坏情况下我们需要枚举所有 n 个点,枚举单个点过程中需要进行 O(n) 次最大公约数计算, //单次最大公约数计算的时间复杂度是 O(logm),因此总时间复杂度为 O(n^2×logm)。 //空间复杂度:O(n),其中 n 为点的数量。主要为哈希表的开销。 class Solution { public int maxPoints(int[][] points) { // 根据数学公式 y+kx=b ,由两点确认参数k 和 b , // 便可以得到一条线的公式,如果点在公式内,则点在线内 int n = points.length; // 基于两点确定一线的概念如果小于或等于2都算是在一条线上 if (n <= 2) return n; int ret = 0; for (int i = 0; i < n; i++) { // 这个的意义何在(相当于截枝) // 一种是如果该点就算与剩下的其他点都能相连的个数都远比已存在的最大值小,也就没有必要进行下去了 // 一种是如果在该点之前的其他点已经存在能与大多数点(超过一半) if (ret >= n - i || ret > n / 2) { break; } Map<Integer, Integer> map = new HashMap<Integer, Integer>(); for (int j = i + 1; j < n; j++) { int x = points[i][0] - points[j][0]; int y = points[i][1] - points[j][1]; if (x == 0) { // 特殊情况竖线 y = 1; } else if (y == 0) { // 特殊情况横线 x = 1; } else { if (y < 0) { x = -x; y = -y; } int gcdXY = gcd(Math.abs(x), Math.abs(y)); x /= gcdXY; y /= gcdXY; } int key = y + x * 20001; // 斜率相同的点数加1 map.put(key, map.getOrDefault(key, 0) + 1); } int maxn = 0; // 对应的因为是存放于map中需要遍历一下 for (Map.Entry<Integer, Integer> entry: map.entrySet()) { int num = entry.getValue(); maxn = Math.max(maxn, num + 1); } //然后保存最大值 ret = Math.max(ret, maxn); } return ret; } public int gcd(int a, int b) { return b != 0 ? gcd(b, a % b) : a; } } //简化一下写的方式 // 其实会发现大量的求公约数的循环会导致消耗的时间增多 //时间33 ms 击败 28.16% //内存43.4 MB 击败 8.29% class Solution { public int maxPoints(int[][] ps) { int n = ps.length; int ans = 0; for (int i = 0; i < n; i++) { // 这个的意义何在(相当于截枝) // 一种是如果该点就算与剩下的其他点都能相连的个数都远比已存在的最大值小,也就没有必要进行下去了 // 一种是如果在该点之前的其他点已经存在能与大多数点(超过一半) if (ans >= n - i || ans > n / 2) { break; } Map<String, Integer> map = new HashMap<>(); // 由当前点 i 发出的直线所经过的最多点数量 int max = 0; for (int j = i + 1; j < n; j++) { int x1 = ps[i][0], y1 = ps[i][1], x2 = ps[j][0], y2 = ps[j][1]; int a = x1 - x2, b = y1 - y2; int k = gcd(a, b); String key = (a / k) + "_" + (b / k); map.put(key, map.getOrDefault(key, 0) + 1); max = Math.max(max, map.get(key)); } ans = Math.max(ans, max + 1); } return ans; } int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); } }
当然还有无脑的写法:
//时间21 ms 击败 48.3% //内存42.4 MB 击败 26.88% class Solution { public int maxPoints(int[][] points) { int n = points.length; int ans = 0; for (int i = 0; i < n; i++) { // 这个的意义何在(相当于截枝) // 一种是如果该点就算与剩下的其他点都能相连的个数都远比已存在的最大值小,也就没有必要进行下去了 // 一种是如果在该点之前的其他点已经存在能与大多数点(超过一半) if (ans >= n - i || ans > n / 2) { break; } Map<Double, Integer> map = new HashMap<>(); // 由当前点 i 发出的直线所经过的最多点数量 int max = 0; for (int j = i + 1; j < n; j++) { int x1 = points[i][0], y1 = points[i][1], x2 = points[j][0], y2 = points[j][1]; double a = x1 - x2, b = y1 - y2; // 首先是通过计算斜率来放入hash表中的(相同斜率的即为在同一条线) // 由于是采用double来计算 故 会存在 x = 0 或 y = 0的情况 // 由于分母不可以为0 ,那么 当分母为零的时候设置为 20010 (也就是在取值区间之外) // 由于 -10^4 <= xi, yi <= 10^4,所以 会存在 y1 - y2 = 20000 的情况 // 另外由于double 不会区分 -0.0 和 0.0 ,所以最后结果要采用 0 - key // 因为这样子处理 会把 -0.0 和 0.0 都置为 0 ,非零的情况也不过是 取反而已不影响结果 double key = a == 0 ? 20010 : 0 - (b / a); map.put(key, map.getOrDefault(key, 0) + 1); max = Math.max(max, map.get(key)); } ans = Math.max(ans, max + 1); } return ans; } }
优化的方式:
//时间4 ms 击败 100% //内存42.3 MB 击败 29.1% class Solution { public int maxPoints(int[][] points) { int n = points.length; if (n < 3) { return n; } int max = 2; // 这里同样是采用 double来作为斜率的统计 for (int i = 0; i < n; i++) { max = Math.max(max, getMax(points[i][0], points[i][1], i, points)); } return max; } public int getMax(int x , int y, int i, int[][] points) { int n = points.length; int max = 2; Map<Double, int[]> lines = new HashMap<>(n - i - 1, 0.95f); for (int j = i + 1; j < n; j++) { Double slope = points[j][1] == y ? 0.0 : points[j][0] == x ? Double.POSITIVE_INFINITY : (double) (points[j][1] - y) / (points[j][0] - x); // 至于这里为什么采用int 数组对象 (是为了避免往map里面的put操作,而是用get取出后直接修改) // 因为存的是引用,所以修改后引用指向的那块内存其实也是修改了的 int[] occurrences = lines.get(slope); if (occurrences == null) { lines.put(slope, new int[]{2}); } else { max = Math.max(max, ++occurrences[0]); } } return max; } }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号