201. 数字范围按位与

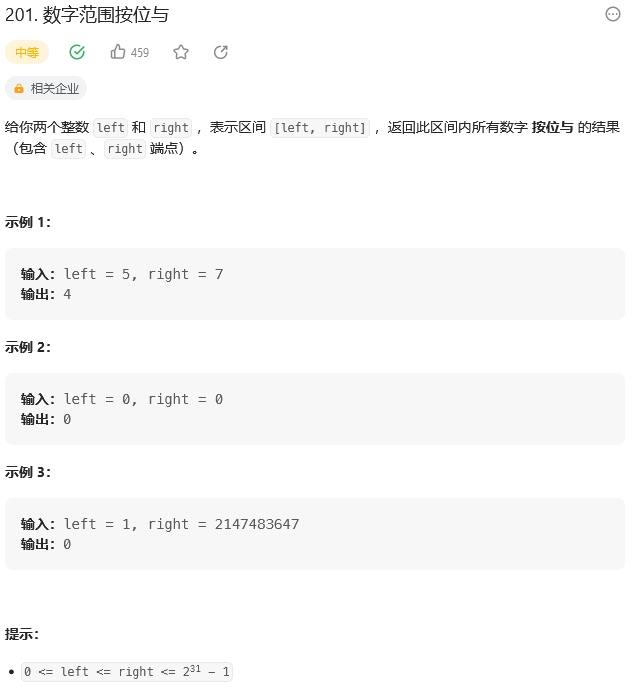
题目：

思路：

【0】虽说是按位与的结果，但是本质上是求这些数的二进制公共前缀的部分

值为：5 二进制为：101
值为：6 二进制为：110
值为：7 二进制为：111
值为：8 二进制为：1000
值为：9 二进制为：1001
值为：10 二进制为：1010
值为：11 二进制为：1011
值为：12 二进制为：1100

如 5-7 公共部分就是100 即 4
但 5-8 公共部分就是0000 即 0 
（因为8存在第四位是1，但其他数的是0，故也是0）
（而8的后三位是0会导致，其他数与之相与也会变为0）
重点在于 按位与 需要 1&1=1 
所以只需要根据两个边界值就可以知道两个区间的数值相与的结果了

【1】模拟 

【2】位移

这是由于因为变成了找最大公共前缀，两个边界值相差是最大的
所以通过不断去除掉不相等的部分
（一般一个值增长到另一个值，都是末尾的进制位变化【从而导致进位影响到高位】）
所以去除掉末尾直至到两数相等的情况
如
值为：6 二进制为：00000000000000000000000000000110
值为：7 二进制为：00000000000000000000000000000111
公共部分为0000000000000000000000000000011（0 ，少掉的末尾1个0）= 6
又如
值为：7 二进制为：00000000000000000000000000000111
值为：8 二进制为：00000000000000000000000000001000
公共部分为0000000000000000000000000000（0000 ，少掉的末尾4个0） = 0

 

【3】Brian Kernighan 算法（这种同样是移除末尾的1）

代码展示：

【1】模拟 

//时间1226 ms 击败 5%
//内存41.6 MB 击败 32.75%
class Solution {
    public int rangeBitwiseAnd(int left, int right) {
        // 确保小的值放在left指针上
        if (left > right){
            return rangeBitwiseAnd(right,left);
        }
        
        int res = left;
        while (left < right){
            // 区间内的值全部相与
            res &= ++left;
            // 这里如果不加容易出现超时限制
            // 而且能起到截断的作用，因为0&x=0，无论x为何值，故直接返回即可
            if (res == 0) return 0;
        }
        return res;
    }
}

【2】位移

//时间3 ms 击败 100%
//内存41.5 MB 击败 44.49%
class Solution {
    public int rangeBitwiseAnd(int left, int right) {
        int shift = 0;
        // 找到公共前缀
        while (left < right) {
            left >>= 1;
            right >>= 1;
            ++shift;
        }
        return left << shift;
    }
}

【3】Brian Kernighan 算法

//时间3 ms 击败 100%
//内存41.9 MB 击败 6.27%
class Solution {
    public int rangeBitwiseAnd(int left, int right) {
        while (left < right) {
            // 抹去最右边的 1
            right = right & (right - 1);
        }
        return right;
    }
}